2.6.4.Метод оценки и пересмотра планов (перт)

Методы, которые мы уже рассмотрели в этом разделе, исходя из того, что продолжительность всех действий по проекту известна. На практике это вещь невозможная, и продолжительность можно только спрогнозировать, исходя из прошлого опыта. Использование ПЕРТ позволяет проводить более сложный анализ поставленной задачи. Этот метод заключается в определе­нии крайних сроков каждого действия и их наиболее вероятной продолжи­тельности.

Например, в таблице ниже дана наиболее вероятная, максимально воз­можная и минимально возможная продолжительность некоего действия. Макси­мальная оценка часто называется пессимистической, а минимальная -опти­мистической.

Действие	Оценочная продолжительность (дней)
	Наиболее вероятная	Оптимистическая	Пессимистическая
А	19	16	28

Ожидаемую (среднюю) продолжительность этого действия можно оценить как взвешенное среднее трех оценочных показателей следующим образом:

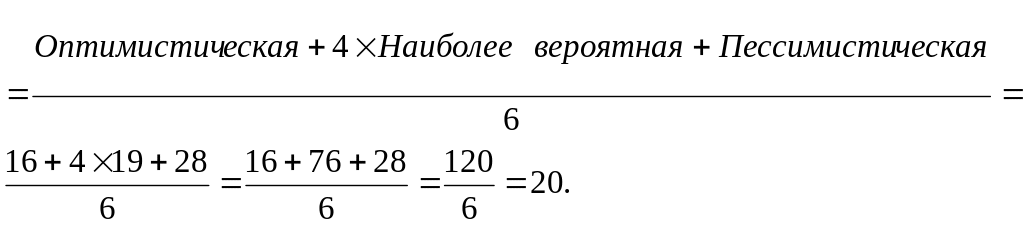
Отсюда ожидаемая продолжительность этого действия – 20 дней. Это зна­чение будет использоваться при анализе с помощью сетевого графика.

Далее, целесообразно оценить показатель разброса (среднеквадратическое отклонение) с тем, чтобы проанализировать возможный разброс в продолжи­тельности всего проекта. Методы нормального распределения, описанные в разделе 3, позволяют оценить среднеквадратическое отклонение исходя из диапа­зона: 99,8% доверительные пределы равняются приблизительно , что по­казано графике на рис. 2.19. Т. е. три среднеквадратических отклонения в любую из сторон от среднего фактически захватят все из значений распреде­ления.

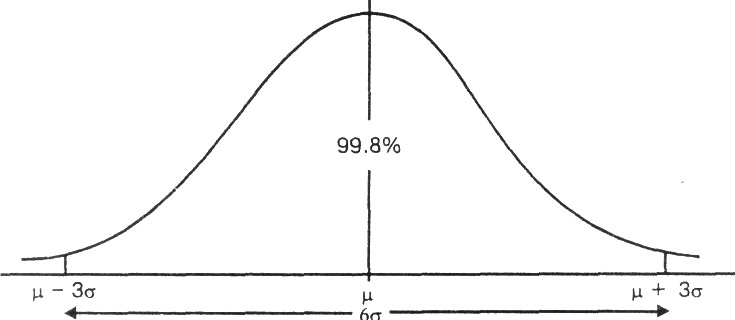
Рис. 2.19. Доверительные пределы нормального распределения

Отсюда, разница между максимальным и минимальным значениями в этом распределении составляет приблизительно 6 среднеквадратических отклонений. Поэтому разумная оценка среднеквадратического отклонения определяется следующим образом:

,

Т. е. .

Что является определением среднеквадратического отклонения по формуле:

.

В нашем примере это означает, что среднеквадратическое отклонение действия А (обозначается как А) составляет:

;

.

Итак, действие А имеет ожидаемую продолжительность в 20 дней со среднеквадратическим отклонением в 2 дня. Такого рода анализ можно провести по каждому действию, предусмотренному проектом.

Ожидаемая продолжительность и среднеквадратическое отклонение про­должительности всего проекта могут быть получены путем сочетания ожидае­мых значений и среднеквадратических отклонений всех критических действий. Так, если действия А, Б и В являются критическими с ожидаемыми значениями Е_А, Е_Б и Е_В и среднеквадратическими отклонениями , и , то общая продолжительность проекта определяется следующим образом:

Ожидаемая продолжительность проекта = Е_А + Е_Б + Е_В.

Отклонение в продолжительности = .

Среднеквадратическое отклонение = .

В следующем разделе приведены примеры использования этих методов в управлении проектом.

Определение. ПЕРТ использует понятия неопределенности при оценке сроков и вероятностей при определении ожидаемой продолжительности действий в рамках проекта.

Пример 1

Рассмотрим следующий перечень действий:

Работа	Очередность	Оценочная продолжительность (дней)
		Наиболее вероятная (НВ)	Оптимисти- ческая (О)	Пессимисти- ческая (Р)
А	-	9	8	16
Б	А	8	7	9
В	-	4	3	5
Г	В	5	5	5
Д	В	8	7	15
Е	Д	3	2	4

Ожидаемая продолжительность этих действий рассчитывается следующим образом.

Работа А: ожидаемая продолжительность = (8 + 4 9+ 16)/6 = 60/6 = 10 дней.

Б: ожидаемая продолжительность = (7 + 4 8 + 9)/6 = 8 дней.

В: ожидаемая продолжительность = (3 + 4 4 + 5)/6 = 4 дня.

Г: ожидаемая продолжительность =(5 + 4 5 + 5)/6 = 5 дней.

Д: ожидаемая продолжительность = (7 + 4 8+ 15)/6 = 9 дней.

Е: ожидаемая продолжительность =(2 + 4 3 + 4)/6 = 3 дня.

Сетевой график этих действий с их ожидаемой продолжительностью представлен на рис. 2.20. Как видно из графика, критические работы - А и Б.

Для работы А:

Ожидаемая продолжительность = 10 дней.

Среднеквадратическое отклонение = =1,33 дня.

Для работы Б:

Ожидаемая продолжительность = 8 дней.

Среднеквадратическое отклонение = = 0,33 дня.

Ожидаемая продолжительность проекта: 10 + 8 = 18 дней со среднеквадратическим отклонением:

= 1,37 дня.

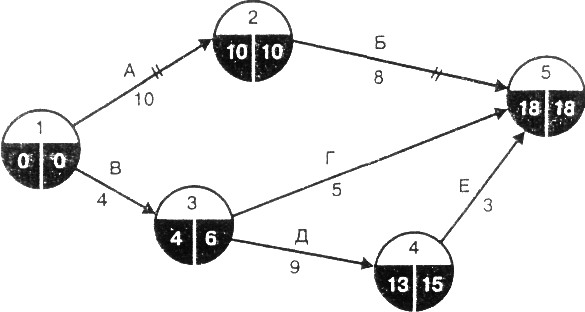
Рис. 2.20. Сетевой график с ожидаемой продолжительностью

Эти значения можно использовать при дальнейшем анализе проекта. На­пример, можно определить вероятность того, что продолжительность проекта превысит 20 дней. При условии, что продолжительность проекта нормально распределена, это можно сделать следующим образом:

Средняя продолжительность проекта – 18 дней.

Среднеквадратическое отклонение продолжительности проекта – 1.37 дня.

Распределение всей продолжительности проекта показано на рис. 2.21.

Вероятность того, что продолжительность составит более 20 дней – выде­ленный участок.

А теперь для определения этого участка мы вычислим нормированную случайную величину:

С помощью таблиц нормального распределения находим, что выделенный участок – 0,072.

Это указывает на то, что имеется 7,2%-я вероятность того, что продол­жительность проекта превысит 20 дней. Далее можно провести анализ возмож­ных колебаний продолжительности всего проекта.

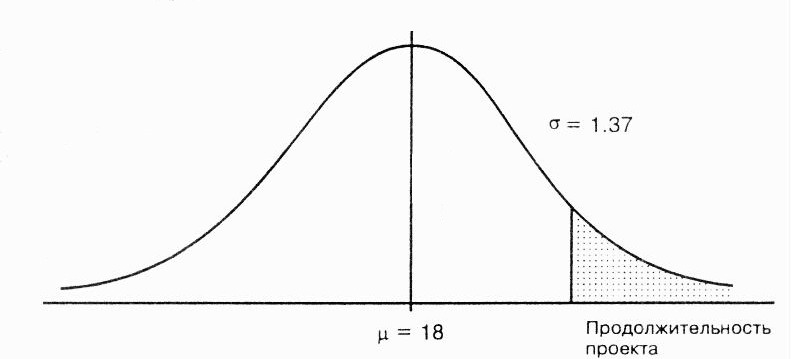
Рис. 2.21. Вероятность того, что продолжительность проекта превысит