Іі. Приклади розв’язку задач

1.102. В трикутнику АВС сторона АВ точками М і N розділена на три рівні частини: . Знайти вектор , якщо .

 Маємо . Звідси,

Отже , тоді . ▲

1.103. В трикутнику АВС пряма АМ є бісектрисою кута ВАС, причому точка М лежить на стороні ВС. Знайти , якщо .

 Маємо . Із властивості бісектриси внутрішнього кута трикутника випливає, що , тобто .

Звідси одержуємо .

Оскільки , тоді . ▲

1.104. Задані точки А(1, 2, 3) і В(3, -4, 6). Знайти довжину, напрямок і норму вектора .

 Проекціями вектора на осі координат є різниця відповідних координат точок В і А: а_х=3-1=2, а_у=-4-2=-6, a_z=6-3=3. Звідси . Знайдемо довжину вектора

Шуканий одиничний вектор має вигляд . ▲

1.105. Заданий трикутник: А(1, 1, 1), В(5, 1,-2), С(7, 9, 1). Знайти координати точки D перетину бісектриси кута А зі стороною СВ.

 Знайдемо довжини сторін трикутника, що утворюють кут А:

Звідси , оскільки бісектриса ділить сторону СВ на частини, пропорційні прилеглим сторонам. Таким чином,

шукана точка D(17/3, 11/3, -7). ▲

1.106. На осі Ох знайти точку, рівновіддалену від точок А(2; -4; 5) і В(-3; 2; 7).

 Нехай М – шукана точка. Тоді . Оскільки точка М лежить на осі х, то її координати (х, 0, 0).

Отже (x-2)²+41=(x+3)²+53; або 10х=-17, тобто х=-1,7.

Звідси М(-1,7; 0; 0). ▲

1.107. Задані вектори .

Обчислити скалярні добутки:

 Знаходимо:

▲

1.108. Обчислити, при якому значенні вектори взаємно перпендикулярні.

 Знаходимо скалярний добуток цих векторів: ; Оскільки , тоді .

Звідси . ▲

1.109. Обчислити кут між векторами .

 Оскільки , тоді

Маємо

. Отже , і . ▲

1.110. Знайти вектор , який перпендикулярний до векторів та відповідає умові .

 Оскільки , тоді . Шуканий вектор має координати .

Отже

Розв’язуючи одержану систему, маємо

тобто . ▲

1.111. Задані вектори . Знайти координати векторних добутків:

 Знаходимо:

▲

1.112. Задані вершини трикутника А(1; 2; 0), В(3; 0; -3) і С(5; 2; 6).

Обчислити його площу.

 Знаходимо вектори і .

Площа трикутника АВС дорівнює половині площі паралелограма, побудованого на векторах і , а тому знаходимо векторний добуток цих векторів

Звідси

▲

1.113. Обчислити площу паралелограма, побудованого на векторах , якщо .

 Маємо

(оскільки )

Звідси ▲

1.114. Знайти мішаний добуток векторів

.

 ▲

1.115. Знайти об’єм трикутної піраміди з вершинами А(-1; 0; 2), В(2; 1; 1), С(3; 0; -1), D(3; 2; 2).

 Знайдемо вектори , які співпадають з ребрами піраміди і сходяться у вершині А: . Знаходимо мішаний добуток цих векторів:

Оскільки об’єм піраміди дорівнює паралелепіпеда (рис.14), побудованого на векторах , тоді

▲

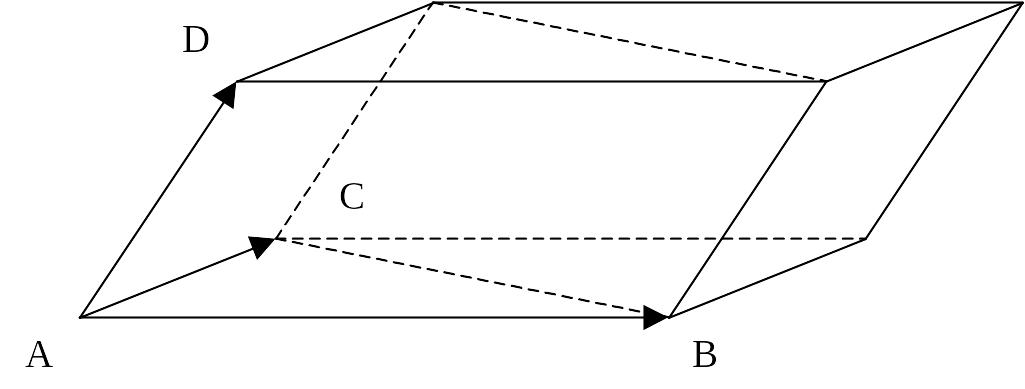
Рис.14

1.116. Показати, що вектори компланарні.

 Знаходимо мішаний добуток векторів

Оскільки , тоді задані вектори компланарні. ▲

77