§7 Векторний добуток векторів

_{Визначення. Векторним добутком двох векторів називається третій вектор, який має довжину, чисельно рівну площі паралелограма, що побудований на заданих векторах, перпендикулярний площині цих векторів і утворює з впорядкованою парою заданих векторів праву трійку.}

Позначається векторний добуток заданих векторів і символом (іноді позначають .

Оскільки площа паралелограма, побудованого на векторах і , дорівнює добутку довжини цих векторів і синуса кута між ними, то

(1)

Вкажемо на основні властивості векторного добутку векторів. Відмітимо передусім, що

₍₂₎

_{Дійсно, нехай}

_{Оскільки}

і

Вектори і перпендикулярні одній і тій же площині (площина, визначена векторами і ). Вектори , , утворюють праву трійку. Праву ж трійку утворюють і вектори , , `, тому вектори і мають однакові довжини, перпендикулярні одній і тій же площині і направлені в протилежні сторони. Це означає, що . Отже, при перестановці векторів, що перемножуються, напрямок векторного добутку змінюється на протилежний, а довжина не змінюється.

Можна довести, що векторний добуток двох векторів має сполучну властивість по відношенню до третього – скалярного – співмножника.

(3)

_{і має розподільчу властивість:}

(4)

_{Із визначення векторного добутку векторів випливає, що векторний добуток колінеарних векторів є завжди нульовий вектор. Зокрема, завжди}

_.

_{Оскільки вектори , , взаємно перпендикулярні, мають одиничні довжини і утворюють праву трійку, то}

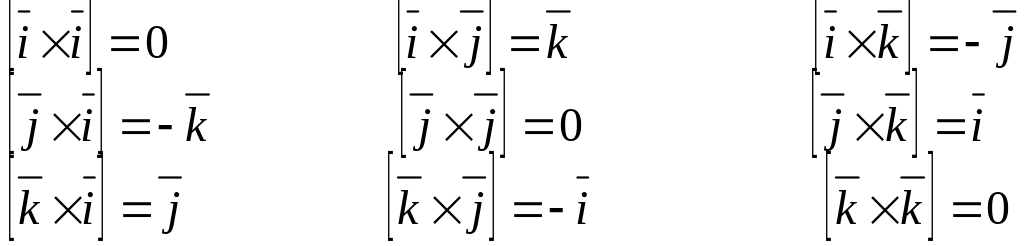₍₅₎

_{Використовуючи розподільчу і сполучну по відношенню до скалярного множника властивості векторного добутку, можна отримати формули для обчислення векторного добутку векторів, заданих шляхом розкладу по ортонормованому базису:}

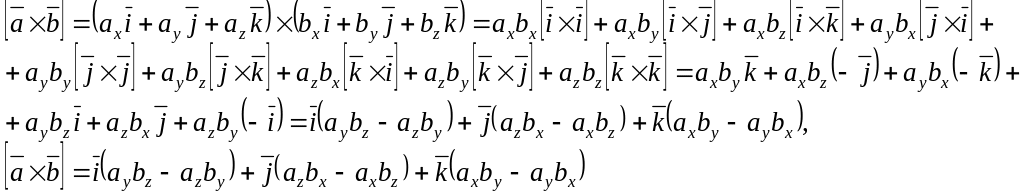₍₆₎

_{Важливою геометричною задачею, яка розв’язується з допомогою введеної операції, є обчислення площини трикутника по координатах його вершин.}

_{Нехай задані координати вершин трикутника А, В, С. Знаючи їх, знаходимо і . Площа трикутника АВС дорівнює половині площі паралелограма, побудованого на векторах і . Отже,}

₍₇₎

Приклад. А(1, -2,0); В(2, 1, -1); С(0, 3, 1). Знайти _.

_{Розв’язок}

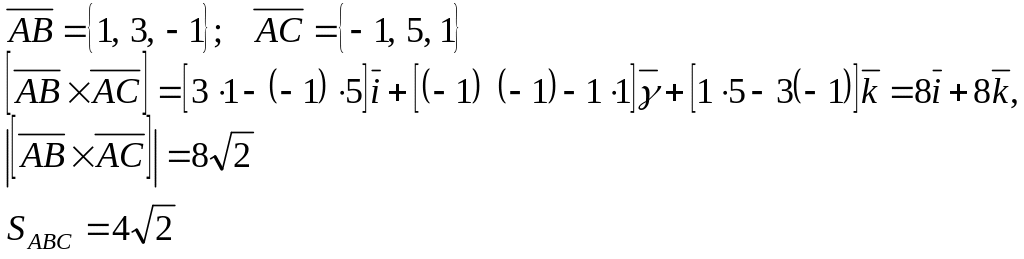
_{Нарешті, формулу для обчислення векторного добутку векторів (6) зручніше записувати через визначник}

_(8),

_{розкладаючи який по елементах першого рядка, отримаємо формулу (6).}

§8 Мішаний добуток векторів

Оскільки векторний добуток векторів і є вектор, то можливо розглядати і скалярний добуток вектора на і векторний добуток на . В нашому курсі ми розглянемо тільки перший із цих добутків.

Визначення. Скалярний добуток вектора на векторний добуток векторів і називається мішаним добутком векторів , , .

Отже, мішаним добутком векторів , і є вираз і представляє собою, очевидно, скаляр.

З‘ясуємо геометричний зміст введеного поняття. Нехай точка О є загальний початок трьох некомпланарних векторів , , .

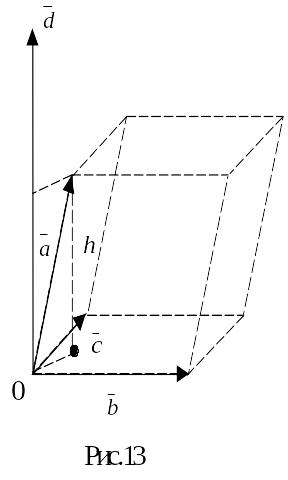
Побудуємо на заданих векторах паралелепіпед (рис.13) і знайдемо вектор . Із визначення скалярного добутку векторів, отримаємо

Але оскільки вектор перпендикулярний площині векторів і , то проекція вектора на вісь, направлену по вектору , або дорівнює висоті паралелепіпеда, якщо ця проекція додатна (тобто, якщо вектори , , утворюють праву трійку), або дорівнює висоті, взятій зі знаком мінус, якщо ця проекція від‘ємна (тобто, якщо три заданих вектора утворюють ліву трійку).

Отже, мішаний добуток трьох векторів дорівнює об‘єму паралелепіпеда, побудованого на цих векторах, якщо вони утворюють праву трійку, і дорівнює об‘єму паралелепіпеда, взятому зі знаком мінус, якщо вектори утворюють ліву трійку.

Якщо у вибраній трійці їх переставити, то паралелепіпед, побудований на цих векторах, очевидно, не зміниться. Зокрема, не зміниться і абсолютна величина мішаного добутку. Легко відмітити, що при круговій перестановці векторів права трійка векторів залишається правою, а ліва лівою. Тому при круговій перестановці векторів мішаний добуток векторів не змінюється.

Отже,

(1)

Якщо вектори задані своїми координатами в ортонормованому базисі , , :

,

Якщо задані три вектора компланарні, то їх мішаний добуток, очевидно, дорівнює нулю. Навпаки, якщо мішаний добуток трьох векторів дорівнює нулю, то ці вектори обов’язково компланарні. Дійсно, якщо скалярний добуток векторів і дорівнює нулю, то вектор перпендикулярний вектору ; але перпендикулярний також площині векторів і . Таким чином вектор лежить в площині векторів і . Звідси, вектори , , компланарні.

Отже, рівність нулю мішаного добутку трьох векторів є необхідна і достатня умова їх компланарності.

Формулу (2) можна записати, використовуючи визначник третього порядку

(3),

розкладаючи який по елементах 1-го рядка, отримаємо формулу (2).