9.7.1 Исследование сигнала для оценки канала

Рассмотрим модель с полосой дискретного времени, в которой канал, в любое время вывода m, представлен ​заданным числом случайно изменяющихся волн, . Мы будем учиться оценивать эти волны путем передачи исследуемого сигнала, состоящего из известных значений входных сигналов. Приемник, знающий передаваемые сигналы, производит оценку волн. Эта процедура повторяется как минимум один раз для каждого интервала времени согласования.

Один простой (но не очень хороший) выбор для такого известного сигнала является использование ввода максимальной амплитуды, скажем a, в данную эпоху, скажем, эпоху 0, следующей нулевым входам на следующих эпох. Полученная последовательность подобна эпохам в отсутствии шума как . При наличии значений комплексного дискретного времени WGN, выход во времени от 0 до , равен

Разумная оценка k-ой волны канала, при условии равна

Принципы оценки похожи на принципы обнаружения. В обнаружении наблюдение (простое значение случайной переменной или вектора V) используется для выбора из возможных значений дискретной случайной переменной U (гипотеза). В оценке, значение вектора V используется для выбора из возможных значений непрерывной rv G. В обоих случаях истины или считаются известными и априорные вероятности или также приняты известными.

Оценка, как и обнаружение, связана с определением и реализацией соответствующих правил оценки из . Широко используется правило максимальной истины (ML). Выбирается оценка из значений , которая максимизирует . ML правило для оценки такое же, как и для обнаружения. Отметим, что оценка (9.65) является ML оценкой.

Другое широко используемое правило это правило минимальной среднеквадратичной ошибки (MMSE). MMSE правило выбирает оценку , которая является апостериорной вероятной плотностью для данных наблюдений . Во многих случаях, например, когда G и V являются совместно Гауссовскими, это означает такое же значение , которое максимизирует . Таким образом, MMSE правило, несколько похоже на MAP правило теории обнаружения.

Для обнаружения проблем, обычно выбирается ML правило, когда априорные вероятности в случае ML и MAP эквивалентны. Для оценки проблем, намного чаще выбирается ML, когда априорная вероятность плотности неизвестна. Когда априорная вероятность плотности известна, MMSE правило, обычно имеет меньшую среднеквадратичную ошибку оценки, чем ML правило.

В различных ситуациях обычно очень мало оснований для предположения определенной модели волн канала (хотя модели Рэлея и Райса часто имеют что-то особенное для обсуждения). Таким образом, оценка ML имеет более значительный смысл, и именно она обычно используется. Поскольку канал меняется очень медленно с течением времени, то разумно предположить, что измерение в (9,65) может быть использовано в любое время в течение данного интервала согласования.

Также можно повторить описанную выше процедуру несколько раз в течение одного времени согласования. Несколько измерений фильтрованных волн каждого канала, могут быть усреднены (совокупная оценка ML основывается на нескольких наблюдений).

Проблема с единственным импульсным подходом заключается в том, что пик ограничения обычно существует на входной последовательности; поэтому два метода накладываются для того, чтобы избежать чрезмерных помех на другие каналы, а также для упрощения реализации. Если площадь этого пика ограничения меньше, чем энергия ограничения на символ, то длинная последовательность ввода с равной энергией в каждом символе позволит использовать гораздо больше энергии сигнала для измерения, чем единый импульсный подход.

Как видно в дальнейшем, этот подход будет получать более точные оценки ответа канала, чем единый импульсный подход.

Использование заранее установленного диаметрально противоположного псевдо-шума (PN) входной последовательности является хорошим способом выполнения измерений канала с такой равномерно распределенной энергией. Компоненты из выбраны так, чтобы быть ±a и обладали важным свойством: корреляционная функция от аппроксимирует импульс. То есть, последовательность выбрана для выполнения:

где принимается равным 0 вне интервала [1, n]. Для длинных PN последовательностей ошибка в этой аппроксимации может быть рассмотрена как дополнительный, но незначительный шум. Реализация таких векторов (в двоичной, а не диаметрально противоположной форме) обсуждается в конце этого пункта.

Почти очевидны возможности выбора , такой чтобы быть диаметрально противоположной PN последовательностью, выбрав её комплексной с диаметрально противоположной действительной и мнимой частями, то есть, получив 4-QAM последовательность. Выбирая действительную и мнимую части диаметрально противоположными PN последовательностями, а также аппроксимируя к некоррелированным, (9.66) становится

QAM форма распространяет входящую измеренную энергию в два раза больше, чем степеней свободы для данных n единиц времени, и, таким образом, обычно выгоднее. Обе, диаметрально-противоположная и 4-QAM формы, а также бинарная версия диаметрально противоположной формы, называются PN последовательностями.

Форма QAM, предполагаемая в дальнейшем, но с одним отличием между (9.66) и (9.67) это фактор 2 в ковариации. Для простоты также предполагается, что равенство (9.66) выполняется.

Условие (9.67) (с равенством) утверждает, что является ортогональным к каждому из своих сдвигов во времени. Это условие может быть выражено посредством определения фильтра согласования последовательности к последовательности , где .

То есть, является комплексно сопряженной к обратной во времени. Свертывание и так что . Ковариационное условие (9.67) (с равенством) тогда эквивалентно свертываемому состоянию,

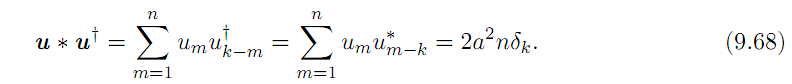
Пусть комплексные значения rv , будут значениями k-ой волны канала во времени m. Выходной канал в момент m и входной последовательностью (до добавления шума) является свертыванием:

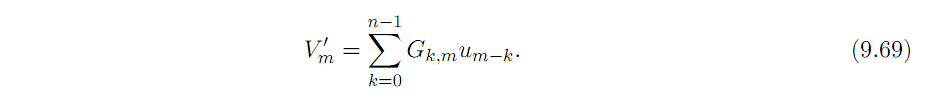С равной нулю вне интервала [1, n] и бесшумной выходной последовательностью равной нулю вне интервала . Если предположить, что канал является случайным, но не изменчивым в течение этого интервала, то k волна может быть выражена комплексным rv . Коррелируя выход канала с результаты ковариации в каждой эпохе j следующие

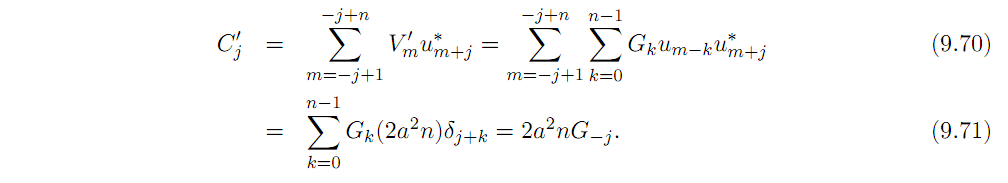
Таким образом, результат корреляции, в отсутствие шума, есть множество фильтрованных волн канала, масштабируемых и обратных во времени/

Это легче понять, глядя на свертывание с :

При этом используется тот факт, что свертывание последовательностей (как свертывание функций) является одновременно ассоциативной и коммутативной. Обратите внимание, что результат свертывания с фильтром согласования является обращенным во времени результатом корреляции, и, таким образом, простой масштабируемой копией волн канала. Наконец отметим, что фильтр согласования равен нулю вне интервала [-n, -1]. Таким образом, если мы представляем реализацию измерения канала с использованием таких дискретных фильтров, мы предполагаем (концептуально), что временные ссылки приемника отстают от временных ссылок передатчика на минимум n эпох.

С добавлением шума, общий выход , то есть выход в эпоху m равен . Таким образом, свертывание выхода шумного канала с фильтром согласования является

После деления на , k-й компонент этого вектора равен

где определена как комплексная случайная переменная

Эта процедура оценки изображена на рисунке 9.9.

Рисунок 9.9: изображает измерение канала с помощью фильтра согласования на PN входе. Мы предполагаем, что G отлична от нуля только в интервале , так что выход наблюдается только в этом интервале. Обратите внимание, что компонент G на выходе является ответом фильтра согласования на вход u, в то время как Ψ является ответом на Z.

Предположим, что шум канала - белый Гаусовский шум, так что переменные шума дискретного времени симметричны по кругу и, где ширина полосы основного потока.

Так как u ортогональна к каждому своему временному сдвигу, то его фильтр согласования вектора должен иметь то же свойство. Отсюда следует, что

Случайные переменные являются совместно гауссовскими из (9.74) и не коррелирует с (9.75), так что они являются независимыми гауссовскими rv’s. Это просто дополнительное упражнение, чтобы показать, что каждый является симметричным по кругу, то есть, .

Возвращаясь к (9.73), можно увидеть, что для каждого , ML оценка от наблюдения определяется

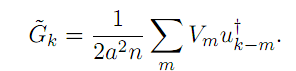
Это также показывает, что эта ML оценка от всего наблюдения V, но вывод этого достаточно сложен. Из (9.73), ошибка в этой оценке - , также означает среднеквадратичную ошибку реальной части этой оценки, а так же в мнимой части, определяемой как

При увеличении длины измерения n или увеличивая входную величину a, мы можем сделать оценку произвольно хорошей. Обратите внимание, что средняя квадратичная ошибка не зависит от затухающих переменных ; шум в оценке не зависит от того, насколько хорош или плох канал. Наконец заметим, что энергия во всем сигнала измерения равна , так что средняя квадратичная ошибка обратно пропорциональна энергии измеряемого сигнала.

В течение, какого времени действительны измерения канала? К счастью, для большинства беспроводных приложений, время согласования во много раз больше, чем задержка распространения. Это делает возможным измерение канала и использование этих измерений для заметного числа символов данных. Существует, конечно, компромисс, так, использование долгого периода измерений n, приведет к точному измерению, но значительная часть будет использована для измерений, а не для данных. Этот компромисс становится менее критичным, так как время согласования увеличивается.

Один эффективный метод, который может быть использован для увеличения количества символов данных входящих в один интервал измерения, заключается в том, чтобы проиводить измерения в середине кадра данных. Это также возможно для данного символа данных, при интерполяции между предыдущем и следующем измерениями канала. Эти методы используются в популярном мобильном стандарте GSM. Данные методы незначительно увеличивают задержки, и на начальных данных в кадре они не могут быть обнаружены до проведения измерения. Однако, если используется кодирование, эта задержка необходима в любом случае. Мы также видели, что одной из основных целей измерения является помощь в управлении мощностью и скоростью на передатчике, и это очевидно, не может быть осуществлено, пока не выполнено измерение.

Данный метод измерения опирается на существование PN последовательности, которая аппроксимирует корреляционные свойства (9.67). PN последовательности (в двоичной форме) порождаются процедурами очень похожими на те, что генерируются на выходных потоках декодера, который осуществляет свертывание. В этом декодере с ограниченной длиной n, каждый бит в данном выходном потоке является суммой по модулю 2 текущего входа и некоторых определенных схем, предыдущих n входов. Здесь нет входов, но вместо этого, выход регистра сдвига подается обратно на вход, как показано на рисунке 9.10.

Рисунок 9.10: Максимальная длина регистра сдвига с n = 4 этапам и длиной цикла , цикл включает все состояния, кроме 0.

При выборе этапов, которые будут суммироваться по модулю 2 соответствующим образом (обозначается максимальная длина регистра сдвига), любое ненулевое начальное состояние будет проходить все возможные ненулевые состояния, пока не вернется в исходное состояние. Известно, что максимальная длина регистров сдвига существуют для всех натуральных чисел n.

Одно из приятных свойств максимальной длины регистра сдвига это линейность (сложение и умножение по модулю 2). То есть, пусть есть у последовательность длиной бит, сгенерированных начальным состоянием х, и пусть есть у’ последовательность, сгенерированная начальным состоянием х’. Тогда можно увидеть, что у ⊕ y’ генерирует x ⊕ x’. Таким образом, разница между любыми двумя такими циклами начинается в разных начальных состояниях содержащих единиц и нулей. Иными словами, множество циклов образует двоичный простой код.

Видно, что любой ненулевой цикл максимальной длины регистра сдвига имеет почти идеальную корреляцию с циклический сдвигом на себя. Однако, эта корреляция происходит в течение одного периода, где последовательность сдвига устанавливается равной нулю за пределами этого периода, что очень важно. Нет гарантии, что такая корреляция близка к идеальной, хотя эти последовательности регистра сдвига обычно используют на практике, приближая её к идеалу.