Волжская государственная академия водного транспорта

(Н. Новгород)

К.Р. Чернышев

Институт проблем управления им. В.А. Трапезникова ран

Россия, 117997, Москва, Профсоюзная ул., 65

E-mail: sicpro@ipu.rssi.ru

Т.И. Гаврилова. Официальное наименование организации соавтора

Страна, ИНДЕКС, Город, Улица, ДОМ

Ключевые слова: идентификация систем, задачи управления, SICPRO ‘08, подготовка статьи, сборник трудов, руководство для авторов

Key words: system identification, control problems, SICPRO ‘08, paper preparation, conference proceedings, author guideline

Для оценки устойчивости судна на курсе проблема несколько усложняется, т.к. практически все подвижные объекты, в том числе и суда, при непереложенных рулях выходят на самопроизвольную циркуляцию с большим или меньшим радиусом, т.е. теоретически являются неустойчивыми на заданном направлении. Для таких объектов вводится понятие эксплуатационной устойчивости. Эксплуатационная устойчивость на курсе считается удовлетворяющей требованиям Правил, если диаметр установившейся циркуляции Dц (при перекладке руля =0) составляет 10 длин судна или более, что на практике выражается в том, что судно удерживается на заданном направлении не более чем 5 – 7 перекладками в минуту.

Известно, что существует зависимость свойств управляемости от соотношений главных размерений судна L/B, T/L и B/T (L – длина, B – ширина, T – осадка) [1]. В то же время, подробных данных о степени влияния того или иного соотношения на управляемость судна, практических рекомендаций о методике выбора параметров L, B, T для достижения наилучшей управляемости в изученной литературе не рассматривается. Поэтому была поставлена задача оценки степени влияния главных размерений судна L, B, T на его управляемость.

Многокритериальный подход в задаче повышения управляемости речных водоизмещающих судов

Для безопасности судоходства Российский Речной Регистр требует от проектировщиков судов соблюдения ряда норм, обеспечивающих остойчивость, ходкость, непотопляемость. C 2004 г. в правила Регистра включены также нормы, предъявляемые к маневренности судов.

Так, в разделе 15 главы 1 Правил классификации и постройки судов внутреннего плавания Российского Речного Регистра^ содержатся требования, предъявляемые к маневренности водоизмещающих самоходных грузовых судов длиной 40 м и более, а также для водоизмещающих пассажирских, разъездных (для перевозки не более 12 пассажиров) и судов специального назначения длиной 20 м и более.

Судно признается отвечающим требованиям в отношении маневренности, если оно удовлетворяет критериям поворотливости, устойчивости на курсе, критерию управляемости при неработающих движителях и некоторым другим.

Рассмотрим два требования, которые представляют интерес не только с точки зрения безопасности судоходства, но и с точки зрения разработки алгоритма автоматического управления движением судна: поворотливость и устойчивость на курсе. Далее в работе под управляемостью будем понимать эти два свойства маневренности – поворотливость и устойчивость, причем при анализе поворотливости будем рассматривать радиусы циркуляции или угловую скорость поворота  при небольших перекладках руля  (рабочий диапазон 5  7), т.к. большие перекладки в режиме авторулевого нежелательны.

Под критерием поворотливости по Правилам Российского Речного Регистра понимают наименьший относительный диаметр установившейся циркуляции Dц _min /L, то есть отношение наименьшего возможного диаметра циркуляции Dц _min , выполняемой судном на глубокой тихой воде при одинаковой до начала маневра и более не регулируемой частоте вращения всех гребных винтов, к длине судна L по конструктивной ватерлинии. Поворотливость считается удовлетворяющей требованиям Правил, если наименьший относительный диаметр установившейся циркуляции отвечает условию Dц _min /L  2.

Для оценки устойчивости судна на курсе проблема несколько усложняется, т.к. практически все подвижные объекты, в том числе и суда, при непереложенных рулях выходят на самопроизвольную циркуляцию с большим или меньшим радиусом, т.е. теоретически являются неустойчивыми на заданном направлении. Для таких объектов вводится понятие эксплуатационной устойчивости. Эксплуатационная устойчивость на курсе считается удовлетворяющей требованиям Правил, если диаметр установившейся циркуляции Dц (при перекладке руля =0) составляет 10 длин судна или более, что на практике выражается в том, что судно удерживается на заданном направлении не более чем 5 – 7 перекладками в минуту.

Известно, что существует зависимость свойств управляемости от соотношений главных размерений судна L/B, T/L и B/T (L – длина, B – ширина, T – осадка) [1]. В то же время, подробных данных о степени влияния того или иного соотношения на управляемость судна, практических рекомендаций о методике выбора параметров L, B, T для достижения наилучшей управляемости в изученной литературе не рассматривается. Поэтому была поставлена задача оценки степени влияния главных размерений судна L, B, T на его управляемость.

Рис. 1. Качественный вид статических характеристик управляемости: А – устойчивые на курсе суда, В, С – неустойчивые.

Анализ характеристик управляемости речных водоизмещающих судов, построенных по результатам натурных экспериментов, позволил сделать вывод о том, что при больших перекладках руля, близких к максимально возможным, суда могут иметь практически одну и ту же, обеспечивающую требование поворотливости Dц _min /L  2, угловую скорость *. Если сравнивать характеристики управляемости при небольших перекладках руля (0 – 10, назовем их _Р) можно заметить, что угловые скорости поворота _Р для различных судов при одинаковых величинах перекладок существенно различаются. Таким образом, по характеру поведения при рабочих перекладках руля суда можно разделить на три типа (рис. 1): А – устойчивые на курсе, но с плохой поворотливостью, В – с плохой эксплуатационной устойчивостью, но хорошей поворотливостью и С – промежуточный вариант между типами А и В. Надо отметить, что все речные водоизмещающие суда являются неустойчивыми на курсе.

Исследование динамических особенностей неустойчивых на курсе судов, как по моделям, так и по осциллограммам натурных испытаний, показал [2, 3], что эти суда обладают рядом нежелательных свойств, а именно: 1) поведение таких судов при управлениях меньше некоторой критической величины _кр. является неоднозначным и только при управлениях больше _кр. полностью предсказуемо; 2) на плоскости статической характеристики такие суда имеют область пониженной управляемости (область С, рис.2), т.е. зону, где имеет место эффект фазового пятна [3]. Этот эффект проявляется в том, что при некоторых сочетаниях координат состояния, когда , снижается чувствительность судна к перекладке руля, т.е. время перехода объекта из состояния с в состояние (рис. 2) существенно увеличивается.

Зарождение фазового пятна происходит при значениях управления  = _кр., а его влияние наблюдается до перекладок руля, превышающих _кр. в 3  5 раз. На практике «попадание в пятно» означает временное ухудшение управляемости судна, что в ряде ситуаций может иметь опасные последствия.

Рис. 2. Возможные статические характеристики управляемости судна, С – области фазовых пятен.

Суда, близкие к устойчивым на заданном направлении (имеющие статическую характеристику типа А), несмотря на способность удерживаться на курсе (при =0, ₀=0) и отсутствие области неоднозначной реакции на управление, имеют плохую поворотливость при _Р (рис. 1, 2), и для достижения величины скорости   _Р требуется значительное увеличение управления.

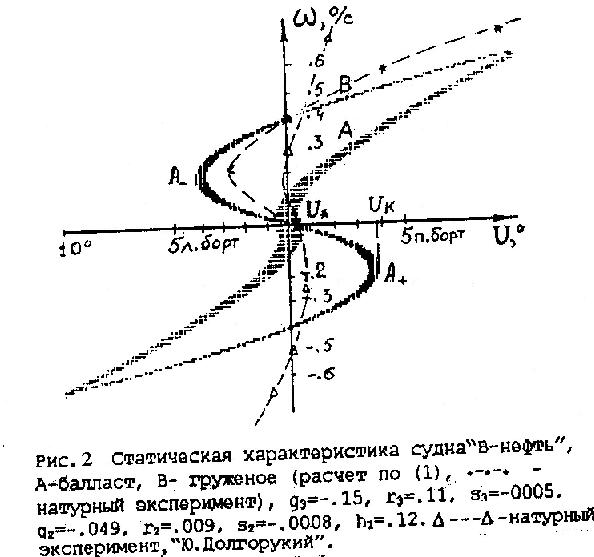
Таким образом, разные конструкции судов отличаются следующими величинами: _кр., ₀, _Р. По данным натурных экспериментов, существуют суда, обладающие одновременно неплохой эксплуатационной устойчивостью (₀ невелико), хорошей управляемостью (угловая скорость _Р достаточно большая) и незначительной величиной _кр (судно «Ю. Долгорукий», рис. 3). В связи с этим была поставлена задача: оценить влияние главных размерений судна L, B и T на указанные величины с целью уменьшения _кр. и ₀ с одновременным увеличением _Р.

За частные критерии оптимальности приняты три вышеуказанные величины:

_кр.(L, B, T), ₀ (L, B, T), _Р (L, B, T).

Требуется найти такие значения параметров L, B, T, которые могли бы одновременно обеспечить min _кр., max ₀, max _Р при ограничениях:

*_кр > _кр > 0, *₀ > ₀ > 0, *_Р > _Р > ₀,

где *_кр, *₀, *_Р – максимально допустимые значения для конкретного проекта судна. Допустимая область изменения L, B и T была определена в диапазоне 10%. Это ограничение связано с требованием не производить перерасчет характеристик движительно-рулевого комплекса.

Для решения поставленной задачи использовалась математическая модель теоретического судна в безразмерных величинах, полученная при условии постоянства скорости хода в условиях глубокой спокойной воды, приведенная в справочнике по теории корабля [1]:

1. 

 – угловая скорость поворота,  – угол дрейфа,  – угол курса, V – скорость движения судна.

Для построения характеристики управляемости (одной из её ветвей) для имеем:

(2)

В моделях (1) и (2) q₃₁, r₃₁, s₃₁, q₂₁, r₂₁, s₂₁, h₁ – коэффициенты модели движения судна, зависящие от параметров, характеризующих корпус судна, его движительно-рулевой комплекс и учитывающие действующие на судно силы и моменты сил.

Для расчета q₃₁, r₃₁, s₃₁, q₂₁, r₂₁, s₂₁, h₁ использовались следующие зависимости [1]:

(3) ,

(4) ,

(5) ,

(6) ,

(7) ,

(8) ,

(9) , где

В этом случае система (2) с учетом формул (3) - (11) принимает вид:

(10)

В связи с тем, что в уравнениях статического режима (12) параметр L не присутствует, при решении оптимизационной задачи варьировались параметры B и T.

Связь между частными критериями _кр , ₀ , _Р и параметрами судна B, T была получена в виде полиномов:

(11) ,

(12) ,

, где

, , – оценки искомых величин, а – нормированные значения главных размерений.

В качестве базовых значений L₀, B₀ и T₀ были взяты соответствующие величины теоретического судна из [1]: L₀ = 100 м, B₀ = 17 м и T₀ = 4,6 м . При этом разброс значений B и T при отклонении их на 10% составили:

B _min = 15.3 м ( = -1) и B_max = 18.7 м ( = +1),

T _min = 4.14 м ( = -1) и T _max = 5.06 м ( = +1).

Для перехода от фактических к нормированным значениям использовались формулы:

(13) ,

Для оценки коэффициентов моделей (13) - (15) с помощью номограмм [1] и формул (3) – (11) были подсчитаны коэффициенты , , , , , , модели (12), которая использовалась для определения опорных значений _кр , _{0 ,} _Р. Результаты расчетов представлены в табл. 1.

Таблица 1.

№ п/п			кр	0	Р
1	0	0	2.5	0.76	1.1	-0.39	0.32	-0.09	70.58	-100.98	-18.45	336.45
2	-1	0	5.5	1.25	1.6	-0.31	0.27	-0.09	4.58	-10.17	-1.84	24.16
3	+1	0	0.6	0.35	0.82	-0.49	0.37	-0.09	10.74	-10.07	-1.84	43.52
4	0	-1	4.1	0.96	1.3	-0.38	0.32	-0.09	5.85	-10.01	-1.84	29.83
5	0	+1	1.7	0.6	1.02	-0.41	0.32	-0.09	8.76	-10.05	-1.84	36.11
6	-1	-1	6.31	1.49	1.72	-0.29	0.27	-0.09	4.18	-9.97	-1.84	18.64
7	+1	-1	1.2	0.49	0.9	-0.46	0.37	-0.09	8.47	-10.04	-1.84	38.83
8	-1	+1	2.9	1.21	1.11	-0.28	0.27	-0.09	4.98	-10.04	-1.84	26.65
9	+1	+1	0.2	0.15	0.68	-0.52	0.37	-0.09	12.42	-10.01	-1.84	45.90

С использованием данных таблицы 1 были построены модели в виде полиномов первого (17, 18, 19) и второго порядков (20, 21, 22):

(14)

(15)

(16)

(17)

(18) .

(19) .

Сравнение результатов значений , , с опорными значениями _кр , _{0 ,} _Р, не участвующими в расчетах, показало, что квадратичные модели дают меньшую погрешность, поэтому для дальнейших вычислений использовалась модель второго порядка.

На рис. 4, 5, 6 показаны зависимости частных критериев от нормированных значений осадки и ширины судна . Анализ построенных зависимостей показывает несовместимость требований, накладываемых на частные критерии.

Таким образом, данная задача была сведена к многокритериальной задаче поиска компромисса [4].

Рис. 4. Зависимость частного критерия a_кр от нормированных величин главных размерений корпуса судна и .

Рис. 5. Зависимость частного критерия ₀ от нормированных величин главных размерений корпуса судна и .

Рис. 6. Зависимость частного критерия _Р от нормированных величин главных размерений корпуса судна и .