Закон Малюса

При пренебрежении ослаблением света за счет потерь на поглощение, отражение и рассеяние, интенсивность света 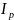, прошедшего поляризатор ,в 2 раза меньше интенсивности естественного света, падающего на него:

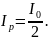
Если разложить каждый из векторов в естественном луче (эти векторы, напомним, имеют всевозможные ориентации) на две компоненты 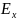и 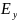, а затем просуммировать соответствующие векторы (рис. 3.4), то ввиду равновероятности ориентаций векторов , суммы компонент всех векторов напряженности будут равны. А значит, будут равны и интенсивности соответствующих компонент. Через поляризатор пройдет только та составляющая вектора , которая параллельна его оси. Следовательно, интенсивность луча, прошедшего через поляризатор, будет равна половине интенсивности падающего на него естественного света.

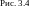
Чтобы убедиться в том, что световой луч при выходе из поляризатора поляризован, и выяснить направление его поляризации, на пути луча ставят анализатор. Если плоскости пропускания анализатора и поляризатора параллельны друг другу, то поляризованный свет пройдет через анализатор без изменения интенсивности (если поглощением света средой можно пренебречь). Если же плоскости поляризатора и анализатора перпендикулярны друг другу, то анализатор полностью погасит падающий на него поляризованный луч. В этом случае говорят, что поляризатор и анализатор скрещены. В промежуточных случаях интенсивность света, прошедшего через анализатор, будет зависеть от взаимной ориентации осей поляризатора. Разберем этот вопрос подробнее.

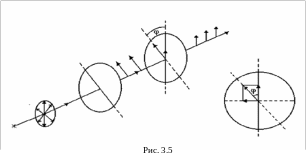
Обозначим амплитуду вектора напряженности электрического поля в луче, прошедшем через поляризатор, как 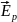(рис. 3.5). Пусть ось поляризатора составляет с осью анализатора угол . Разложим вектор на две составляющие: параллельную плоскости анализатора 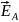и перпендикулярную к ней 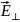. Это соответствует разложению волны, в которой совершаются колебания в плоскости , на две волны, поляризованные во взаимно перпендикулярных плоскостях. Одна из них пройдет через анализатор, а волна с колебаниями светового вектора в перпендикулярной плоскости погасится. Из рис. 3.5 следует, что модуль вектора 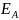при выходе света из анализатора

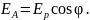
Отношение интенсивностей света пропорционально отношению квадратов амплитуд векторов напряженности электрического поля:

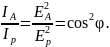
Следовательно,

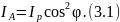
Полученное уравнение выражает закон Малюса: интенсивность света, прошедшего через анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла между осями поляризатора и анализатора.

При скрещенном положении поляризатора и анализатора угол между их осями равен 90^о и свет через анализатор не проходит. Если же оси поляризатора и анализатора параллельны (угол между осями в этом случае равен нулю, а косинус угла – единице), то интенсивность света, прошедшего анализатор, равна интенсивности света, падающего на него.

Если через анализатор пропускать частично поляризованный свет, то интенсивность 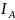прошедшего через него света будет меняться в зависимости от положения оси анализатора, а добиться полного гашения луча никогда не получится. Интенсивность света достигнет максимального значения, если ось анализатора и плоскость преимущественных колебаний частично поляризованного света совпадают. Если же эти плоскости перпендикулярны друг другу, то интенсивность света, прошедшего через анализатор, будет минимальной.