Розрахунки результатів роботи

№ п/п	Назва робіт і витрат	Один. виміру	Вартість одиниці, грн.	Кількість, шт.	Загальна вартість, тис. грн.
1.	Будівництво нульового циклу	м3
2.	Будівництво коробки будівлі	м3
3.	Покрівля і оздоблювальні роботи	м3
4.	Санітарно-технічні роботи	10м
5.	Електромонтажні і низькострумні роботи	100м
6.	Благоустрій території	100м2
	Усього
7.	Накладні витрати (18,1%)
	Усього
8.	Планові нагромадження (10+Nост, %)
	Усього

 Вартість одиниці береться із табл. 5 гр.4.

 Кількість береться із табл. 5 згідно варіанту (гр. 5 – 19 чисельник або знаменник).

Частина№ 3

Тема: Фінансування інвестиційних проектів

Методичні вказівки Найпоширенішою формою фінансування інвестиційних проектів є довгостроковий кредит.

Під час дослідження кредиту найважливішим питанням є вміння знайти величину позикових процентів. Традиційно їх величину визначають за формулою

К_% = К_п · Е_% · Т_п , (24)

де К_% – загальна вартість нарахованих процентів; К_п – сума наданої позики; Е_% – банківський процент (оборотність позикової вартості) за певний час; Т_п – тривалість позики.

Коли до формули (24) застосувати категорійний апарат аналітичної економетрії, то можна одержати

К_% = М_п · Е_% , (25)

де М_п = К_п · Т_п – момент позикової вартості. Геометричний зміст цього показника показано на рис. 5 – це площа, яка знаходиться під графіком зміни величини наданої позики в часі. Формула (25) є найзагальнішою формулою, якою ми будемо користуватись для розрахунку величини нарахованих процентів.

В окремих дослідженнях, коли розраховують вартість довготермінового кредиту, основну увагу звертають не на площу фігур (моменти вартості), що утворюються внаслідок зміни величини заборгованості, а на значення цих заборгованостей. Внаслідок цього для дискретного випадку надання або повернення позики пропонують користуватись такою формулою:

, (26)

де Кзп, Кзк – величина заборгованості на початок і кінець розглянутого планового періоду.

Дійсно, ця формула дає змогу визначати площу ламаної лінії, але не в усіх випадках. Точніший результат можна одержати, застосовуючи формулу:

, (27)

де Т_пі – тривалість і-го планового періоду, протягом якого користуються позикою; М_пі – момент позикової вартості для цього періоду.

Формула (27) має ту перевагу перед попередньою (26), що коли не записувати у явному вигляді значення тривалості планового періоду Т_пі, можна допускати помилки двох видів: перша – не дотримуватись однакових розмірностей, коли розмірність банківського процента Е_% (річний, квартальний чи місячний) не збігається з розмірністю планового періоду Т_пі (рік, квартал, місяць); друга – неправильне визначення моменту вартості (площі), коли початок надання позики або її повернення не збігається з початком і кінцем прийнятого планового періоду, оскільки у такому разі необхідно враховувати тільки ту частину планового періоду, протягом якого фактично користуються позикою. В інших випадках, коли тривалість позики є кратною плановим п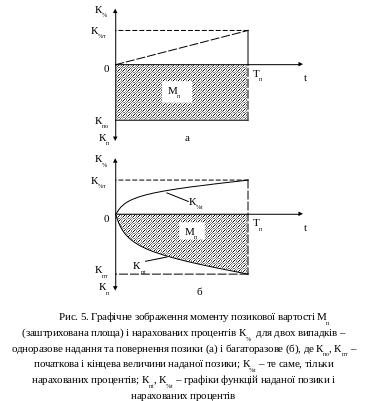 еріодам, показник Т_пі буде дорівнювати одиниці (внаслідок цього і виникає помилкове враження, що цим показником можна нехтувати).

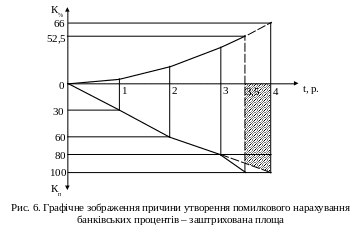
Наприклад, для кредиту 100 тис. грн. (з розподілом за роками 30, 30, 20 і 20 тис. грн.), терміном на 3,5 року під 30% річних, величина нарахованих процентів становитиме відповідно 52,5 і 66 тис. грн. (див. табл. 7 і рис. 6), а різниця між істинною і помилковою сумами нарахованих процентів 13,5 тис. грн. (66 – 52,5).

Таблиця 7

Розрахунок довгострокового кредиту за двома методами

Роки	Розмір взятої позики, тис.грн.	Нараховані проценти (наростаючим підсумком), тис.грн.
		за формулою (4)	за формулою (3)
1	30	4,5	4,5
2	60	18	18
3	80	39	39
3,5 (4)	100	52,5	66

Недоліком формули (26) є і те, що нею незручно користуватись, коли тривалість планового періоду зменшується (прямує до нуля), тобто, якщо надання або повернення позики відбуваються практично як неперервні виплати (щотижня, щодекадно). У такому разі зручніше (і правильніше) користуватись економетричними методами розрахунку кредиту.

На рис. 7 показано, як можна перейти від дискретного методу повернення позики до неперервного, коли оплата здійснюється в кінці планового періоду. Дискретне нарахування процентів виконується за формулою (27) (рис. 7, а).

Якщо періодичність повернення позики збільшити в багато разів (здійснювати щотижня або декадно), тобто коли цей процес набере вигляд рівномірного грошового потоку П_пп, то зміна величини цієї вартості матиме такий вигляд (лінія 1, рис. 7 б)

К_ппt = – К_опн + П_пп·t .

А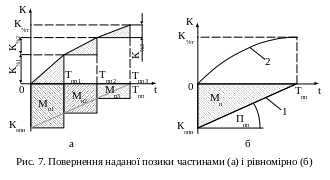 якщо його інтегрувати, можна знайти зміну моменту позикової вартості в часі

,

оскільки П_пп = К_опн/Т_пп = К_опн·Е_пп , де К_опн – загальна величина наданої позики; Т_пп – період повернення позики; Е_пп – оборотність повернення позики.

Використовуючи формулу моментів позикової вартості, одержимо аналітичний вираз для визначення величини нарахованих процентів (лінія 2) за методикою простих процентів, якщо кредит погашається рівномірно

, (28)

Останнім часом для розрахунку довготермінового кредиту застосовують методику ануїтету в поєднанні з дисконтуванням вартості, тобто методику нарахування складних процентів

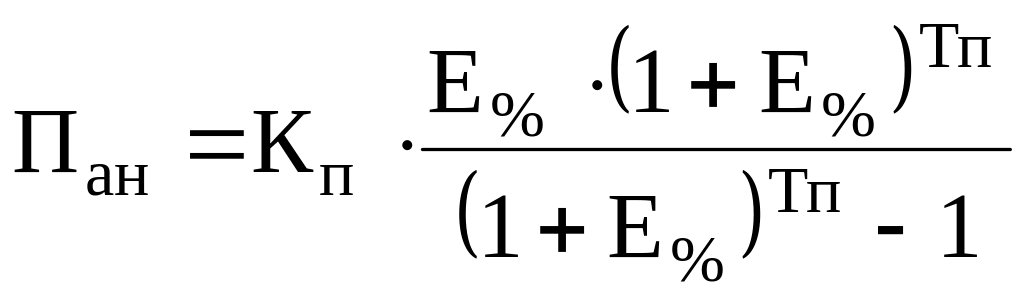, (29)

де П_ан – значення ануїтету (величина періодичних виплат для повернення позики); інші показники попередні.

Позитивним в цій методиці є те, що вона дає змогу порівняно просто і об’єктивно розрахувати, як необхідно повертати позику. Проте ця методика має також окремі недоліки. Певні незручності спричиняє те, що розраховане постійне значення ануїтету П_ан складається із двох частин – нарахованих процентів і величини повернення початкового боргу, тому для визначення їх окремих значень необхідно виконувати додатковий розрахунок.

Для обґрунтування вищесказаного розглянемо такий приклад. Припустимо, що банком був наданий кредит сумою 100 тис. грн. під 30% річних. Клієнт банку зобов’язався повернути кредит протягом 3,5 року. Проаналізуємо три методи повернення кредиту.

Метод 1. Клієнт повертає банку кредит дискретними виплатами. Повернення боргу відбувається такими виплатами (тис. грн.): перший рік 40, другий – 30, третій – 20 і четвертий 10.

Кредит розраховано за формулою (27), результати зведено в таблицю 8, а основні залежності показано на рис. 8.

Таблиця 8

Розрахунок кредиту при дискретних виплатах, тис. грн.

Роки	1	2	3	4
Заборгованість на початок року	100	60	30	10
Нараховані проценти за рік	24	13,5	6	0,75
Сумарні нараховані проценти	24	37,5	43,5	44,25

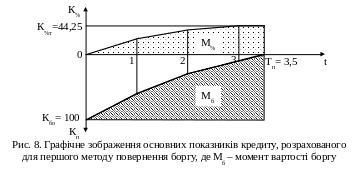
Метод 2. Клієнт повертає банку кредит неперервними виплатами (щотижня). Погашення боргу відбувається рівномірно.

У такому разі розрахунок виконується за формулою (28). Результати розрахунку зведено в табл. 9, а основні залежності показано на рис. 9.

Таблиця 9

Розрахунок кредиту при неперервних (щотижневих) виплатах, тис.грн.

Роки	1	2	3	3,5
Заборгованість на початок року	100	71,43	42,86	14,28
Нараховані проценти за рік	25,71	17,14	8,58	1,07
Сумарні нараховані проценти	25,71	42,85	51,43	52,5

М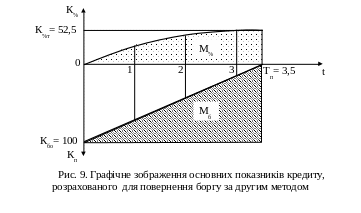 етод 3. Повернення кредиту за методикою ануїтету – формула (29).

Розрахунок за цим методом зведено в табл. 10, а графічне зображення основних показників кредиту для цього випадку повернення кредиту показано на рис. 10.

Недоліком цієї методики є те, що у такому разі також потрібно розраховувати кратну кількість планових періодів. Оскільки тривалість позики становить 3,5 року, то, прийнявши, що сплата буде відбуватись через півроку, таких періодів буде 7. Окрім того, щоб дотримуватись правила розмірностей, необхідно перейти до піврічної величини банківського процента. Тобто вона дорівнюватиме Е_% = 15%. Тоді ануїтет становитиме

тис. грн.

Таблиця 10

Розрахунок повернення позики за методом 3, тис. грн.

Півріччя	Залишок позики на початок року	15% піврічних	Залишок загальної суми заборгованості на кінець року	Річна плата (ануїтет)	Річна плата тільки за позику
1	100	15	115	24,036	9,036
2	90,964	13,644	104,609	24,036	10,391
3	80,572	12,086	92,658	24,036	11,95
4	68,622	10,293	78,916	24,036	13,743
5	54,88	8,232	63,112	24,036	15,804
6	39,076	5,861	44,937	24,036	18,175
7	20,901	3,135	24,036	24,036	20,901
Разом		68,252		168,252	100

В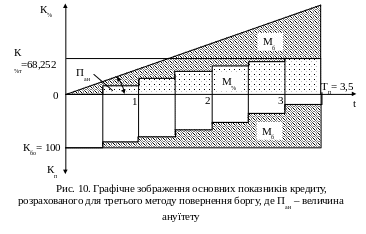 ихідні дані для розрахунку:

1. Величина позики – сума БМР з розрахункової роботи №1.

2. Термін позики Т_п = 4,5 + 0,1ּ№_ост , роки.

3. Банківський кредит Е_% = 5 + 0,1ּ№_ост , % квартальних.

4. Розрахувати повернення кредиту за трьома методами.

Рекомендована література

1. Скворцов І.Б. Аналітичні методи економетрії у сфері інвестицій: Введення в аналітичну економіку. – Львів: Видавництво Державного університету "Львівська політехніка", 1999. – 200 с.

2. Скворцов І.Б. Ефективність інвестиційного процесу (методологія, методи і практика): Монографія – Львів: Видавництво Національного університету “Львівська політехніка”, 2003. – 391 с.

3. Гойко А.Ф. Методи оцінки ефективності інвестицій та пріоритетні напрями їх реалізації. – К.: ВІРА-Р, 1999. – 320 с.

4. Пересада А. А. Управління інвестиційним процесом: Монографія. – К.: Лібра, 2002. – 472 с.

5. Бланк И.А. Инвестиционный менеджмент. – К.: МП "ИТЕМ" ЛТД, "Юнайтед Лондон Трейд Лимитед", 1995. – 448 с.