
- •00Министерство образования и науки украины
- •1.1. Расчет оптимального маршрута задачи коммивояжера методом ветвей и границ
- •1.2. Разработка и расчет параметров схем движения пассажирских судов
- •3.1 Пассажиропоток
- •Расчет показателей
- •3.2.Расчет эксплуатационных показателей работы судов на перевозках пассажиров по выбранной схеме
- •3.3. Расчет экономических показателей
- •Расчет:
- •3.4 Средневзвешенная тарифная ставка
- •3.5 Расчет площадей палуб жилого блока
- •3.6 Определение коэффициента комфортабельности
00Министерство образования и науки украины
ОДЕССКИЙ НАЦИОНАЛЬНЫЙ МОРСКОЙ УНИВЕРСИТЕТ
КАФЕДРА МОРСКИХ ПЕРЕВОЗОК
ПРАКТИЧЕСКИЕ РАБОТЫ
К МОДУЛЮ №1
ПО ДИСЦИПЛИНЕ
«МОРСКИЕ ПАССАЖИРСКИЕ ПЕРЕВОЗКИ»
На тему:
«МАРКЕТИНГОВЫЙ АНАЛИЗ КРУИЗНОГО РЫНКА»
МОДУЛЬ 1
Выполнил:
Студент 3к., 1гр. ФТТиС
Бондаревский М.В.
Проверила:
Сильванская Г.Н.
ОДЕССА-2011
1.1. Расчет оптимального маршрута задачи коммивояжера методом ветвей и границ
Имеется 5 портов, расстояния между которыми заданы в таблице 1 в виде C=cij, i,j=(1…n). В таблице 1 каждому порту назначен номер от 1 до 5.
Таблица 1. Расстояния между портами
Порты отхода |
Порты захода |
||||
Одесса(1) |
Констанца(2) |
Сочи(3) |
Стамбул(4) |
Пиреи(5) |
|
Одесса(1) |
∞ |
179 |
448 |
347 |
702 |
Констанца(2) |
179 |
∞ |
483 |
201 |
557 |
Сочи(3) |
448 |
483 |
∞ |
513 |
868 |
Стамбул(4) |
347 |
201 |
513 |
∞ |
360 |
Пиреи(5) |
702 |
557 |
868 |
360 |
∞ |
Учитывая,
что каждое значение cij
является
расстоянием между портом отхода i
и портом захода j,
их величины не могут иметь отрицательного
значения, поэтому cij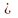 0.
0.
Учитывая особенности работы морского транспорта и географическое расположение портов круиза, наша задача имеет симметричный характер, то есть cij=cij.
Нужно найти кратчайший замкнутый маршрут, который проходит через каждый порт один раз с возвращением в первый базовый порт и который минимизирует суммарное пройденное расстояние. Математическая постановка задания может быть представлена в следующем виде:
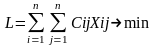 ;
(1)
;
(1)
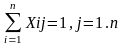 (2)
(2)
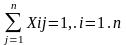 (3)
(3)
Xij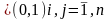 (4)
(4)
Матрица С называется приведенной, когда все ее элементы неотрицательные, а каждый рядок и столбец имеет хотя бы один ноль. Привидение матрицы может быть осуществлено следующим образом:
Шаг 1: Привидение по строкам. По каждой строке i найдем наименьший элемент min cij=ai. Тогда при переходе к приведенной матрице с’=cij – ai. Данные заносим в таблицу 2.
Таблица 2. Матрица, приведенная по строкам
|
1 |
2 |
3 |
4 |
5 |
ai |
1 |
∞ |
179 |
448 |
347 |
702 |
179 |
2 |
179 |
∞ |
483 |
201 |
557 |
179 |
3 |
448 |
483 |
∞ |
513 |
868 |
448 |
4 |
347 |
201 |
513 |
∞ |
360 |
201 |
5 |
702 |
557 |
868 |
360 |
∞ |
360 |
Шаг 2: Привидение по столбцам. В каждом столбце j, который не имеет нулевых элементов, находим наименьшее значение cij=bj, которое отображено в заключительной строке bj приведенной матрицы. Тогда c’’ij=c’ij – bj . Данные заносим в таблицу 3.
Таблица 3. Матрица, приведенная по рядам
|
1 |
2 |
3 |
4 |
5 |
1 |
∞ |
0 |
269 |
168 |
523 |
2 |
0 |
∞ |
304 |
22 |
378 |
3 |
0 |
35 |
∞ |
65 |
420 |
4 |
146 |
0 |
312 |
∞ |
159 |
5 |
342 |
197 |
508 |
0 |
∞ |
bj |
- |
- |
269 |
- |
159 |
Далее составляем приведенную матрицу. Данные заносим в таблицу 4.
Таблица 4. Приведенная матрица G0
|
1 |
2 |
3 |
4 |
5 |
ai |
1 |
∞ |
0-0 |
0-35 |
168 |
364 |
179 |
2 |
0-22 |
∞ |
35 |
22 |
219 |
179 |
3 |
0-35 |
35 |
∞ |
65 |
261 |
448 |
4 |
146 |
0-0 |
43 |
∞ |
0-219 |
201 |
5 |
342 |
197 |
239 |
0-219 |
∞ |
360 |
bj |
|
|
269 |
|
159 |
|
В соответствии с теоремой Эйлера, которая утверждает, что когда мы отсчитываем любую константу из всех элементов строки или столбца матрицы, мы оставляем минимальный тур минимальным.
На пересечении итоговой строки i и столбца j находится величина, которая называется – «сумма приводящих констант», которая равна:
S = 179 + 179 + 448 + 201 + 360 + 269 + 159 = 1795 миль.
Между величинами L и L’ существует следующее соотношение:
L = L’ + S
Таким образом, L≥S, что определяет S как нижнюю границу целевой функции задачи коммивояжера.
Находим степени каждого из нулей приведенной матрицы.
Клетка с max степенью нуля определит дугу, в соответствии с которой будет выполняться последующее ветвление.
Максимальная степень нуля равна 219 и соответствует клеткам (4-5) и (5-4). Выбираем клетку (4-5). Таким образом эта дуга является претендентом на включение в гамильтонов контур.
Разбиваем множество всех гамильтоновых контуров на два подмножества: G1 и G2.
Матрица G1 (исключение дуги 4,5)
|
1 |
2 |
3 |
4 |
5 |
1 |
∞ |
0 |
0 |
168 |
364 |
2 |
0 |
∞ |
35 |
22 |
219 |
3 |
0 |
35 |
∞ |
65 |
261 |
4 |
146 |
0 |
43 |
∞ |
∞ |
5 |
342 |
197 |
239 |
0 |
∞ |
Матрица G2 (включение дуги 4,5)
|
1 |
2 |
3 |
4 |
1 |
∞ |
0 |
0 |
168 |
2 |
0 |
∞ |
35 |
22 |
3 |
0 |
35 |
∞ |
65 |
5 |
342 |
197 |
239 |
∞ |
Приведенная матрица G1 (4,5)
|
1 |
2 |
3 |
4 |
5 |
ai |
1 |
∞ |
0 |
0 |
168 |
145 |
0 |
2 |
0 |
∞ |
35 |
22 |
0 |
0 |
3 |
0 |
35 |
∞ |
65 |
42 |
0 |
4 |
146 |
0 |
43 |
∞ |
∞ |
0 |
5 |
342 |
197 |
239 |
0 |
∞ |
0 |
bj |
0 |
0 |
0 |
0 |
219 |
|
S = 1795 + 219 = 2014 мили
Приведенная матрица G2 (4,5)
|
1 |
2 |
3 |
4 |
ai |
1 |
∞ |
0-0 |
0-35 |
146 |
0 |
2 |
0-0 |
∞ |
35 |
0-43 |
0 |
3 |
0-35 |
35 |
∞ |
43 |
0 |
5 |
145 |
0-42 |
42 |
∞ |
197 |
bj |
0 |
0 |
0 |
22 |
|
S = 1795 + 197 + 22 = 2014 мили
Для дальнейшего ветвления выбираем любую из приведенных таблиц G1 или G2, так как расстояния равны. Выбираем матрицу G2. Блокируем клетки (5-2), чтобы не образовался цикл.
Матрица G2.1 (2,4)
|
1 |
2 |
3 |
1 |
∞ |
0 |
0 |
3 |
0 |
35 |
∞ |
5 |
145 |
∞ |
42 |
Матрица G2.2 (2,4)
|
1 |
2 |
3 |
4 |
1 |
∞ |
0 |
0 |
146 |
2 |
0 |
∞ |
35 |
∞ |
3 |
0 |
35 |
∞ |
43 |
5 |
145 |
∞ |
42 |
∞ |
Приведенная матрица G2.1 (2,4)
|
1 |
2 |
3 |
ai |
1 |
∞ |
0-35 |
0-0 |
0 |
3 |
0-138 |
35 |
∞ |
0 |
5 |
103 |
∞ |
0-103 |
42 |
bj |
0 |
0 |
0 |
|
S = 2014 + 42 = 2056 мили
Приведенная матрица G2.2 (2,4)
|
1 |
2 |
3 |
4 |
ai |
1 |
∞ |
0-0 |
0-35 |
103 |
0 |
2 |
0-35 |
∞ |
35 |
∞ |
0 |
3 |
0-0 |
35 |
∞ |
0-103 |
0 |
5 |
103 |
∞ |
0 |
∞ |
42 |
bj |
0 |
0 |
0 |
43 |
|
S = 2014 + 43 + 42 = 2099 миль
Для дальнейшего ветвления выбираем матрицу G2.1 , так как она имеет наименьшее расстояние.
Матрица G3.1 (3,1)
|
2 |
3 |
1 |
0 |
∞ |
5 |
∞ |
0 |
S = 2056 + 0 = 2056 миль
Таким образом получили гамильтонов цикл 1-2-4-5-6-1.
Круизная линия:
Одесса – Констанца – Стамбул – Пиреи – Сочи – Одесса
Протяженность линии составляет:
S = 179 + 201 + 360 + 868 + 448 = 2056 мили

Рис 1. Ветвление матрицы
