
- •Частные производные функции n-переменных.
- •Производная по направлению и градиент функции n-переменных
- •Поверхность уровня функции n-переменных.
- •Дифференцирование сложных функций.
- •Формула Тейлора
- •Экстремум функции n-переменных
- •Задача Условного Экстремума
- •Понятие о задаче оптимизации.
- •Дифференциальные уравнения.
- •1.1Основные понятия.
- •Дифференциальные уравнения первого порядка.
- •Некоторые сведения об особых решениях.
- •Уравнения второго порядка, допуск понижения.
- •Линейные уравнения первого порядка.
- •Линейные однородные дифференциальные уравнения n-ого порядка с постоянным коэффициентом.
- •Линейные неоднородные дифференциальные уравнения n-ого порядка.
- •Системы дифференциальных уравнений – несколько уравнений взятых вместе.
- •Линейные однородные системы
- •Устойчивость линейной системы. Точки покоя.
- •Кратные интегралы
- •Замена переменной в двойном интеграле
- •Поверхностные интегралы.
Дифференцирование сложных функций.
Сложная функция n-переменных.
 Em
Em
En R
 M=
M=![]() M
z(f)
M
z(f)
T
z=f(![]()
Аналитически:
z=f(х1, х2,…, хn)
х 1=
х1
(t1,
t2,…,
tm)
1=
х1
(t1,
t2,…,
tm)
х2= х2 (t1, t2,…, tm)
:
хn= хn (t1, t2,…, tm)
При дифференцировании сложной функции применяется одна основная формула:
z’tj=![]() z’хi
* xi’tj
j=1…m
z’хi
* xi’tj
j=1…m
Пример:
z=x1 x22+x33 x2
x1=t1 -2 t2
x2= t12 +5 t2
x3= t1 + t23
z’t1=z’x1*x1’t1+z’x2*x2’t1+z’ x3*x3’t1= x22*1+(2*x1 x2+x33)*2t1+3x32 x2 *1
z’t2=x22 (-2)+(x1 2x2+x33)5+3x32x23t22
dz= z’x1 dx1+ z’x2 dx2+ z’x3 dx3
dx1= x1’t1 dt1+ x1’t2 dt2
dx2= x2’t1 dt1+ x2’t2 dt2
dx3= x3’t1 dt1+ x3’t2 dt2
Частные случаи:
1)z= f(х1, х2,…, хn)
х1= х1(t)
х2= х2(t)
х 3=
х3(t)
3=
х3(t)
En
z
t M
z’t= z’xi x’it
2) z= f(х1, х2,…, хn)
х1= х1
х2= х1(х1)
хn= хn(х1)
z’x1=![]() +
+![]() z’xi
xi’x1
z’xi
xi’x1
§8
Неявные функции
Неявной функцией называется задание функциональной зависимости посредством функционального соотношения, не разрешённого относительно какой-либо переменной.
F(z,x1,x2,…,xn)=0
Без дополнительного исследования нельзя сделать никаких выводов о:
Разрешимости соотношения относительно, например z.
Непрерывности получившейся функции.
Дифференцируемости получившейся функции.
Замечание:
Д аже
если нашёлся такой набор чисел
(z0,x10,x20),
что F(z0,x10,…,xn0)
аже
если нашёлся такой набор чисел
(z0,x10,x20),
что F(z0,x10,…,xn0)![]() 0-три поставленных вопроса всё равно
остаются нерешёнными.
0-три поставленных вопроса всё равно
остаются нерешёнными.
Теорема о неявной функции:
П усть
дано функциональное соотношение F(z,x1,
x2,…,xn)
усть
дано функциональное соотношение F(z,x1,
x2,…,xn)![]() ,
пусть N0(z0,
x0,x10,…,xn0)
такая точка n+1
мерного пространства, что F(N0)
0
,
пусть N0(z0,
x0,x10,…,xn0)
такая точка n+1
мерного пространства, что F(N0)
0
Пусть
F
как функция n+1 переменной дифференцируема
в точке N0,
и при этом F’z
![]() 0,тогда
существует такая окрестность М0
(x10,x20,…,xn0)
Еn в
которой z
является однозначной
N0
0,тогда
существует такая окрестность М0
(x10,x20,…,xn0)
Еn в
которой z
является однозначной
N0
непрерывной, дифференцируемой функцией оставшихся n-переменных z=f(x1, x2,…,xn) и при этом выполняется следующее соотношение:
![]() i=1,n
i=1,n
Геометрически данная теорема означает следующий факт:

z


 F(z,x1,
x2,…,xn)=0
(поверхность)
F(z,x1,
x2,…,xn)=0
(поверхность)





 N0
N0
 «График»
функции z=f(x1,
x2,…,xn)
«График»
функции z=f(x1,
x2,…,xn)
М0
х1
х2 хn
х3
З амечание:
амечание:
Если
производная ![]() =
0, то кусочек поверхности может неоднозначно
спроектироваться в окрестность точки
М0.
=
0, то кусочек поверхности может неоднозначно
спроектироваться в окрестность точки
М0.
N0
Пример:
z2+x12+x22-R2=0 R=const
F(z,x1, x2)
Выяснить:
задает ли оно z
как функцию x1,
x2,
если да –
найти ![]()
F’z=2z
Она
равна 0
![]() => все точки вида N(x1,
x2,0)-
надо исключить т.к. не выполняется
условие теоремы.
=> все точки вида N(x1,
x2,0)-
надо исключить т.к. не выполняется
условие теоремы.

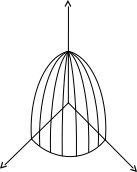



 R график
z
как z=f(x1,
x2)
R график
z
как z=f(x1,
x2)
N0


 R
R
N1
R
R
N1
 N1
N1
Положение верхней и
Плохой график нижней части

F’x1=
-
![]()
F’x2=
-
![]()
Касательная плоскость
П усть
функция z=f(М)
дифференцируема в точке М0
тогда к
графику этой функции в точке N0
(М0;z0)можно
провести касательную плоскость с
уравнением:
усть
функция z=f(М)
дифференцируема в точке М0
тогда к
графику этой функции в точке N0
(М0;z0)можно
провести касательную плоскость с
уравнением:
z - z0= z’xi (xi- xi0) причём плоскость единственная.
M0

Модификация:
Пусть функция z=f(М) задана неявно соотношение F(z,x1, x2,…,xn) в окрестности точки M0, причем выполняются все условия теоремы о неявной функции, тогда к поверхности F(z,x1, x2,…,xn) в точке N0 можно провести единственную касательную плоскость с уравнением:
 F’xi
(xi-
xi0)+
F’z
(z-z0)=0
F’xi
(xi-
xi0)+
F’z
(z-z0)=0
N0 N0
Пример 1:
z=x12+x22, М0(2;3) => z0=13 =>N0(2;3;13)
z’x1=2 x1=4
z’x2=2 x2=6
z-13=4(x1-2)+6(x2-3)
z=4x1+6x2-13
П ример
2:
ример
2:
z2-x12-x22=0
F(x1, x2, z)
М0(1;3)
=>N0(1;3;![]() ),
F(N0)
),
F(N0)![]() 0
0
F
’z=2z=>
F’z
2![]() 0=>
теорема о неявной функции верна.
0=>
теорема о неявной функции верна.
N0
F’x1= -2 x1= -2
F’x2= -2 x2= -6
Касательная плоскость
-2(x1-1)+(-6(x2-3))+2 +(z- )=0
-2x1-6x2+2 +20-20=0
Определение:
Нормалью к поверхности называется вектор перпендикулярный касательной плоскости.
Н ормали
две: одна внешняя другая внутренняя.
ормали
две: одна внешняя другая внутренняя.









![]()
![]()
Чаще всего в приложениях используются единичная нормаль, такая длина которой равна 1.
Координаты единичной нормали:
1)Поверхность в явной форме:
![]() =
=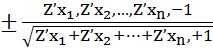
При переходе от точки к точке координаты нормали, вообще говоря, меняются.
2)Поверхность в неявной форме
=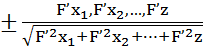
Замечание:
П ри
рассмотрении поверхности в неявной
форме возможна ситуация, когда в точке
N0
все производные
равны 0:
ри
рассмотрении поверхности в неявной
форме возможна ситуация, когда в точке
N0
все производные
равны 0:
![]() =
=![]() … =
… =![]() =0
=0
N0 N0 N0
Такая точка N0 называется особой точкой поверхности; в этой точке касательная плоскость и нормаль неопределены, а структура поверхности в окрестности этой точки может быть достаточно сложной – поверхность нельзя однозначно спроецировать ни на одну координатную плоскости.
Пример:
z2-x12-x22=0
N0(0;0;0)
F(N0) 0
![]() =2z
=2z
![]() =
-2 x1
=
-2 x1
![]() =
-2 x2
=
-2 x2
В точке N0 все эти производные равны 0 => N0 особая точка поверхности
x12+x22= z2 – круговой конус
 z
z









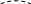
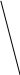
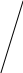

 U(0)
U(0)
0
x1 x2
Однозначно спроецировать куски конуса в окрестности точки 0 на координатные плоскости невозможно -произойдёт наложение.
Производные и дифференциалы высших порядков.
Отметим:
Поскольку частные производные сами по себе являются функциями тех же n-переменных, то они могут быть дифференцированными и от них тоже можно брать свои частные производные.
При этом возможны два случая:
1)Каждый раз дифференцирование ведётся по одной и той же переменной, такие производные называются «чистыми» и обозначаются:
![]() или
или ![]()
2)Переменная, по которой ведётся дифференцирование, от раза к разу меняет наименование; такие производные называются смешанные и обозначаются следующим образом.
![]() k+m+…+p=n
k+m+…+p=n
или
![]()
Теорема Шварца:
Если смешанные производные непрерывны а точке М0, то их значение не зависит от порядка дифференцирования.
![]() =
= ![]()
z=x14 x22 +x35 x23 –x12
z’x1=4 x13 x22- 2x1
z’x2=2 x2 x14+3x22 x35
z’x3=5 x34 x23
z’’x12=12 x12 x22- 2
z’’x1 x2=8 x13 x2
z’’x2x1 =8 x2 x13
z’’’ x1 x22=8 x13
z’’’ x12 x2= (z’’x1 x2) x1=24 x12 x2
Аналогично функции одной переменной для функций n-переменных можно ввести дифференцирование высших порядков.
![]()
:
![]()
![]() =d
f
’xi
dxi=
d(
f
’xi
dxi)=
dxi*d
f
’xi
=
dxi(
=d
f
’xi
dxi=
d(
f
’xi
dxi)=
dxi*d
f
’xi
=
dxi(![]() f
’’xi
xj
dxj)=
f
’’xi
xj
dxj)=
=
![]() f ’’xi
xj
dxi
dxj=d2
f(M)
f ’’xi
xj
dxi
dxj=d2
f(M)
Замечание:
Если второй дифференциал считается в конкретной точке М0 ,то все частные производные становятся числами, а сам второй дифференциал превращается в квадратичную форму относительно приращений независимых переменных.
Пример:
z=x13+x12 x24 x23 +x33 М0(1;2;1)
d 2z - ?
М0
d
2z
=
![]() z’’xi
xj
dxi
dxj=
z’’x12
(dx1
)2+
2z’’x1
x2
dx1
dx2+
2z’’x1
x3
dx1
dx3+
z’’x22
(dx2
)2+
z’’xi
xj
dxi
dxj=
z’’x12
(dx1
)2+
2z’’x1
x2
dx1
dx2+
2z’’x1
x3
dx1
dx3+
z’’x22
(dx2
)2+
М0 М0 М0 М0 М0 М0
+ 2z’’x2
x3
dx2
dx3+
z’’x32
(dx3
)2
=
2z’’x2
x3
dx2
dx3+
z’’x32
(dx3
)2
=
М0 М0
z’x1=3 x12+2 x1x24
z’x2=4x12 x23
z’x3=3 x32
z’’x12=6 x1+ 2x24=38
z’’x22=12 x12 x22=48
z’’x32=6x3=6
z’’x1 x2=8 x1 x23=64
z’’x1x3 =0
z’’x2x3 =0
= 38(dx1 )2+128 dx1 dx2+0 dx1 dx3+48(dx2 )2+0 dx2 dx3+6(dx3 )2
В полученном выражении приращение независимых переменных входят как аргументы, причём в каждое слагаемое суммарно во второй степени, (квадратная форма)
Аналогично, можно получить формулы для дифференциалов любого порядка:
![]() =
=![]() f
kxi
xjxk
dxi
dxj
dxk
f
kxi
xjxk
dxi
dxj
dxk
Для простоты при вычислении дифференциала k-ого порядка используется «биномиальная форма».
![]() =(
=(![]() k
f
(k-понимается
как степень)
k
f
(k-понимается
как степень)
Пример:
Найти дифференциал третьего порядка, если z=f(x1 x2 ) является функцией двух переменных.
![]() =(
=(![]() 3
3
![]() = ((
= (( ![]() )3+3(
)2
)3+3(
)2![]() +3
(
)2+(
)3)f
=
+3
(
)2+(
)3)f
=
=
( ![]() +3
+3![]() +3
+3![]() +
+![]() )f=
)f=
=(
![]() +3
+3![]() +3
+3![]() +
+![]()
§9
