Пример:

Общее решение уравнения будет: ; особое решение : 0=x + 2C

Проверим, что последняя функция действительно является решением исходного уравнения:

Дифференциальное уравнение n-ного порядка

Общее решение в неявном виде (должно содержать n произвольных независимых постоянных):

Либо общее решение может быть найдено в явном виде:

Пример:

Если задать начальные условия: y (0) = y₀ , V(0)=V₀ , то V₀=С₁ y₀=С₂

Чтобы решить задачу Коши для дифференциального уравнения 1-го порядка: , т.е. найти функцию-решение (интегральную кривую), проходящую через данную точку, достаточно задать 1 условие: y(х₀)= y₀.

Теорема: Пусть функция определена и непрерывна в области . Пусть непрерывны в . Тогда задача Коши, состоящая в нахождении решения уравнения с начальными условиями (где точки принадлежат области ) имеет, притом единственное решение y = y(x), в окрестности x=x₀. (без доказательства).

Линейные дифференциальные уравнения

Линейным дифференциальным уравнением называется уравнение вида:

(1)

При q=0, уравнение называется однородным, q0 неоднородным.

y+py=q –дифференциальное уравнение первого порядка.

Обозначим левую часть уравнения (1) при q(x)=0 L(y)=>L(y)=0.

Отметим два свойства L(y).

1. L(y₁+y₂)=L(y₁)+L(y₂)

2. L(Cy)=CL(y) => множество решений линейно однородного дифференциального L(y) = 0 есть линейное пространство.

Линейная зависимость функций

Функции y₁,…,y_n называются линейно зависимыми, если  λ₁,…,λ_n (|λ₁|+…+|λ_n|0) такие что соответственно функции называются линейно независимыми если не удовлетворяют уравнению (1) при любом .

Множество решений n-мерного дифференциального уравнения образуют базис, состоящий из линейно независимых функций.

Определитель Вронского.

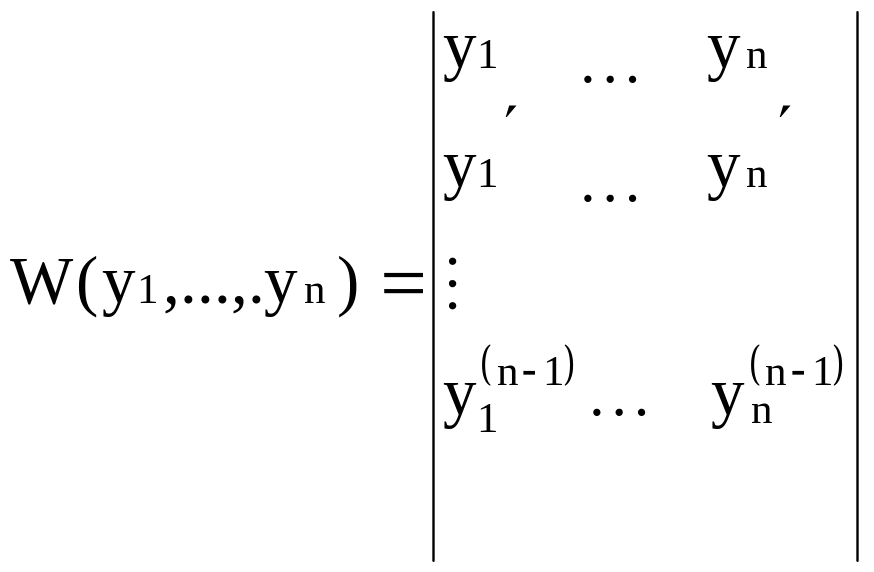
Теорема 1:

Если функции y₁(x),…,y_n(x)(все функции и их производные непрерывны и существуют до n-1 го порядка) линейно зависимы, то =0.

Доказательство:

Так как функции линейно зависимы, то после дифференциирования получим:

, Эта система имеет ненулевое решение  когда определитель этой системы равен 0. А этот определитель и есть определитель Вронского.

Если W0, то функции линейно независимы.

Пример 1:

Покажем, что если определитель равен нулю, то функции необязательно линейно зависимы. ,

Рассмотрим произвольную точку x₀>0.

Теорема 2: Пусть решения уравнения и тогда

Следствие: если хотя бы в одной точке (a,b) тогда  x (a,b) W(x)0 и функции линейно независимы.

Доказательство:

Так как W=0 в x₀, то так как определитель =0 то его столбцы линейно зависимы (их линейная комбинация равна 0). Значит

Рассмотрим функцию y= L(y)=0, т.е. y- решение дифференциального уравнения. С условиями:

Решение удовлетворяет (1) но начальным условиям удовлетворяет только одно решение (по теореме Коши о существовании единственного решения). y(x)  0 и – линейно зависимы => W = 0.

Пример 1:

y⁽ⁿ⁾=0 Решения:y₁=1, y₂=x, y₃=x²,…,y_n=x^n-1

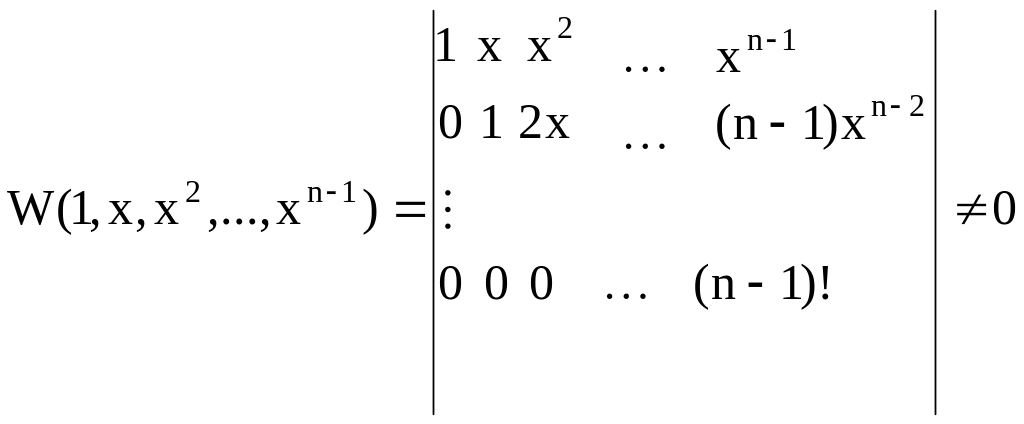
следовательно, функции линейно независимы.

Пример 2:

Значит функции sinx и cosx линейно независимы.

Пример 3:

,