Знакопеременные ряды

Пусть и ряд сходятся одновременно, то А также и при этом говорят, что ряд A сходится абсолютно.

Если сходится, – расходится, то А сходится условно.

Признак Лейбница.

(монотонно стремится к 0), тогда A сходится.

Доказательство:

Т.к.

.

, , то есть последовательность частичных сумм A_2n убывает, а A_2n+1 возрастет.

Каждая из последовательностей A_2n и A_2n+1 ограничена и

Следовательно, .

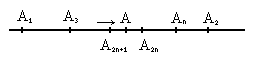
Заметим, что:

.

Пример:

Ряд Лейбница: сходится условно (неабсолютно), так как гармонический ряд расходится.

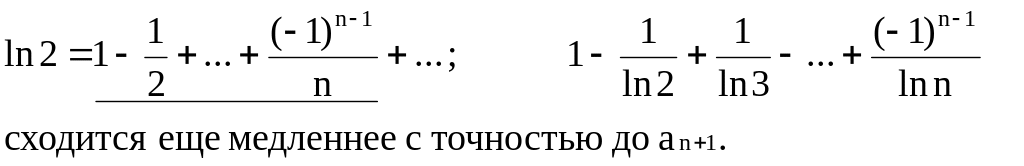
Пример (расходящийся знакочередующийся ряд):

не монотонно: расходится.

Вообще, если ряд представим в виде суммы рядов:

1. Если оба ряда сходятся, то их сумма сходится.

2. Если один из рядов сходится, а другой расходится, то их сумма расходится.

Признак Дирихле.

Пусть дан ряд:

тогда сходится.

Доказательство: По критерию Коши: .

по условию

Используя преобразование Абеля, получим неравенство:

Следовательно, критерий Коши выполнен, поэтому ряд сходится.

Из признака Дирихле следует признак Лейбница:

Если .

Признак Абеля.

; тогда сходится

Доказательство:

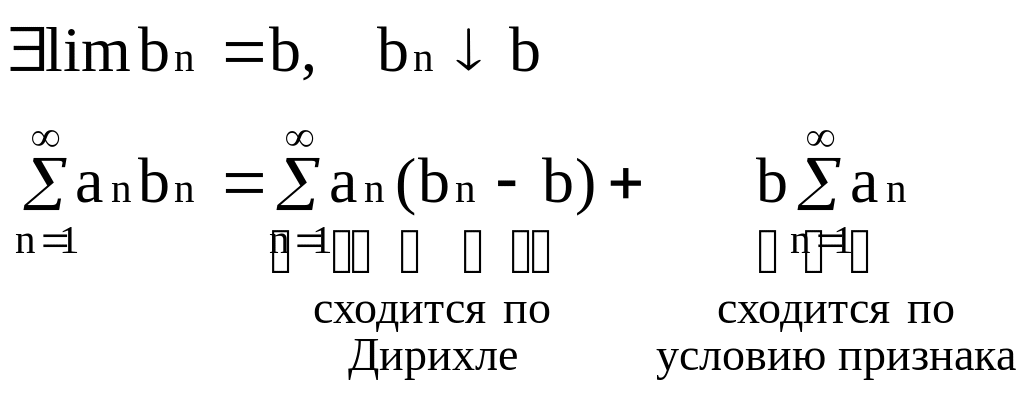Доказано.

Пример 1:

:

Докажем, что эти ряды сходятся условно:

Докажем, что ряд расходится. Так как , рассмотрим следующий ряд:

.

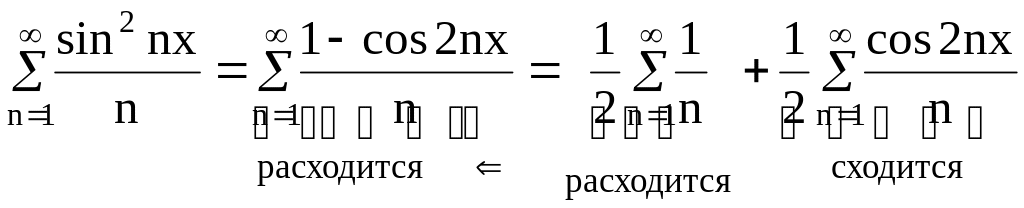Значит, ряд

Пример 2:

При произвольной перестановке членов условно сходящегося ряда его сумма может изменяться:

;

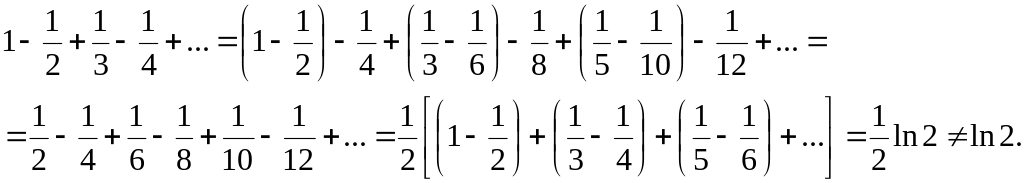
Теорема Римана (без доказательства).

Теорема: Пусть дан условно сходящийся ряд . Тогда: перестановка слагаемых, такая, что

Теорема Дирихле о перестановке членов абсолютно сходящегося числового ряда.

Теорема: Пусть ряд сходится абсолютно, . Тогда, для любой перестановки ряда новый ряд сходится. При этом, ряд A сходится абсолютно и его сумма равна сумме исходного ряда, то есть A = A.

Доказательство:

1)

k – фикс., , тогда

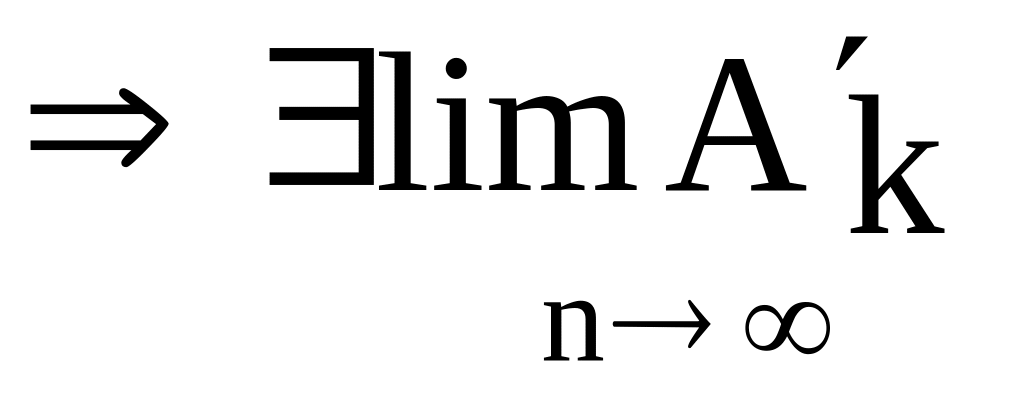
и .

Аналогично рассматривается ряд А, как полученный перестановкой

членов :

.

Доказано.

2) a_n – произвольного знака. Пусть тогда:

;

– сходится, – сходится, так как ряд A сходится абсолютно .

Применяя к и результат из 1), получим полное доказательство.

Доказано.

Функциональные ряды

– функциональные ряды, f_n(x), f(x) – функции от , где D – область сходимости ряда.

Примеры функциональных рядов:

1) – степенной ряд

2) – тригонометрический ряд Фурье

Равномерная сходимость функциональной последовательности и функционального ряда.

Определение (равномерной последовательности на множестве E D функциональной последовательности):

Пример:

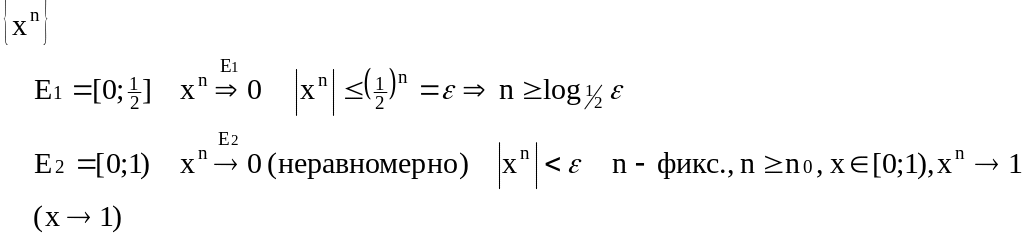
Критерий Коши:

Определение равномерной сходимости функционального ряда на множестве E:

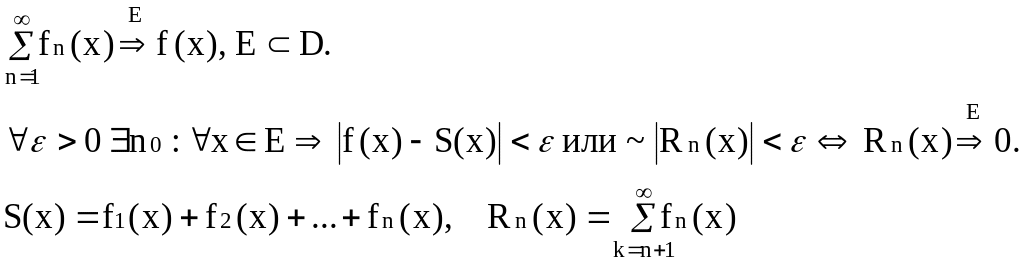
Критерий Коши:

.

Следствие. Если

Примеры: 1)

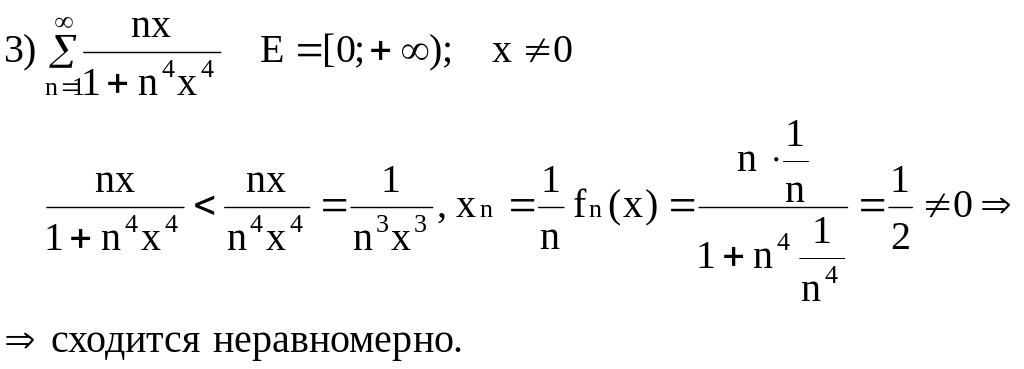
Признак равномерной сходимости.

1) Признак Вейерштрасса (мажорантный признак)

Пусть дан функциональный ряд и если – сходится, то функциональный ряд сходится равномерно на E.

Доказательство (по критерию Коши):

, так как и

Примеры:

К ряду – признак Вейерштрасса неприменим.