
Яблонский Д3 вариант 10
.doc
З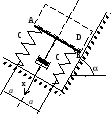 АДАНИЕ
Д3-10
АДАНИЕ
Д3-10
Дано:
![]() =
1 кг,
=
1 кг,
![]() =
1,5 Н/см,
=
1,5 Н/см,
![]() Н,
Н,
![]() =60о.
=60о.
Найти: уравнение движения груза D относительно оси х
РЕШЕНИЕ:
1. Заменим систему из пружин
1, 2 одной с эквивалентной жесткостью
![]() .
При параллельном соединении пружин 1 и
2
.
При параллельном соединении пружин 1 и
2
![]() =3
(Н/см).
=3
(Н/см).
2. Рассмотрим движение груза
D под
действием пружины с жесткостью
![]() =
300 Н/м. Совместим начало координат с
концом недеформированной пружины.
=
300 Н/м. Совместим начало координат с
концом недеформированной пружины.
Здесь
![]() – статическая деформация пружины под
действием груза массой
– статическая деформация пружины под
действием груза массой
![]() ;
;
В состоянии покоя сила тяжести
уравновешивается силой упругости
пружины
состоянии покоя сила тяжести
уравновешивается силой упругости
пружины
![]() или
или
![]() . (1)
. (1)
3. Составим дифф. уравнение
движения груза в виде ![]() .
На тело действуют сила тяжести
.
На тело действуют сила тяжести
![]() ,
сила сопротивления
,
сила сопротивления
![]() и сила упругости пружины
и сила упругости пружины
![]() .
. ![]() ,
, ![]() .
С учетом уравнения (1)
.
С учетом уравнения (1)
![]() или
или ![]() .
.
![]() =
=![]() =300
(1/с2).
=300
(1/с2).
![]() (2)
(2)
3. Для определения закона
движения груза найдем решение однородного
дифференциального уравнения (2): для его
нахождения решаем характеристическое
уравнение
![]() ,
, ![]() .
Тогда
.
Тогда
![]() , (3)
, (3)
Для определения постоянных интегрирования найдем еще
![]() . (4)
. (4)
Используем начальные условия
задачи. Рассматриваемое движение
начинается тогда, когда деформация
пружины равна статической деформации
под действием только груза D.
При принятом положении начала отсчета
начальная координата груза D
равна:
![]() (м).
(м).
![]() =0.
Из уравнений (3) и (4) найдем
=0.
Из уравнений (3) и (4) найдем
![]() и
и
![]()
![]()
![]()
![]()
![]() .
Следовательно, уравнение движения груза
.
Следовательно, уравнение движения груза
![]()
