Чернова Н.И. Лекции по математической статистике

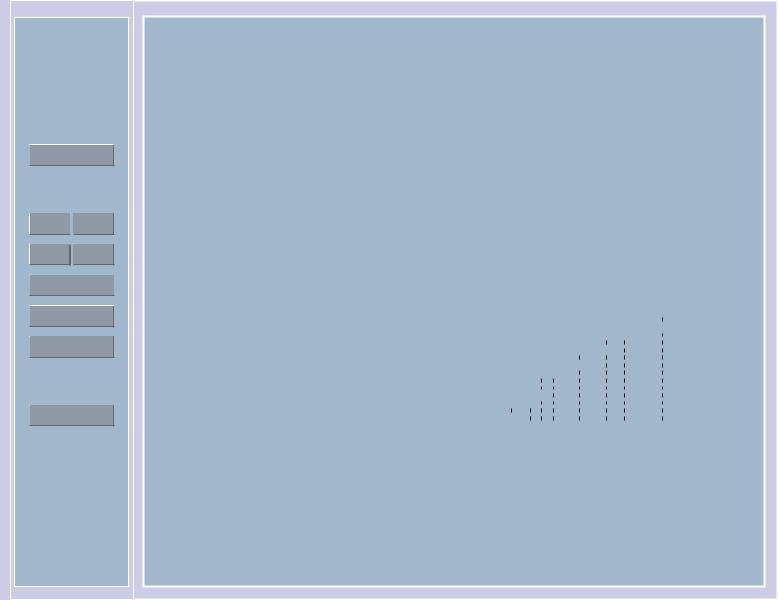
Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 11

Если элементы выборки X1, . . . , Xn упорядочить по возрастанию (на каждом элементарном исходе), получится новый набор случайных величин, называемый вариационным рядом:

X(1) 6 X(2) 6 . . . 6 X(n−1) 6 X(n).

Здесь

X(1) = min{X1, . . . , Xn}, X(n) = max{X1, . . . , Xn}.

Элемент X(k), k = 1, . . . , n называется k-м членом вариационного ряда или k-й порядковой статистикой.

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 12

Другой характеристикой распределения является таблица (для дискретных распределений) или плотность (для абсолютно непрерывных). Эмпирическим, или выборочным аналогом таблицы или плотности является так называемая гистограмма.

Гистограмма строится по группированным данным. Предполагаемую область значений случайной величины ξ (или область выборочных данных) делят независимо от выборки на некоторое количество интервалов (не обязательно одинаковых). Пусть A1,

. . . , Ak — интервалы на прямой, называемые интервалами группировки. Обозначим для j = 1, . . . , k через νj число элементов выборки, попавших в интервал Aj:

На каждом из интервалов Aj строят прямоугольник, площадь которого пропорциональна νj. Общая площадь всех прямоугольников должна равняться единице. Пусть lj — длина интервала Aj. Высота fj прямоугольника над Aj равна

fj = νj . nlj

Полученная фигура называется гистограммой.

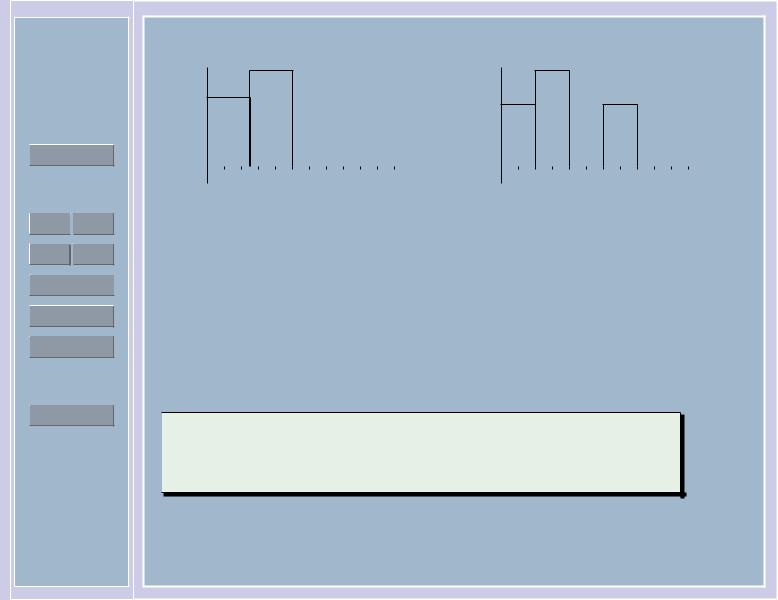
Пример 2. Имеется вариационный ряд (см. пример 1):

(0; 1; 1; 2; 2,6; 2,6; 2,6; 3,1; 4,6; 4,6; 6; 6; 7; 9; 9).

Разобьем отрезок [0, 10] на 4 равных отрезка. В отрезок A1 = [0; 2,5) попали 4 элемента выборки, в A2 = [2,5; 5) — 6, в A3 = [5; 7,5) — 3, и в отрезок A4 = [7,5; 10] попали 2 элемента выборки. Строим гистограмму (рис. 2). На рис. 3 — тоже гистограмма для той же выборки, но при разбиении области на 5 равных отрезков.

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 13

8/75

0.1

Замечание 1. В курсе «Эконометрика» утверждается, что наилучшим числом интервалов группировки («формула Стерджесса») является k = k(n) = 1 + [3.322 lg n].

Здесь lg n — десятичный логарифм, поэтому k = 1+[log2 10 log10 n] = 1+[log2 n], т. е. при увеличении выборки вдвое число интервалов группировки увеличивается на 1.

Заметим, что чем больше интервалов группировки, тем лучше. Но, если брать число интервалов, скажем, порядка n, то с ростом n гистограмма не будет приближаться к плотности.

Справедливо следующее утверждение:

Если плотность распределения элементов выборки является непрерывной функцией, то при k(n) → ∞ так, что k(n)/n → 0, имеет место поточечная сходимость по вероятности гистограммы к плотности.

Так что выбор логарифма разумен, но не является единственно возможным.

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 14

1.4.Выборочные моменты

Знание моментов распределения также многое может сказать о его виде и свойствах. Введем выборочные аналоги неизвестных истинных моментов распределения.

Пусть E ξ = E X1 = a, D ξ = D X1 = σ2, E ξk = E Xk1 = mk — теоретические среднее, дисперсия, k-й момент. Мы уже знакомы с соответствующими характеристи-

ками выборочного распределения E ξ = X, D ξ = S2, E (ξ )k = Xk.

Список числовых характеристик и их оценок можно продолжать, рассмотрев, например, центральные, абсолютные и т. п. моменты. В общем случае

=

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 15

1.5.Сходимость эмпирических характеристик к теоретическим

Мы ввели три вида эмпирических характеристик, предназначенных для оценивания неизвестных теоретических характеристик распределения: эмпирическую функцию распределения, гистограмму, выборочные моменты. Если наши оценки удачны, разница между ними и истинными характеристиками должна стремится к нулю с ростом объема выборки. Такое свойство эмпирических характеристик называют состоятельностью. Убедимся, что наши выборочные характеристики таким свойством обладают.

1.5.1.Свойства эмпирической функции распределения

Теорема 1. Пусть X = (X1, . . . , Xn) — выборка объема n из неизвестного распределения F с функцией распределения F. Пусть Fn — эмпирическая функция распределения, построенная по этой выборке. Тогда для любого y IR

Замечание 2. Fn(y) — случайная величина, так как она является функцией от случайных величин X1, . . . , Xn. То же самое можно сказать про гистограмму и выборочные моменты.

Доказательство теоремы 1. По определению 1,

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 16

Случайные величины I(X1 < y), I(X2 < y), . . . независимы и одинаково распределены, их математическое ожидание конечно:

E I(X1 < y) = 1 · P (X1 < y) + 0 · P (X1 > y) = P (X1 < y) = F(y) < ∞,

поэтому применим´ ЗБЧ Хинчина, а что это такое? и

n

I(Xi < y)

сходится (по вероятности) к неизвестной теоретической.

Верен более общий результат, показывающий, что сходимость эмпирической функции распределения к теоретической имеет «равномерный» характер.

Теорема Гливенко — Кантелли. Пусть X = (X1, . . . , Xn) — выборка объема n из неизвестного распределения F с функцией распределения F. Пусть Fn — эмпирическая функция распределения, построенная по этой выборке. Тогда

Замечание 3. Более того, в условиях теорем 1 и Гливенко — Кантелли имеет место сходимость не только по вероятности, но и почти наверное.

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 17

Если функция распределения F непрерывна, то скорость сходимости к нулю в тео-

√

реме Гливенко — Кантелли имеет порядок 1/ n:

Теорема Колмогорова. Пусть X = (X1, . . . , Xn) — выборка объема n из неизвестного распределения F с непрерывной функцией распределения F, а Fn — эмпирическая функция распределения. Тогда

где случайная величина η имеет распределение Колмогорова с непрерывной функцией распределения

Следующие свойства эмпирической функции распределения — это хорошо знакомые нам свойства среднего арифметического n независимых слагаемых, имеющих, к тому же, распределение Бернулли.

В первых двух пунктах утверждается, что случайная величина Fn(y) имеет ма-

тематическое ожидание F(y) и дисперсию F(y)(1 − F(y)) , которая убывает как 1/n. n √

Третий пункт показывает, что Fn(y) сходится к F(y) со скоростью 1/ n.

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 18

—«асимптотически нормальная» оценка для F(y);

4)случайная величина n · Fn(y) имеет биномиальное распределение Bn,F(y).

Доказательство свойства 1. Заметим снова, что I(X1 < y) имеет распределение Бернулли BF(y), поэтому

E I(X1 < y) = F(y) и D I(X1 < y) = F(y)(1 − F(y)).

1) Случайные величины I(X1 < y), I(X2 < y), . . . одинаково распределены, поэтому

где используется одинаковая распределенность?

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 19

2) Случайные величины I(X1 < y), I(X2 < y), . . . независимы и одинаково распреде- лены, поэтому где используется независимость?

Замечание 4. Все определения, как то: «оценка», «несмещенность», «состоятельность», «асимптотическая нормальность» будут даны в главе 2. Но смысл этих терминов должен быть вполне понятен уже сейчас.

Оглавление

JJ II

J I

На стр. ... из 179

Назад

Во весь экран

Уйти

Стр. 20

1.5.2. Свойства гистограммы

Пусть распределение F абсолютно непрерывно, f — его истинная плотность. Пусть, кроме того, число k интервалов группировки не зависит от n. Случай, когда k = k(n), отмечен в замечании 1.

Справедлива

Теорема 2. При n → ∞ для любого j = 1, . . . , k

Упражнение. Доказать теорему 2, используя (1) и ЗБЧ.

Теорема утверждает, что площадь столбца гистограммы, построенного над интервалом группировки, с ростом объема выборки сближается с площадью области под графиком плотности над этим же интервалом.