Практика 5 Примеры задач оптимизации в экономике и финансах

Теория.

1. Функция полезности с полным взаимозамещением благ:

где коэффициент является числовой оценкой полезности от потребления единицы товара вида i.

2. Функция полезности с полным взаимодополнением благ:

где - количество товара вида i, приходящееся на единицу полезности. Для построения кривых безразличия функции в из уравнения найдем

если (1)

если (2)

если (3)

3. Задача потребительского выбора. Задача потребительского выбора имеет вид: при ограничении и условие .

Решение задачи потребительского выбора: либо графический метод решения задач линейного программирования, либо метод Лагранжа. Решением задачи является набор .

4. Эластичность спроса по цене. Коэффициент ценовой эластичности спро­са: процентного изменения количества спрашиваемой продукции к процентному изменению цены, вызвавшему это изменение спроса , где , тогда :

Q₁ и Q₂ — первоначальный и текущий объем спроса;

P₁ и Р₂ — первоначальная и текущая цена.

Фор­мула центральной точки:

Пример 1.

Пусть товаром первого вида является кофе, второго – чай, а потребление этих продуктов в количествах и дает полезность, равную с , то есть .

Представим, что потребление кофе уменьшилось на единиц. Тогда полезность упадет до уровня . Чтобы компенсировать эту потерю полезности надо увеличить потребление чая на величину так, чтобы

В результате имеем:

Отсюда найдем .

Таким образом, функция позволяет определить размер замещения одних товаров другими для того, чтобы полезность оставалась на неизменном уровне.

Пример 2.

Приобретается набор из двух товаров: кофе в количестве и сахара в количестве c . Потребление этих товаров дает полезность, равную с, то есть

В случае (1)

и увеличение (уменьшение) потребления кофе влечет увеличения (уменьшения) сахара.

В случае (2) увеличение потребления кофе может привести к нарушению неравенства в (2) и, следовательно, к нарушению уровня полезности, если не увеличиться потребление сахара.

Функция (2) применяется для определения полезности набора взаимодополняющих друг друга товаров.

Пример 3.

Оптимальный набор потребителя составляет 6 ед. продукта х₁ и 8 ед. продукта . Определите цены потребляемых благ, если известно, что доход потребителя равен 240 руб. Функция полезности потребителя имеет вид: u(x₁,x₂)= .

Решение. Следуя принципу решения, получаем систему уравнений:

,

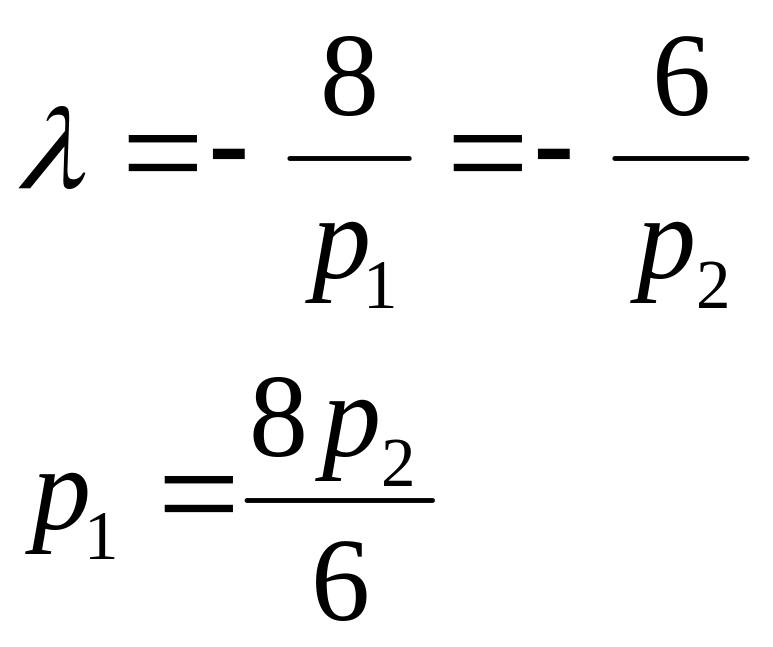
16p₂=240 p₂=15 p₁=20

Подставив, вместо х₁ - 6 ед., вместо х₂ - 8 ед., получим: p₁=20руб., p₂=15руб.

Итак, решение задачи потребительского выбора сводится к решению задач на условный экстремум.

Пример 4.

Цена товара колеблется в интервале от 4 до 5 ден. ед. При P_x=4 ден. ед. объем спроса составляет 4000 ед. продукции. При P_x = 5 ден. ед. — 2000 ед. Используя первоначальную формулу

рассчитаем значение коэффициента ценовой эластичности для данного ценового интервала:

Однако если в качестве базовой взять другую комбинацию цены и количества продукции, то получим:

И в первом, и во втором случае спрос эластичный, но ре­зультаты отражают разную степень эластичности, хотя анализ мы проводим на одном и том же ценовом интервале. Для пре­одоления этого затруднения экономисты используют в качестве базовых средние величины уровней цены и количеств, т. е.

или