Термодинамика. Лекция 7.

К.т.н. Прохоренко Н.Н.

Обратные термодинамические циклы и холодильные установки.

Термодинамика получения холода. Холодильные установки, их

классификация и области применения в химической технологии.

В лекции 4 рассмотрены прямые и обратные циклы, введены показатели эффективности их в виде термического коэффициента полезного действия для прямых циклов и в виде холодильного коэффициента для обратных циклов. Напомним, что и в том, и в другом случае эффективность цикла представляет собой отношение «пользы» к «затратам». Для тепловых циклов «пользой» является получаемая работа, а «затратами» - количество теплоты, подводимой в цикле. Для обратного, т.е. холодильного цикла, «пользой» является количество отводимой теплоты (холода) из холодильной камеры в рабочее тело (хладоагент), а «затратами» будут количество работы из внешней среды.

Назначение холодильных установок – достижение или поддержание низких температур (по сравнению с температурой окружающей среды (атмосферы)) рабочих тел в циклах.

Классификация холодильных установок осуществляется по уровню достигаемой температуры. Различают установки умеренного холода и глубокого холода. Границей между ними приняли температуру 120К.

При использовании установок умеренного холода ставится лишь одна технологическая задача – создание и поддержание низкой температуры в холодильной камере. В ней химики-технологи реализуют необходимые им процессы химических и фазовых превращений (например, экзотермические реакции). В быту в холодильной камере размещают продукты питания, чтобы избежать их порчи.

Установки глубокого холода предназначены для производства жидкой фазы из газообразной. Установки ожижения воздуха позволяют получить жидкую фазу, которая далее идет на разделение с целью получения чистого кислорода и азота и комплекта инертных газов. Первый предназначен для металлургических процессов, второй – для производства азотной кислоты. Природный газ также ожижают с целью отделения гелия и для дальнейшей транспортировки в жидком состоянии.

1. Методы достижения низких температур.

Оказывается, существует свыше 200 технологических приемов достижения низких температур, среди которых самыми распространенными в промышленности не тепловыми методами являются использование дросселирования газа и его адиабатное расширение.

0. Дросселирование, как способ понижения температуры.

В общих чертах процесс дросселирования рассматривался в лекции 5. В ней этот процесс представлен был как предельный случай течения газовых сред в каналах с большими скоростями. Предельность заключалась в том, что вся работа проталкивания через малое отверстие тратится на необратимый процесс роста энтропии. Так как теплота диссипации остается в самом потоке, то инвариантом процесса дросселирования является величина энтальпии: h = const. В той же лекции 5 показано, что давление в процессе уменьшается, удельный объем, соответственно, увеличивается, энтропия растет. Зато вопрос об изменении температуры остался открытым.

Займемся этим вопросом сейчас. По существу речь идет о знаке

(∂T/∂p)_h ,

причем в этой частной производной определенно знаем, что знак знаменателя отрицателен. Следовательно, если определим знак самой производной, то найдем знак ее числителя, т.е. узнаем характер изменения температуры в процессе: растет или убывает.

Выше в наших лекциях было показано, что для реальных веществ

dh = Tds + vdp, dh = c_pdT – (T(∂v/∂T)_p – v)dp. (7.1)

Для дросселирования h = const, т.е. dh = 0, поэтому

0 = c_pdT – (T(∂v/∂T)_p – v)dp.

Разделим обе части этого уравнения на dp (еще раз подчеркнем, что dp < 0) и будем помнить, что h = const, т.е.

(∂T/∂p)_h = 1/c_p [T(∂v/∂T)_p – v] или (∂T/∂p)_h = T/c_p [(∂v/∂T)_p – v/T] = α_h. (7.2)

Величина α_h в термодинамике носит название дифференциального дроссельэффекта Джоуля – Томсона. Знак этой величины по существу и определяет знак приращения ΔT при дросселировании. Рассмотрим рис. 7.1.

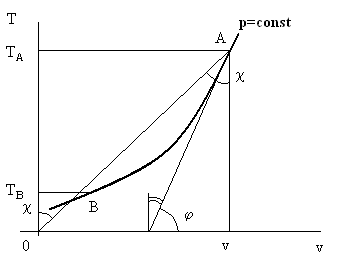
Рис. 7.1. К определению знака изменения температуры при дросселировании.

На рис 7.1 изображена изобара p = const в осях T – v. Для реальных веществ ее, как правило, строят экспериментально. Рассматривается точка А на изобаре. Эта точка характеризует состояние реального рабочего тела далеко от самого дросселя (т.е. резкого сужения или малого отверстия в мембране поперек трубы, по которой происходит течение газа). Ставится вопрос: температура за дросселем станет больше или меньше температуры в точке А? Глядя на формулу (7.2), видно, что T > 0 всегда, с_р > 0 тоже. Следовательно, знак α_h определяется знаком выражения в квадратных скобках. Найдем его для точки А. Проводим касательную к изобаре в точке А. Тогда tgφ = (∂T/∂v)_p. В соответствии с теоремой о производной обратной функции tg(π/2 – φ) = (∂v/∂T)_p.

Далее, соединим точку А с началом системы координат О и рассмотрим прямоугольный треугольник ОАv. Отношение v/T (см.(7.2)) есть tgæ, причем угол æ накрест лежащий углу АОТ_А и, следовательно, ему равный.

Сравнивая величину углов π/2 – φ и æ видно, что первый угол меньше второго, следовательно, (∂v/∂T)_h в точке А на рис.7.1 меньше, чем отношение v/T в той же точке. Следовательно, выражение в квадратной скобке в формуле (7.2) отрицательно, тогда и α_h < 0 и, окончательно, приращение температуры после дросселирования положительно. Иными словами, если до дросселя была температура T_А, то после дросселя будет большая температура.

Рассматривая рис. 7.1 и проводя аналогичные построения, можно доказать, что, если до дросселя была температура T_В (см. точку В на рис. 7.1), то после процесса дросселирования температура рабочего тела уменьшится.

Если при дросселировании из точки А температура увеличивается, а при дросселировании из точки В уменьшается, то должна существовать точка С на изобаре, при дросселировании из которой температура не изменится. И действительно, проведя из начала координат О прямую, касательную к изобаре, получим точку С (см. рис. 7.2) В ней

(∂v/∂T)_h = v/T,

тогда α_h = (∂T/∂p)_h = 0 и, следовательно, T = const.

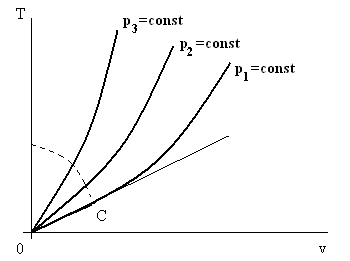
Рис. 7.2. Иллюстрация к определению точки инверсии и линии инверсии.

Линия инверсии изображена пунктиром.

Определение. Состояние рабочего тела до процесса дросселирования, при котором после этого процесса температура не изменяется, называется состоянием инверсии, а сама точка, характеризующая это состояние, называется точкой инверсии.

Согласно этому определению точка С на рис. 7.2 является точкой инверсии. Если в координатах T – v изобразить пучок изобар, на каждой найти точку инверсии и все эти точки соединить плавной линией, то получим геометрическое место точек инверсии (см. пунктирную линию на рис. 7.2). Если дросселировать рассматриваемое вещество из состояний, точки которых расположены правее и выше линии инверсии, то температура рабочего тела после дросселя обязательно будет выше температуры до дросселя. Если эти точки будут располагаться ниже линии инверсии, то – ниже.

Рассмотрим частные случаи.

1. Пусть рабочим телом при дросселировании является идеальный газ. Найдем величину (∂v/∂T)_h, пользуясь уравнением состояния pv = RT. Тогда v = RT/p и (∂v/∂T)_p = R/p = v/T. Выражение в квадратных скобках в (7.2) станет 0 и α_h = 0. Следовательно, при дросселировании идеального газа его температура не меняется.

2. Пусть рабочим телом при дросселировании является влажный пар какого-нибудь реального вещества. В лекции 2 предлагалось студентам потренироваться и получить все дифференциальные соотношения технической термодинамики. Послушные студенты могли бы получить соотношение

(∂p/∂T)_v = (∂s/∂v)_T или (∂T/∂p)_v = (∂v/∂s)_T. (7.3)

Для процесса дросселирования хотим найти (∂T/∂p)_h. Но в области влажного пара любого вещества давление насыщенного пара зависит только от температуры (см. лекцию 3). Тогда (∂T/∂p)_h = dT/dp. Следовательно, диффсоотношение (7.3) примет вид

dT/dp = (∂v/∂s)_T =(v΄΄ - v΄)dx /(s΄΄ - s΄)dx = (v΄΄ - v΄)/(s΄΄ - s΄).

Напомним, что величины с двумя штрихами относятся к параметрам состояния сухого насыщенного пара, а величины с одним штрихом – к кипящей жидкости (см. лекцию 3). Величина dx – просто дифференциал степени сухости х влажного пара (опять-таки см. лекцию 3)

В последнем выражении справа умножим числитель и знаменатель дроби на величину T. Тогда

dT/dp = T(v΄΄ - v΄)/r ≈ Tv΄΄/r > 0. (7.4)

Снова напомним, что T(s΄΄-s΄) = r, т.е. теплоте фазового перехода (см. лекцию 3).

Строгое равенство в (7.4) в термодинамике называют уравнением Клайперона – Клаузиуса. Из него следует, что при очевидном обстоятельстве v΄΄>> v΄(примерно в 1000 раз) dT/dp всегда строго больше 0. Окончательный вывод: при дросселировании влажного пара любого вещества температура пара после дросселя только уменьшается.

Замечание. Здесь получен очень важный и общий физический результат. Он был бы невозможен без такого термодинамического инструмента, как дифференциальные соотношения термодинамики.