4. Реальное течение пара или газа по каналам.

Рассмотренное выше движение газа (пара) по каналам различной формы происходило в условиях адиабатно-изоэнтропийного процесса (см. предпосылки построения термодинамической модели процесса течения). Это возможно в идеальных условиях отсутствия трения и теплообмена с внешней средой. В реальных течениях поток взаимодействует со стенкой канала, а высокая температура потока неизбежно ведет к теплопередаче с окружающей средой.

Последнее обстоятельство является предметом специального курса «Теплообмен», в рамках дисциплины «Процессы и аппараты химической технологии», и мы его касаться не будем.

Трение возникает по причине шероховатости внутренней поверхности канала и вязкости рабочего тела (свойство вещества). При движении по каналу в месте контакта с поверхностью поток полностью теряет скорость (w = 0), возникает профиль скорости по радиусу канала с максимумом на оси симметрии канала. В термодинамике такие детали не рассматриваются, а скорость потока принимается постоянной по радиусу и равной

w = 4Gv/πd² м/с,

где G – массовый расход среды кг/с, d – диаметр канала в данном сечении, м. И вся работа трения условно сносится на поверхность контакта потока со стенкой канала. Тогда схема термодинамической системы для реальных течений сводится к взаимодействию потока с окружающей средой, т.е. стенкой канала + атмосферой.

Для неподвижного канала (δl_технич = 0) применимо уравнение (5.1 – в)

du + d(w²/2) = δq – δl_потока – δl_трения (5.14)

Напомним, что работа трения полностью диссипирует, т.е. обращается в тепловую энергию, которую поток (а он не различает причину) воспринимает как подвод теплоты из окружающей среды: l_трения = q_трения.

Уравнение энергии потока без учета теплообмена получает следующий вид:

dw²/2 + dh + δl_трения = 0, (5.15)

и, если считать начальную скорость потока (на входе в канал) нулевой, то получаем

w = [2(h₁ – h_трения)]^1/2. (5.16)

В этой формуле величина энтальпии h_трения рассчитывается по эмпирическим данным следующим образом:

h_трения = h_s + Δ_трения, (5.17)

где h_s – величина энтальпии в конечной точке идеального процесса течения при s = const, а Δ_трения – потери энтальпии на работу трения. Эта величина рассчитывается как

Δ_трения = w²/2 (1 – φ²) = (h₁ – h₂)(1 – φ²). (5.18)

Здесь φ – коэффициент скорости, φ ≡ w_трения/w_s, является опытной или справочной величиной для данного канала.

Р

Дросселирование – процесс 1-4 h=const

ассмотрим рис 5.14, на котором изображена диаграмма h – s и процесс течения с трением.

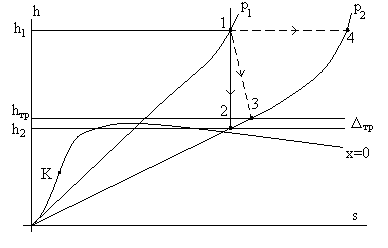
Рис. 5.14. Иллюстрация к расчету скорости в канале с учетом трения.

Из рис. 5.14 следует, что точка 3 находится на изобаре р₂ = const и она расположена правее точки 2 согласно 2 – му закону термодинамики (Δs_диссип = s₃ – s₂ > 0).

5.1. Дросселирование.

При встрече потока с сужением (вентиль, капилляр, мембрана с малым отверстием на оси и т.п.) потери на трение максимальны. Работа трения переходит в теплоту и вся эта теплота остается в потоке. Поэтому такой процесс (его называют дросселированием или мятием) имеет инвариант h = const. Наверное, понятно из рис. 5.14 (см. процесс 1 – 4 (пунктир)), что при дросселировании давление уменьшается (dp < 0), удельный объем вещества в потоке соответственно растет (dv > 0), энтропия обязательно увеличивается (ds > 0). А вот об изменении температуры потока поговорим в лекции 7.

Пример 4. Пар движется по конфузору в условиях примера 3, но с трением при известном коэффициенте скорости φ = 0,93. Найти реальную скорость пара на выходе из конфузора.

Решение. Потери энтальпии на трение рассчитываются по формуле (5.18):

Δ_трения = (h₁ – h_k)(1 – φ²) = (3128 – 2944)(1 – 0,93²) = 25 кДж/кг.

Величина энтальпии пара на выходе из конфузора (точка 3 на рис. 5.14) равна:

h_трения = h_k + Δ_трения = 2944 + 25 = 2969 кДж/кг.

Реальная скорость истечения пара из конфузора:

w₃ = [2(3128 – 2969)10³]^1/2 = 564 м/с (а было w₂ = 607 м/с).

Ответ: скорость истечения пара из конфузора w₃ = 564 м/с.

Пример 5. В цехе химического завода со взрывоопасными условиями работы приводом для компрессора является паровая турбина с питанием перегретым паром с давлением р = 5 бар, а заводская котельная производит пар с давлением 15 бар и температурой 240⁰С. Как трансформировать котельный пар и сделать его пригодным для паровой турбины?

Решение. Один из способов трансформации (не единственный) – подвергнуть пар из котельной мятию (дросселированию) (см. рис. 5.14, процесс 1 – 4).

По диаграмме h – s для водяного пара находим параметры состояния в точке 1. Сама точка 1 находится на пересечении изобары р₁ = 15 бар и изотермы Т₁ = 240⁰С. Считываем с диаграммы для точки 1 величину энтальпии h₁ = 2898 кДж/кг.

Точка 4 (см. рис. 5.14) находится на пересечении линии h = const = 2898 кДж/кг и изобары р₂ = 5 бар. Опять с диаграммы считываем величину температуры Т₂ = 225⁰С.

Ответ: можно применить процесс дросселирования до давления р₂ = 5 бар. Получится перегретый пар, пригодный для питания турбины.

Замечание. Конечно, такое решение проблемы обрадует заводчан своей простотой и отсутствием специальной обслуги «трансформации» пара. Но решение очень не экономичное: из хорошего и дорогого пара сделали пар с большой энтропией, себестоимость целевого продукта химического завода такое решение только увеличит.