
- •Лабораторная работа №1 Методы преобразования цифровых изображений
- •Векторные и растровые изображения.
- •Форматы
- •Цветовые пространства
- •Цветовое пространство rgb
- •Цветовое пространство xyz
- •Цветовое пространство lab.
- •Цветовое пространство yСrCb
- •Цветовое пространство hsv
- •Преобразование цветного изображения в градациях серого
Лабораторная работа №1 Методы преобразования цифровых изображений
1. Цель роботы
Изучение основных форматов цифровых изображений и цветовых пространств. Преобразования цветного изображения в градации серого.
2. Ключевые понятия
Оптическое
изображение с точки зрения теории
сигналов является двумерным непрерывным
сигналом. В таком виде оно не пригодно
для обработки в компьютерных системах,
и, следовательно, должно быть преобразовано.
Для того чтобы преобразовать изображение
из аналоговой формы в цифровую необходимо
выполнить две процедуры: дискретизацию
(по пространственным координатам) и
квантование (по интенсивности). Пусть
изображение описывается функцией
![]() ,
где
,
где
![]() – координаты в плоскости изображения,
имеющие мощность множества действительных
чисел, при этом их называют непрерывными,
а значение
– координаты в плоскости изображения,
имеющие мощность множества действительных
чисел, при этом их называют непрерывными,
а значение
![]() – характеристика цвета или яркость
точки изображения с координатами
.
В общем случае, дискретизация заключается
в переходе от координат
– характеристика цвета или яркость
точки изображения с координатами
.
В общем случае, дискретизация заключается
в переходе от координат
![]() ,
которые являются действительными
числами, к новым координатам
,
которые являются действительными
числами, к новым координатам
![]() ,
которые являются целыми числами. При
этом функция
заменяется множеством значений
,
которые являются целыми числами. При
этом функция
заменяется множеством значений
![]() ,
которые называются отсчетами. В свою
очередь квантования заключается в
замене множества значений
,
которая является множеством действительных
чисел, дискретной конечное множество
характеристик цвета или яркости
дискретного элемента изображения
,
которые называются отсчетами. В свою
очередь квантования заключается в
замене множества значений
,
которая является множеством действительных
чисел, дискретной конечное множество
характеристик цвета или яркости
дискретного элемента изображения
![]() ,
где
,
где
![]() .
После выполнения процедур дискретизации
и квантования получают изображения в
цифровой форме. Рассмотрим процедуры
дискретизации и квантования более
детально.
.
После выполнения процедур дискретизации
и квантования получают изображения в
цифровой форме. Рассмотрим процедуры
дискретизации и квантования более
детально.
Дискретизацию
аналогового изображения можно выполнить
различными методами, например, с
использованием интегральных преобразований.
На практике используется периодическая
дискретизация, которая заключается в
следующем. Выбирается шаг дискретизации
по каждой из координат:
![]() и
и
![]() .
Потом изображение «разбивается» на
отдельные
элементы, как это схематически представлено
на рис. 1.
.
Потом изображение «разбивается» на
отдельные
элементы, как это схематически представлено
на рис. 1.
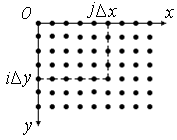 Рисунок
1 – Отсчеты
прямоугольной периодической дискретизации
Рисунок
1 – Отсчеты
прямоугольной периодической дискретизации
Соответствие
между отсчетом цвета
![]() и функцией
и функцией
![]() определяется равенством.
определяется равенством.
![]() .
.
Решетку, которую получают в результате дискретизации называют растром. Элементы растра (отсчеты) принято называть пикселями. Это название происходит от английского термина "pixel", что является сокращением слов picture element - элемент рисунка, изображения.
От величины шагов дискретизации зависит разрешение дискретизованого изображения, которую принято определять как количество пикселей в одном дюйме (1 дюйм равен 2,53 см), которые обозначают аббревиатурой ppi - pixels per inch. Например, разрешение 60 ppi означает, что в одном дюйме содержится 60 точек. От разрешения зависит качество воспроизведения дискретизированого изображения. Проиллюстрируем это на примере дискретизации изображения треугольника при условии, что его размеры 1 × 1 дюйм.
Из приведенных рисунков следует, что чем больше разрешение, тем меньше различий между реальным и дискретизированым изображениями
 а) б) в)
а) б) в)
Рисунок 2 – Дискретизация с разной разрешением а) оригинальное изображение, б, в) дискретизированые изображения с распределительными способностями в 4 и 8 ррі.
Конечно,
нельзя как угодно увеличивать разрешение,
поэтому возникает вопрос определения
условий по выбору оптимального шага
дискретизации. Эти условия можно
получить, если рассматривать
![]() как двухмерный сигнал
как двухмерный сигнал
![]() с ограниченным частотным спектром:
с ограниченным частотным спектром:
![]() ,
,
![]() .
Тогда, согласно теореме Котельникова,
шаг дискретизации должен удовлетворять
условия:
.
Тогда, согласно теореме Котельникова,
шаг дискретизации должен удовлетворять
условия:
![]() ,
,
![]() .
.
Выполнение этих условий обеспечивает максимальное качество дискретизированого изображения и минимизирует ошибку воспроизведения аналогового изображения с дискретизированого.
При
цифровой обработке
изображений диапазон характеристик
цвета или яркости разделяется на ряд
дискретных уровней. Эта
процедура называется квантованием.
Рассмотрим
процедуру квантования на примере функции
одной переменной
![]() .
Квантования
этой функции состоит из следующих шагов.
Сначала множество ее значений, в
простейшем случае, разбивается на
.
Квантования
этой функции состоит из следующих шагов.
Сначала множество ее значений, в
простейшем случае, разбивается на
![]() диапазонов
диапазонов
![]() ,
,
![]() .
.
Каждому из этих
диапазонов назначается соответствующий
уровень квантования
![]() .
Тогда значения функции
.
Тогда значения функции
![]() заменяется
на соответствующий уровень квантования
(смотр. рис. 3). При равномерном квантовании,
диапазоны и уровни определяются с
использованием соотношений
заменяется
на соответствующий уровень квантования
(смотр. рис. 3). При равномерном квантовании,
диапазоны и уровни определяются с
использованием соотношений
![]() ,
,
![]() ,
,
![]()
а среднеквадратическая
ошибка квантования будет равна
![]() .
То
есть, как и в случае дискретизации
качество квантованного изображения
зависит от шага квантования
.
То
есть, как и в случае дискретизации
качество квантованного изображения
зависит от шага квантования
![]() .
.
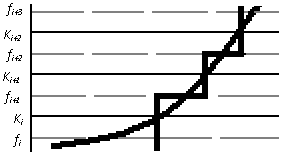 Рисунок
3 – Уровни квантования
Рисунок
3 – Уровни квантования
