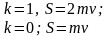- •Теоретическая механика
- •Основные понятия и аксиомы статики
- •1.1.1 Основные понятия
- •1.1.2 Аксиомы статики
- •1.3 Сложение сил на плоскости
- •1.3.1 Векторный (геометрический) способ сложения сил.
- •1.4.2 Теорема о трех непараллельных силах.
- •1.5 Вопросы для самоконтроля
- •2.1 Момент силы относительно центра (точки). Теорема Вариньона
- •2.1.1 Момент силы относительно центра.
- •2.1.2 Теорема Вариньона.
- •2.2 Теория пар сил, свойства пар сил
- •2.2.1 Основные понятия.
- •2.2.2 Свойства пар сил.
- •Приведение сил к заданному центру
- •2.3.1 Лемма Пуансо.
- •2.3.2 Теорема Пуансо.
- •2 .3.3 Частные случаи.
- •2.5 Вопросы для самоконтроля
- •3.1 Параллельные силы
- •Основная форма условий равновесия.
- •Вторая форма условий равновесия:
- •3.2 Распределенные нагрузки
- •3.3 Равновесие системы тел
- •3.4 Вопросы для самоконтроля
- •4.1 Момент силы относительно оси
- •4.2 Пространственная система сил
- •Уравнения равновесия произвольной пространственной системы сил в аналитической форме имеют вид:
- •Аналитические условия равновесия различных систем сил
- •4.4 Вопросы для самоконтроля
- •5.1 Трение
- •5.1.1 Трение скольжения
- •5.1.2 Трение качения
- •5.1.3 Трение верчения
- •5 .2 Центр тяжести твердого тела
- •5 .3 Статическая устойчивость
- •5.3.1 Устойчивость при опрокидывании
- •5.3.2 Устойчивость трактора на склоне
- •5.4 Вопросы для самоконтроля
- •Лекция №6
- •6.1 Основные понятия кинематики
- •6.2 Векторный способ задания движения точки
- •6.3 Координатный способ задания движения точки
- •Естественный способ задания движения точки
- •7.1 Поступательное движение твердого тела
- •7 .2 Вращательное движение твердого тела
- •7.3 Передаточные механизмы
- •7.4 Вопросы для самоконтроля
- •8.1 Плоское движение твердого тела
- •8.1.1 Свойства плоского движения:
- •8.1.2 Теорема сложения скоростей плоской фигуры:
- •8.1.4 Теорема о сложении ускорений плоской фигуры
- •8.2 Сложное движение точки (тела)
- •8.2.3 Сложение вращательных движений твердого тела
- •8.3 Вопросы для самоконтроля
- •Лекция №9
- •9.1 Законы динамики (Ньютона)
- •9.2 Системы единиц в механике
- •9.3 Дифференциальные уравнения движения материальной точки
- •9.3.1 Уравнения движения точки в декартовых координатах
- •9.3.2 Уравнение движения точки в естественных координатах
- •9.4 Вопросы для самоконтроля
- •10.1 Гармонические колебания точки под действием восстанавливающей силы
- •Свойства свободных гармонических колебаний:
- •А мплитуда а и начальная фаза α зависят от начальных условий;
- •Затухающие колебания точки при линейном законе сопротивления среды
- •10.3 Вопросы для самоконтроля
- •11.1 Вынужденные колебания точки в отсутствие сопротивления среды
- •11.2 Вынужденные колебания точки при вязком сопротивлении среды
- •11.3 Вопросы для самоконтроля
- •12.1 Относительное движение точки
- •12.1.1 Принципы относительности
- •Обозначим: - переносная сила инерции;
- •12.1.3 Сила тяготения, сила тяжести, вес.
- •12.2 Механическая система
- •12.2.2 Масса системы. Центр масс
- •12.2.6 Главные оси инерции
- •12.3 Вопросы для самоконтроля
- •13.1 Работа силы
- •13.1.6 Графический способ вычисления работы силы
- •1 3.1.7 Теоремы о работе силы:
- •13.1.8 Работа сил приложенных к вращающемуся телу
- •13.2 Мощность. Коэффициент полезного действия
- •13.3 Кинетическая энергия
- •Неизменяемая система
- •Система с идеальными связями
- •13.4 Вопросы для самоконтроля
- •14.1 Количество движения точки и системы. Импульс силы
- •14.2 Момент количества движения (кинетический момент)
- •14.3 Уравнение вращательного движения твердого тела
- •14.4 Уравнения плоского движения твердого тела
- •14.5 Вопросы для самоконтроля
- •15.1 Принцип Даламбера
- •15.2 Реакции, действующие на ось вращающегося тела
- •15.3 Вопросы для самоконтроля
- •16.1 Классификация связей
- •16.2 Возможные перемещения системы
- •16.3 Обобщенные координаты. Число степеней свободы системы
- •16.4 Принцип возможных перемещений
- •16.4.2 Примеры простейших механизмов:
- •16.5 Общее уравнение динамики
- •16.6 Вопросы для самоконтроля
- •17.1 Обобщенные скорости
- •17.2 Обобщенные силы
- •17.3 Уравнения Лагранжа (второго рода)
- •17.4 Вопросы для самоконтроля
- •18.1 Теория удара. Основные понятия и теоремы
- •18.1.1 Основные понятия.
- •18.2 Удар точки о неподвижную поверхность
- •1 8.2.1 Прямой удар.
- •18.2.2 Косой удар
- •18.2.3 Экспериментальное определение коэффициента восстановления.
- •18.2.4 Теоремы Карно.
- •18.3 Центральный удар двух тел
- •18.3.1 Прямой центральный удар.
- •18.4 Удар по телу, имеющему ось вращения. Центр удара
- •18.5 Вопросы для самоконтроля
17.4 Вопросы для самоконтроля
Что такое обобщенные скорости системы? В каких единицах они измеряются?
Что такое обобщенные силы? В каких единицах они измеряются? Каков порядок вычисления обобщенной силы?
Как математически записываются Уравнения Лагранжа? В чем их преимущества? Каков порядок составления?
ЛЕКЦИЯ №18
18.1 Теория удара. Основные понятия и теоремы
18.1.1 Основные понятия.
У даром
называется
явление, при котором за ничтожно малый
промежуток времени скорости точек тела
изменяются на конечную величину.
даром
называется
явление, при котором за ничтожно малый
промежуток времени скорости точек тела
изменяются на конечную величину.
Ударными силами называются силы, под действием которых происходит удар.
Временем удара называется промежуток времени, в течение которого происходит удар.
Ударный импульс равен:
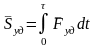 .
.
Графически
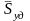 изображается
заштрихованной площадью под кривой
изображается
заштрихованной площадью под кривой
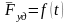 .
.
Средняя ударная сила равна:
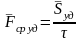 .
.
Так
как τ
мало,
то
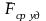 велико,
поэтому
велико,
поэтому
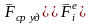 ,
а
,
а
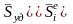 .
Поэтому импульсами неударных сил
пренебрегают.
.
Поэтому импульсами неударных сил
пренебрегают.
Так как τ мало, то считают, что за время удара точки тела не успевают изменить своего положения, поэтому перемещениями точек тел за время удара пренебрегают.
18.1.2 Основные теоремы теории удара:
Теорема об изменении количества движения точки при ударе: Изменение количества движения точки за время удара равно ударному импульсу, приложенному к точке.
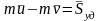 ,
,
где
и
 -
скорости точки до и после удара.
-
скорости точки до и после удара.
Теорема об изменении количества движения системы при ударе: Изменение количества движения системы за время удара равно векторной сумме внешних ударных импульсов, приложенных к точкам системы.
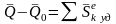 .
.
Следствие:
Если
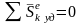 ,
то
,
то
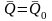 ,
то есть количество движения системы не
изменяется, если сумма внешних ударных
импульсов равна нулю.
,
то есть количество движения системы не
изменяется, если сумма внешних ударных
импульсов равна нулю.
Теорема о движении центра масс системы:
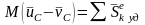 .
.
Следствие:
Если
,
то
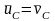 ,
то есть скорость центра масс системы
не изменится, если сумма внешних ударных
импульсов равна нулю.
,
то есть скорость центра масс системы
не изменится, если сумма внешних ударных
импульсов равна нулю.
Теорема Кельвина (для точки): Работа силы, приложенной к точке за какой-либо промежуток времени равна скалярному произведению импульса силы за тот же промежуток времени на полусумму начальной и конечной скоростей.
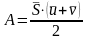 .
.
Теорема Кельвина для системы:
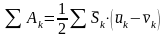 .
.
Теорема об изменении кинетического момента системы при ударе: Изменение кинетического момента системы относительно точки за время удара равно векторной сумме моментов относительно той же точки внешних ударных импульсов приложенных к точкам системы.
 .
.
В проекциях на координатные оси:
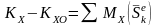 ;
;
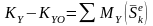 ;
;
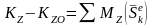 .
.
Следствия:
Если
удар испытывает твердое тело, вращающееся
вокруг оси, то, так как
;
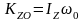 ,
,
Для
твердого тела
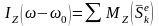 .
.
Если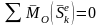 ,
то
,
то
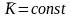 - это закон сохранения кинетического
момента при ударе.
- это закон сохранения кинетического
момента при ударе.
18.2 Удар точки о неподвижную поверхность
1 8.2.1 Прямой удар.
Удар называется прямым, если скорость точки до удара направлена по нормали к поверхности, скорость точки после удара также направлено по нормали.
Для оценки ударных свойств поверхности служит коэффициент восстановления.
Коэффициентом восстановления называется отношение модулей скоростей после и до удара:
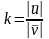 .
.
Частные случаи:
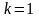 ;
;
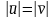 - это абсолютно
упругий удар;
- это абсолютно
упругий удар;
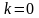 ;
;
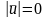 - это абсолютно
неупругий удар;
если поверхность движется, то точка
после удара движется вместе с поверхностью;
- это абсолютно
неупругий удар;
если поверхность движется, то точка
после удара движется вместе с поверхностью;
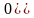 -
это частично упругий удар (упругий
удар).
-
это частично упругий удар (упругий
удар).
Процесс удара разделяется на две фазы:
1 - Фаза деформации продолжительностью τ1 от начала удара до момента максимальной деформации тела, принимаемого за материальную точку, в конце фазы скорость точки равна нулю.
2 - Фаза восстановления продолжительностью τ2 от момента максимальной деформации тела до отделения точки от поверхности.
Общее
время удара
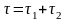 .
.
При
абсолютно упругом ударе форма
восстанавливается полностью; при упругом
- частично; при абсолютно неупругом
ударе форма не восстанавливается,
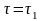 ,
- удар состоит из одной фазы.
,
- удар состоит из одной фазы.
Со стороны поверхности в первой и второй фазах на тело действует ударный импульс реакции :
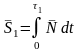 ;
;
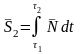 .
.
По теореме об изменении количества движения при ударе:
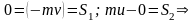
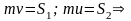
 .
.
Это выражение для коэффициента восстановления k при прямом ударе через ударные импульсы S2 и S1 за вторую и первую фазы удара. Выражение справедливо и для движущейся поверхности.
Полный ударный импульс за время удара:
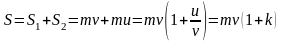 .
.
П
ударный импульс при абсолютно упругом ударе в два раза больше, чем при абсолютно неупругом
ри