15.2 Реакции, действующие на ось вращающегося тела
15.2.1 При вращении твердого тела вокруг неподвижной оси силы давления на опоры (подшипники, подпятник) переменны по величине, носят циклический характер и могут значительно превышать силы давления, которые испытывают опоры при отсутствии вращения. При вращении тела не исключена также опасность резонанса.
Например, пусть центр тяжести вала массой 10кг, вращающегося с постоянной частотой 10 000об/мин, смещен от его оси на расстояние e=1мм. Действующая на него центробежная (нормальная) сила инерции равна
;
,
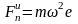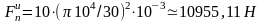что более чем в 200 раз превышает давление
в опорах от веса вала.
При ускоренном или замедленном вращения вала на опоры действуют также циклические давления от касательных составляющих сил инерции, которые также могут достигать значительных величин и стать причиной резонанса и разрушения опор.
15.2.2 Для определения реакций в опорах вращающегося тела воспользуемся принципом Даламбера.
П
усть
к телу массы М
приложены активные силы
.
Освободим тело от связей, заменив их
реакциями
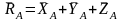и
.
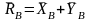Добавим к этим силам главный вектор сил
инерции
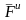и главный момент сил инерции
.
Тело находится в равновесии под действием
произвольной пространственной системы
сил. Составим шесть уравнений равновесия:
;
;
;
;
;
.
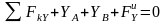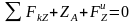Используя теорему о движении центра масс и раскладывая силы инерции, действующие на точки, на нормальные и касательные составляющие можно преобразовать эту систему уравнений равновесия [?] в следующую:
;
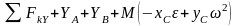=0;
=0
;
;
.
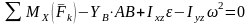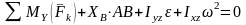Если
тело не вращается вокруг оси Z,
,
то получим уравнения статики:
;
;
;
;
;
,
из
которых можно определить статические
реакции опор
.
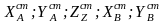Статическим
реакциями
называются части полных реакций, которые
статически уравновешивают приложенные
внешние силы
.
Уравнения для их определения получают,
положив в выражениях для полных реакций
.
Динамическими реакциями называют части полных реакций, которые уравновешивают силы инерции точек тела вращения. Уравнения для их определения получают, вычтя из выражений для полных реакций статические реакции. Динамические реакции зависят от ε и ω.
Статически
уравновешенным
называют тело, имеющее ось вращения,
если центр масс этого тела лежит на оси
вращения. В этом случае главный вектор
сил инерции равен нулю, то есть
,
а главный момент сил инерции не равен
нулю, то есть
.
Динамические реакции образуют в опорах
циклически изменяющуюся пару сил. Опоры
испытывают вибрации, которые могут
привести к их усталости и разрушению,
особенно в тех случаях, когда циклическая
частота мест крепления близка к угловой
скорости вращения тела.
Динамической
уравновешенностью
называют случай обращения в ноль
динамических реакций. В этом случае
главный вектор сил инерции равен нулю
,
а главный вектор может не равняться
нулю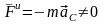
.
Полной уравновешенностью называют случай, когда полные реакции равны статическим реакциям, а центр масс тела лежит на оси вращения. В этом случае и .
15.3 Вопросы для самоконтроля
Сформулируйте принцип Даламбера для точки и системы.
В чем заключается метод кинетостатики?
Какие реакции вращающегося тела называют статическими? Как их определить?
Какие реакции вращающегося тела называют динамическими? Как их определить?
Сформулируйте условия статического уравновешивания твердого тела.
Сформулируйте условия динамического уравновешивания твердого тела.
ЛЕКЦИЯ №16