8.2.3 Сложение вращательных движений твердого тела

Вращение вокруг пересекающихся осей

П усть диск А свободно вращается вокруг оси ОО' с относительной угловой скоростью

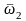. Вместе с осью ОО' диск вращается вокруг оси 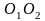с переносной угловой скоростью 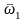. Точка О расположенная на пересечении осей ОО' и неподвижна, т.е. . Можно показать, что любая другая точка М, лежащая на диагонали параллелограмма, построенного на векторах угловых скоростей и , т.е. 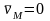. Следовательно, ось ОО" является мгновенной осью вращения диска А с абсолютной угловой скоростью .

Вращение вокруг параллельных осей

Рассмотрим три случая:

1- Вращения имеют одинаковые направления

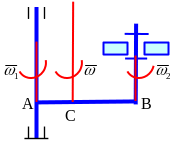
- относительная угловая скорость;

- переносная угловая скорость.

Существует ось параллельная осям вращения, скорости точек которой в данный момент равны нулю, – это мгновенная ось вращения диска, вокруг которой он вращается с угловой скоростью

;

; .

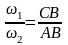Мгновенная ось вращения проходит через точку С и делит расстояние AB между осями относительного и переносного вращении внутренним образом на части обратно пропорциональные их угловым скоростям.

Тело, участвующее в двух параллельных вращениях, совершает плоское движение.

П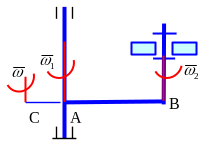 ример. Планетарный зубчатый механизм с внешним зацеплением состоит из неподвижного колеса 1 («солнечное колесо»), водила Н и сателлита 2, находящегося во внешнем зацеплении с колесом 1. Точка Р. – полюс зацепления колес 1 и 2, через который проходит мгновенная ось вращения сателлита 2, который совершает относительное вращение с угловой скоростью ω₂ вокруг оси, проходящей через точку. В водила. Водило Н совершает переносное вращение с угловой скоростью вращения вокруг оси, проходящей через точку А (центр колеса 1). Угловая скорость абсолютного вращения сателлита 2 равна

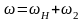, ее направление совпадает с ω₂ и с ω_Н.

2- Вращения имеют противоположные направления

Если , то

;

.

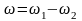И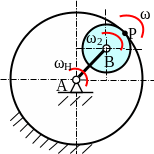 меем абсолютное вращение с угловой скоростью ω вокруг мгновенной оси, проходящей через точку С, делящую расстояние между

и (точками А и В) в обратном отношении внешним образом.

Пример. Планетарный механизм с внутренним зацеплением зубчатых колес состоит из коронного неподвижного колеса 1, водила Н и сателлита 2. Пусть , тогда

; .

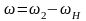Ось абсолютного вращения сателлита 2 проходит через полюс зацепления Р.

3- Пара вращений

П арой вращений называется совокупность двух вращений твердого тела переносного и относительного вокруг параллельных осей с равными по модулю и противоположно направленными угловыми скоростями. В этом случае

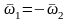; . Скорости всех точек тела одинаковы, то есть тело совершает мгновенно поступательное движение. Если тело длительно участвует в паре вращения, то скорости всех его точек равны и тело движется поступательно со скоростью (пара вращения аналогична паре сил).

Примеры участия тела в паре вращения. Кабинки колеса обозрения, ручка мясорубки, педаль велосипеда, планки мотовила зерноуборочного комбайна и т.д.

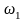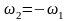На рисунке изображен механизм, состоящий из неподвижного шкива 1 и подвижного шкива 2, приводящегося в движение водилом АВ – это переносное вращение с угловой скоростью . Шкивы связаны ремнем, поэтому шкив 2 вращается с угловой скоростью , Все точки шкива 2 имеют одинаковые скорости равные , поэтому прямая MN остается параллельной своему первоначальному положению и установленный на ней стакан с жидкостью не разливается.