7.1 Поступательное движение твердого тела
К простейшим видам движения твердого тела относятся поступательное и вращательное движение.
Поступательным называется такое движение твердого тела, при котором любая прямая, жестко соединенная с телом, остается параллельной своему первоначальному положению.
Для того, чтобы убедиться, что при движении тела любая прямая остается параллельна своему первоначальному положению недостаточно провести одной прямой (например, эта прямая может оказаться осью вращения тела), поэтому надо провести две скрещивающиеся прямые.
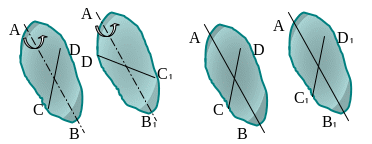
Тело вращается вокруг оси АВ перемещающейся в пространстве параллельно первоначальному положению |
Тело движется поступательно, так как скрещивающиеся прямые АВ и CD остаются параллельны первоначальному положению |
П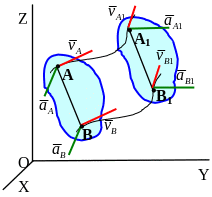
римеры
тел, совершающих поступательное движение:
педаль велосипеда, кабина «колеса
обозрения», планки мотовила зерноуборочного
комбайна, сошники пропашных веялок и
т.д.
Т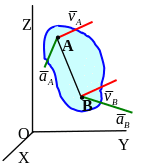
еорема
о свойствах поступательного движения:
При поступательном движении твердого
тела его точки описывают одинаковые
траектории
и имеют в каждый момент времени одинаковые
по модулю и направлению скорости и
ускорения.
Поэтому для описания движения тела,
совершающего поступательное движение,
достаточно описать движение (определить
кинематические характеристики) любой
его точки.
Мгновенно поступательным движением твердого тела называется такое его движение, при котором в данный момент времени скорости его точек равны по величине и направлению, а ускорения не равны.
7 .2 Вращательное движение твердого тела
Вращательным движением твердого тела называется такое движение твердого тела, при котором какие-нибудь две точки, принадлежащие телу, остаются все время неподвижными. Прямая, проходящая через эти точки, называется осью вращения.
При вращательном движении положение тела определяется значением угла поворота тела j, который измеряют от неподвижной плоскости П0, проведенной через ось вращения, до подвижной плоскости П, также проходящей через ось вращения и жестко связанной с вращающимся телом. Закон вращательного движения:
j = f(t).
Основными кинематическими характеристиками вращательного движения являются угловая скорость и угловое ускорение.
Угловой скоростью тела в какой либо момент времени называют первую производную от угла поворота по времени.
.
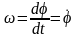В
технике угловая скорость выражается в
оборотах в минуту и называется частотой
вращения n,
=1об/мин.
За один оборот тело поворачивается на
угол равный 2π
рад, за n
оборотов на 2πn
радиан. Разделим это выражение на число
секунд в минуте:
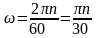рад/с.
Угловым ускорением тела в какой либо момент времени называют первую производную от его угловой скорости или второй производной от угла поворота по времени
.
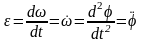В
общем случае угловая скорость и угловое
ускорение величины
векторные,
направленные вдоль оси вращения. Вектор
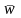направлен
в ту сторону, откуда вращение видно
происходящим против хода часовой
стрелки. Вектор
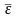направлен
по оси вращение в сторону, откуда он
«вращает» тело против хода часовой
стрелки.
В случае ускоренного вращения векторы и совпадают по направлению, в случае замедленного - направлены в противоположные стороны.
При рассмотрении вращения одного тела или вращения тел вокруг параллельных осей часто считают ω и ε величинами алгебраическими, указывая их направления дуговыми стрелками: против хода часовой стрелки «+», по ходу часовой стрелки «–».
Частные случаи вращения:
При равномерном вращении угловая скорость постоянна, а угловое ускорение равно нулю
При
.
При равнопеременном вращении (равноускоренном или равнозамедленном) угловое ускорение постоянно
.
При
Угловая скорость при равнопеременном движении равна:
.
.
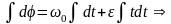
При
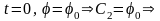
Закон движения при равнопеременном вращении имеет вид:
.
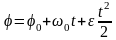В сечении тела вращения плоскостью перпендикулярной оси вращения видно, что при повороте тела на угол φ
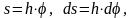
где s – дуга окружности, по которой перемещается точка К,
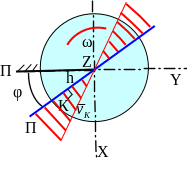h
- расстояние от точки К
до оси вращения Z.
Скорость точки К равна
.
Направлен
вектор скорости
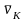перпендикулярно радиусу в сторону
вращения (по направлению
).
При увеличении расстояния от оси вращения скорость точки увеличивается по линейному закону, поэтому концы векторов скоростей, проведенных из точек, лежащих на радиусе окружности, располагаются на одной прямой, проходящей через ось вращения Z. Картина (план) скоростей точек тела вращения в плоскости перпендикулярной оси вращение имеет вид треугольников.
У
скорение
точки
тела, совершающего вращательное движение,
раскладывается на
касательное и нормальное ускорение.
Касательное ускорение
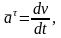но
,
Вектор направлен по касательной к описываемой точкой окружности (перпендикулярно радиусу) в сторону «указанную» угловым ускорением ε.
Нормальное ускорение
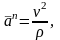так
как
,
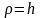, то
Нормальное
ускорение
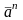всегда направлено к оси вращения.
Полное ускорение
;
.
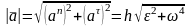
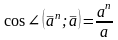