Шпоры по сопромату / Формулы

Нормальное напряжение: ; относительная деформация ; Закон Гука: ;  = Е; ; абсолют. удлинение ; относит. поперечная деформация ; коэфф.Пуассона ; удлинение стержня ; работа при растяжении ; потенциальная энергия ; учет собств. веса стержня: N(z) = P + FL; ; ; условие прочности при растяж.-сж: _max []; – допуск. напр.; линейное напряженное состояние: полное напр.: ; нормальное: ; касательное:

; на перпендикулярных площадках ; ;

_ = — _; главные напряжения: ₁>₂>₃; на наклонной площадке: ; или ; закон парности касательных напр. _xz= — _zx; ; ; ; ; ; _+_=₁+₂; макс. касательное напряжение ; главные напр-ния ;

положение главных площадок ; ;

объемное напряженное состояние: ;

;макс.касат.напр.;

напряжения по октаэдрической площадке ;

; ;

интенсивность напряжений ;

первый инвариант: _x+_y+_z=₁+₂+₃; обобщенный закон Гука:

;

относит. объемная деформация ; ;

среднее напряжение ; ; модуль объемной деформации: К=; потенц.энергия U=; удельная потенциальная энергия

u = ; ; ;

; u = u_о + u_ф; энергия из-за изменения объема: ; энергия из-за изменения формы:

; тензор напряжений:

; тензор для главных напряжений:

Инварианты напряженного состояния:

J₁= _x + _y + _z; J₂= _x_y +_y_z + _y_z — ²_xy — ²_zx — ²_yz;

J₃= _x_y_z — _x²_yz — _y²_zx — _z²_xy + 2_xy_zx_yz.

Сопоставление зависимостей напряженного и деформированного плоского сост.:

; ;

; ; Инварианты деформированного состояния:

J₁= _x + _y + _z; J₂= _x_y +_y_z + _z_x — ²_xy — ²_yz — ²_zx;

тензор деформаций:; .

1-ая теория прочности (теория наибольших нормальных напряжений):_max= ₁ [].

2-ая теор. прочности (теория наибольших относительных деформаций): _max= ₁ []. ₁=, условие прочности _эквII= ₁ — (₂ + ₃) [].

3-я теор. проч. (теория наибольших касательных напряжений):_max  [], _max=,

условие прочности: _эквIII= ₁ — ₃ [], _эквIII=  []. При _y=0 . 4-я теор. прочности (энергетическая теория):

u_ф[u_ф]. . Для плоского напряж. сост.: . _y=0,  .

Теория прочности Мора:, когда допускаемые напряжения на растяжение [_p] и сжатие [_с] не одинаковы (чугун).

Чистый сдвиг. ; угол сдвига   . Закон Гука при сдвиге:  = /G;  = G;

модуль сдвига (модуль второго рода): ; потенциальная энергия при сдвиге ; удельная потенц. энергия: ; объем V=аF; ;

Геометрические характеристики сечений: площадь ; статический момент относительно оси x или y: ; ; координаты центра тяжести:

; ; ;

Осевой момент инерции: ; ; полярный момент инер.: ;

J_y + J_x = J_p; центробежный момент инерции: . Прямоугольник:

; J_xy=0. Круг: . Четверть круга: J_y=J_x=0,055R⁴; J_xy=0,0165R⁴; J_x0=0,0714R⁴; J_y0=0,0384R⁴. Моменты инерции относительно параллельных осей: J_x1=J_x + a²F; J_y1=J_y + b²F; J_y1x1=J_yx + abF. Моменты инерции при повороте осей: J_x1=J_xcos² + J_ysin² — J_xysin2; J_y1=J_ycos² + J_xsin² + J_xysin2; J_x1y1=(J_x — J_y)sin2 + J_xycos2; J_y1 + J_x1= J_y + J_x. Угол, определяющий положение главных осей: . Мом-ты инерц. относит. главн. центр. осей инерц.: ; J_max+J_min=J_x+J_y.

Радиус инерции: ; J_x=Fi_x², J_y=Fi_y². Осевой момент сопротивления:

; для прямоугольника: ; для круга:

W_x=W_y= ; трубчатое сечение (кольцо): W_x=W_y= ;

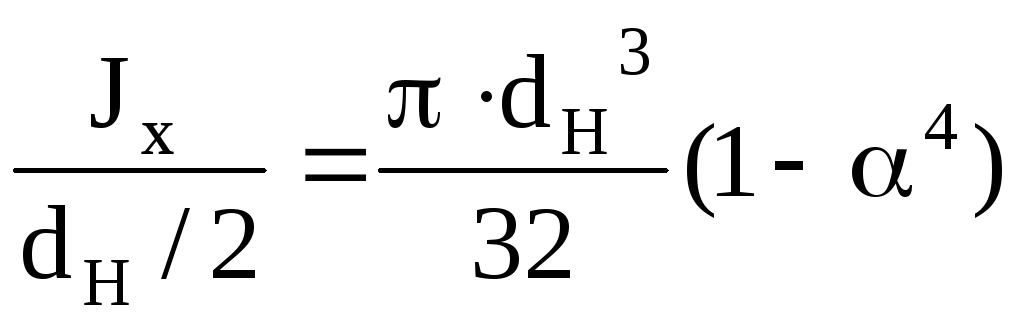 = d_Н/d_B. Полярный момент сопротивления: ; для круга:W_р= .

Кручение. , . Угол закручивания: ; относит. угол закручивания: . Потенциальная энергия при кручении: ;

Условие прочности: ; [] =; условие жесткости: _mкax[]. Кручение бруса прямоугольного сеч.: ; ; W_k= hb²; J_k= hb³; = _max.

Изгиб. . Нормальные напряжения: . Закон Гука при изгибе: , формула Навье: . Максимальные напряжения:

, J_x/y_max=W_x—момент сопротивления сечения при изгибе, .

Касательные напряжения – формула Журавского: . Для прямоугольного сечения: , F=bh, для круглого сечения:, F=R², для любого сечения: . Главные напряжения при поперечном изгибе: .

Условие прочности по нормальным напряжениям , условие прочности по касательным напряжениям .

Условия прочности по различным теориям прочн.: I-я: ;

II-я: (при коэфф.Пуассона =0,3);

III-я:, IV-я:,

теория Мора: , .

Закон Гука при изгибе: . — дифференциальное уравнение изогнутой оси балки. Приближенное дифференциальное уравнение изогнутой оси балки: . — уравнение углов поворота, — уравнение прогибов. Метод начальных параметров.

EJ= M(x) = R_Ax – – M(x – a)⁰ + – P(x – a – b); интегрируем:

EJ = EJ₀ + R_A – – M(x – a) + – P;

EJy =EJy₀ + EJ₀x + R_A – – M + – P.

Дифференциальные зависимости при изгибе: ; ;

; . Определение перемещений способом фиктивной нагрузки.

; ; ; ; . Теорема о трех моментах:

.

Косой изгиб. Напряжение в произв. точке с координатами "x,y": ;

, M_x=Mcos; M_y=Msin, . Уравнение нейтр. линии:

, или .Угол наклона нейтральной линии к главной оси "х": . . Наиб. напр. ,

W_x=J_x/y_max; W_y=J_y/x_max. Прогиб "f": , .

Внецентренное сжатие–растяжение. Нормальное напряжение в произвольной точке:

; N>0 – если сила растягивающая, M_x, M_y>0, если моменты "растягивают" сеч. в I-ой четверти. Внутренние усилия: N=P; M_y=Px_p; M_x=Py_p. Напряжения: или ,

Уравнение нейтр. линии: . Отрезки, отсекаемые нейтр. линией на осях коорд.: . – координаты контура ядра.

Изгиб с кручением. Макс. нормальные и касательные напряжения в опасных точках:

, , (для круга: W=–осевой момент сопротивления, W_р= –полярный момент сопротивления сечения). Главные напряжения в опасных точках:

Проверка прочности: по IV-ой теории прочности:

теория Мора: m=[_p]/[_c].

.

Приведенный момент: ;

I-ая теория:

II-ая: , при коэффициент Пуассона =0,3;

III-я: IV-ая: ;

, момент сопротивления: , диаметр вала: .

Перемещение, вызванное несколькими силовыми факторами: _Р=_РP+_РQ+_РM. Перемещение вызванное силой Р, будет: _Р=Р_Р. Работа внешних сил, действующих на упругую систему: . – работа при статическом действии обобщенной силы на упругую систему.

Работа внутренних сил (сил упругости) в случае плоского изгиба: . Потенциальная энергия U=A.

Теорема о взаимности работ (теорема Бетли): А₁₂=А₂₁, Р₁₁₂=Р₂₂₁.

₁₁– перемещение по направлению силы Р₁ от действия силы Р₁;

₁₂– перемещение по направлению силы Р₁ от действия силы Р₂;

₂₁– перемещение по направлению силы Р₂ от действия силы Р₁;

₂₂– перемещение по направлению силы Р₂ от действия силы Р₂.

А₁₂=Р₁₁₂ – работа силы Р₁ первого состояния на перемещении по ее направлению, вызванном силой Р₂ второго состояния. Аналогично: А₂₁=Р₂₂₁ – работа силы Р₂ второго состояния на перемещении по ее направлению, вызванном силой Р₁ первого состояния..

Т

еорема о взаимности перемещений (теорема Максвелла) Если Р₁=1 и Р₂=1, то Р₁₁₂=Р₂₂₁, т.е. ₁₂=₂₁, в общем случае _mn=_nm. Обобщенное перемещение (формула или интеграл Мора):

Для плоской системы: . .

Вычисление интегр. Мора способом Верещагина. . .

Перемножение эпюр, имеющих вид трапеций: .

П

₁₁Х₁+₁₂Х₂+…+_1nХ_n+_1p=0

₂₁Х₁+₂₂Х₂+…+_2nХ_n+_2p=0

. . . . . . . . . . . .

_n1Х₁+_n2Х₂+…+_nnХ_n+_np=0

ри действии равномерно распределенной нагрузки на шарнирно опертую балку эпюра строится в виде выпуклой квадратичной параболы, площадь , , т.е. , х_С=L/2. Для "глухой" заделки при равномерно распределенной нагрузке имеем вогнутую квадратичную параболу, для которой ; , , х_С=3L/4. Теорема Кастильяно: , , .

Канонические уравнения метода сил:

; ; ….; ;

; ; ….; ;

; ; ….; ,

коэффициенты находят по способу Верещагина: ; и т.д.

При чистом изгибе кривых брусьев большой кривизны: ; –

радиус нейтр. слоя Для прямоугольного сеч. высотой h, с наружным радиусом R₂ и внутренним R₁: . При h/R<1/2 . При наличии N: .

Условие прочности: , y= – h₂ или y= h₁.

Продольный изгиб. Устойчивость. Формула Эйлера: – для стержня с шарнирно закрепленными концами. При различных закреплениях: ,

 – коэффициент приведения длины. При шарнирном закреплении обоих концов стержня  = 1; для стержня с заделанными концами  = 0,5; для стержня с одним заделанным и другим свободным концом  = 2; для стержня с одним заделанным и другим шарнирно закрепленным концом  = 0,7.

Критическое сжимающее напряжение.: , – гибкость стержня, – наименьший главный радиус инерции. Формула Эйлера применима при гибкости стержня: . Для ₀<  < _кр используется формула Ясинского: _кр= a — b, где ₀, при котором _кр=_т, a,b – опытные данные, для стали Ст3:

40 <  < 100.

Условие устойчивости: ; [_у]=_кр/n_у; [_у]=[]. – площадь брутто поперечного сечения, т.е. без учета его ослаблений.