Т е м п е р а т у р н ы е н а п р я ж е н и я

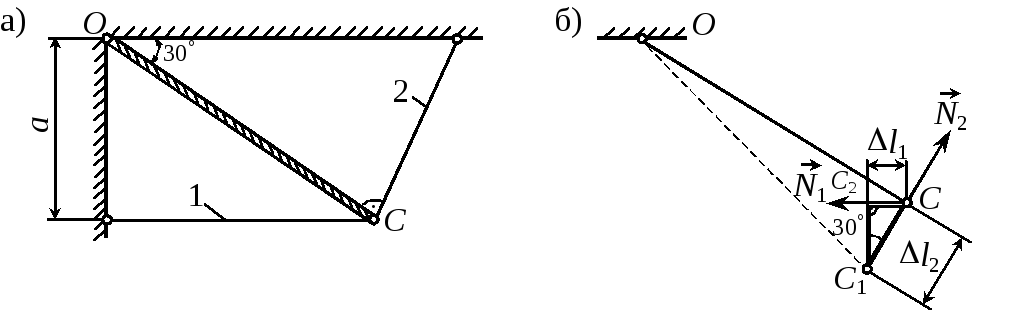
П р и м е р 2.10. Определить напряжения, возникающие в упругих элементах системы (рис. 2.18), если после монтажа температура увеличилась на t = 40C. Дано: А₁/А₂ = 2, Е = 200 ГПа,  = 12510^-7.

Рис. 2.18

Р е ш е н и е

Данная система является однажды статически неопределимой.

Уравнение статики m_Q = 0, N₂OC-N₁OCsin30 = 0,

N₂ = N₁sin30 или ₂А = ₁2Аsin30, откуда ₁ = ₂. (1)

Уравнение совместности деформаций l₁ = -l₂sin30

или .

Переходя от усилий к напряжениям, получим

₁l₁ + ₂l₂sin30 = -Et(l₁ + l₂sin30). (2)

Решая совместно (1) и (2), найдем температурные напряжения

₁ = ₂ = -Et = -12510^-720010⁹40 = -100 МПа.

2.2.3. Расчет по допускаемым нагрузкам

Метод расчета по допускаемым нагрузкам исходит из более широкого использования экспериментальных данных, анализа пластических свойств материалов и их учета.

В этом методе путем расчета определяются не напряжения, а находится предельная нагрузка F_пред, при которой конструкция становится непригодной для эксплуатации. За допускаемую нагрузку принимается доля от предельной [F_F] = F_пред/П и условие прочности в данном случае принимает вид

F_max  [F_F]. (2.12)

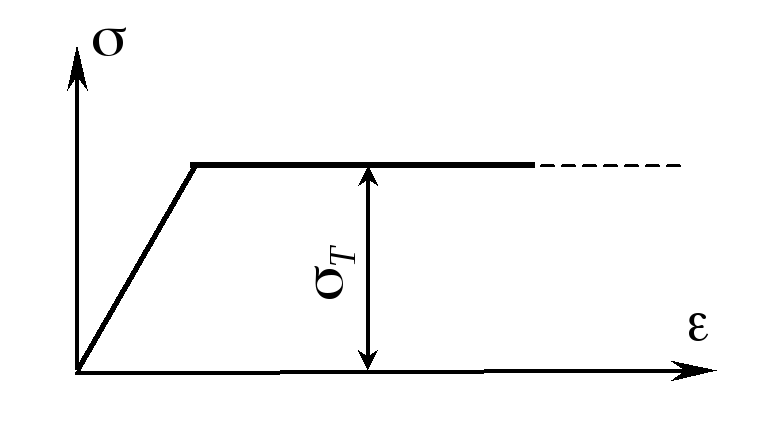
При определении предельной нагрузки действительную диаграмму растяжения материала заменяют идеализированной диаграммой Прандтля, в которой площадка текучести принимается неограниченной (рис. 2.19). Поэтому расчет по допускаемым нагрузкам применим лишь для конструкций, выполненных из пластичных материалов и только при действии статических нагрузок.

Теоретическое определение допускаемой нагрузки возможно только для некоторых простейших случаев. Один из подходов состоит в том, что рассматриваются различные кинематически возможные схемы исчерпания несущей способности системы (система становится геометрически изменяемой). Продольные усилия в элементах, появление

текучести в которых приводит к исчерпанию несущей способности конструкции, принимаются равными произведениям допускаемых напряжений на площади попе-

Рис. 2.19

речных сечений. Из уравнений предельного равновесия определяются допускаемые нагрузки, соответствующие каждому из вариантов исчерпания несущей способности. В качестве допускаемой нагрузки для конструкции принимается наименьшая из найденных величин.

П р и м е р 2.11 Определить величину допускаемой нагрузки для данной конструкции, если А1 = =А2 = А3 = А, l1 = l2 = l3 = l. Все стержни изготовлены из одного и того же материала.

Рис. 2.20

Р е ш е н и е. Данная система является один раз статически неопределимой (три неизвестных при двух независимых уравнениях статики). Несущая способность ее будет исчерпана (система станет геометрически изменяемой), когда возникнут пластические деформации в двух стержнях. Таких вариантов три.

Первый вариант (рис. 2.20,б). Несущая способность исчерпывается при появлении пластических деформаций в 1-м и 2-м стержнях. Принимаем N₁ = N₂ = []A и составляем уравнение моментов относительно точки С m_C = 0,

, откуда .

В т о р о й в а р и а н т (рис. 2.20,в). Несущая способность исчерпывается при появлении пластических деформаций в 1 и 3-м стержнях. Принимаем N₁ = N₃ = []A и составляем уравнение моментов относительно точки В: m_В = 0,

, откуда .

Т р е т и й в а р и а н т (рис. 2.20,г). Несущая способность исчерпывается при появлении пластических деформаций во 2 и 3-м стержнях. Принимаем N₁ = N₂ = []A и составляем уравнение моментов относительно точки А: m_А = 0,

, откуда .

Допускаемой нагрузкой для конструкции будет наименьшая из трех найденных величин:

.

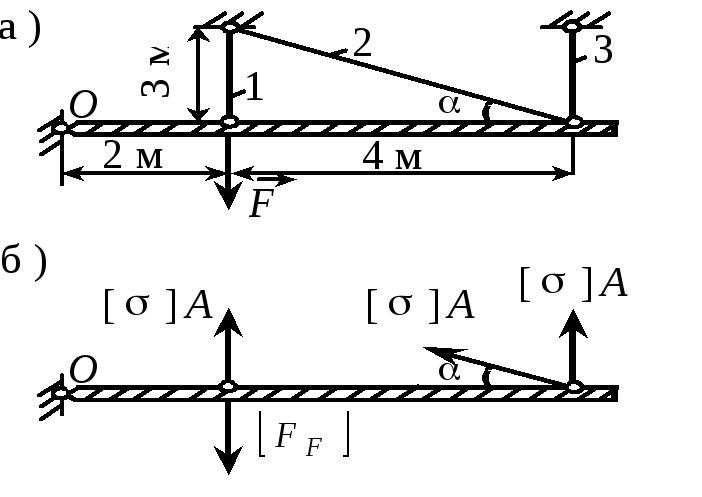
П р и м е р 2.12 Подобрать сечения стержней, если А1 = А2 = А3 = А, F = 870 кН, допускаемое напряжение  = 150 МПа. Р е ш е н и е 1. Определение допускаемой нагрузки. Несущая способность конструкции будет исчерпана, когда

Рис. 2.21

пластические деформации возникнут во всех трех стержнях. Полагая N₁ = N₂ = N₃ = А и составляя уравнение моментов относительно точки О, найдем допускаемую нагрузку

m_О = 0,

,

откуда .

2. Подбор сечений. Записываем условие прочности

,

откуда находим искомую площадь

.

С О Д Е Р Ж А Н И Е

1. ЭПЮРЫ ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ …...	4
1.1. О б щ и е с в е д е н и я …………………………...	4
1.2. Построение эпюр для стержней, нагруженных осевыми силами………………………………….…	5
1.3. Построение эпюр для стержней, нагруженных скручивающими парами …………………………..	10
1.4. Построение эпюр для балок и рам ………………	12
2. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОЛИНЕЙНОГО СТЕРЖНЯ …………………………..	29
2.1. Статически определимые системы ……………….	29
2.2. Статически неопределимые системы …………….	40
2.2.1. О б щ и е с в е д е н и я …………………….	40
2.2.2. Расчет по допускаемым напряжениям …….	42
2.2.3. Расчет по допускаемым нагрузкам ………...	48

52