12.3. Полиномиальная лаговая структура Ширли Алмон

Подход основан на полиномиальной форме параметризации конечной лаговой структуры ₀, ₁,..., _T. А именно, опираясь на теорему Вейер-штрасса (которая утверждает, что непрерывная на замкнутом интервале функция может быть приближена на всем отрезке многочленом подходящей степени от ее аргумента, отличающимся от этой функции в любой точке меньше, чем на любое заданное число) и рассматривая весовые коэффициенты _k как функции k, автор предложила выразить их в виде полиномов невысокой степени m (m ≤ 3) от k, т. е.

_k = ₀ + ₁k + ₂k² + ... + _mk^m, k = 0,1,2,... ,Т, (12.3)

где ₀, ₁,..., _m – некоторые неизвестные параметры, которые определяются из условия наиболее точной (в определенном смысле) подгонке модели (12.2).

Подставлял последовательно в (4) k= 0,1,2,..., T, получаем:

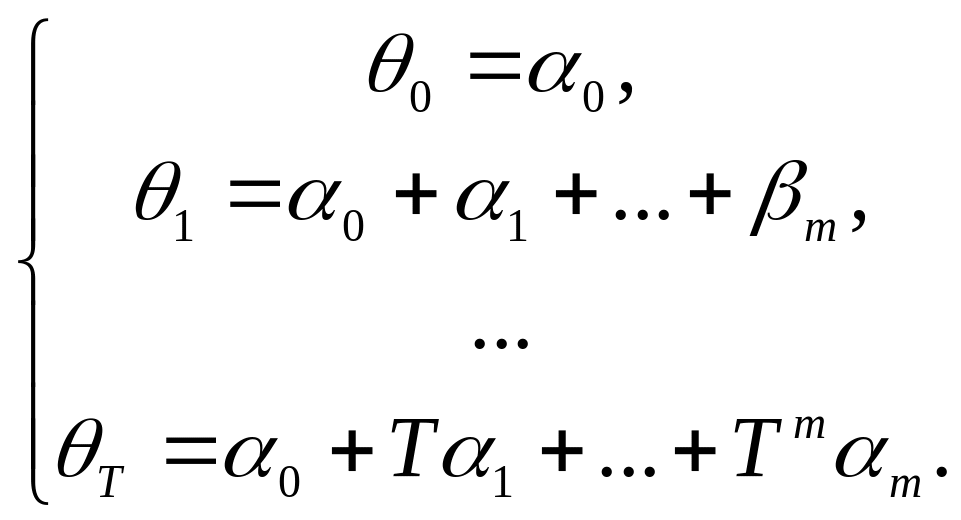
Возвращаемся к анализируемой модели (12.2) заменяя в ней коэффициенты их выражениями по формулам (12.3) суть метода Алмон:

y(t) = c₀ + x(t-k) + (t) = c₀

+ ₀x(t)

+ ₀x(t-1) + ₁x(t-1) + …+ _mx(t-1)

+ ₀x(t-2) + 2 ₁x(t-2) + …+2^m _mx(t-1)

…………………………………………………..

+ ₀x(t-T) + T ₁x(t_T) + …+2^m _mx(t-T) + (t) (12. 4)

Суммируя с_о и остальные слагаемые правой части (12.4) по столбцам, получаем:

y(t) = c₀ + ₀[x(t)+ x(t-1)+ … + x(t-T)]

+ ₁[x(t-1)+ 2x(t-2)+ … + Tx(t-T)]

…………………………………………

+ _m[x(t-1)+ 2^mx(t-2)+ … + T^mx(t-T)]

+ (t) (12.5)

Обозначая первую квадратную скобку в правой части (12.5) как вторую – как ,..., m-ю – как , где «новое» время t' «привязано» к моменту времени (t – Т) (т. e. t' = t – Т), получаем:

y(t’+T) = c₀ + ₀x⁽¹⁾(t’) + ₁x⁽²⁾(t’) + …+ _mx^(m)(t’) + (t+T) (12.5')

В результате мы свели задачу оценивания (T + 2) неизвестных весовых коэффициентов с_о, ₀, ₁,…, _T к статистическому анализу стандартной линейной модели множественной регрессии всего с т + 1 (m ≤ 3) неизвестными параметрами (при этом предполагается, конечно, что длина исходных временных рядов N много больше, чем Т + т). Так что оценки с_о и _j– параметров с_о и _j (j = 1,2,…,m) получаются с помощью обычного МНК, после чего по формулам (12.5') вычисляются оценки _k (k = 0,1,..., Т).

Заметим, что мы полагали в данной схеме максимальную величину лага Т известной. В действительности она, как правило, определяется статистически. Обычно проводят описанные выше расчеты для нескольких предположительных значений Т и окончательный выбор между ними производят на основании диагностики полученных моделей, т. е. – путем сравнения различных характеристик их точности.

Преимущества метода Алмон. Он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов.

При относительно небольшом числе переменных в модели не приводящем к значительной потере числа степеней свободы, с помощью метода Алмон можно построить модели с распределенным лагом любой длины (максимальный лаг L может быть достаточно большим).

12.4. Геометрическая лаговая структура Койка

В данном подходе рассматривается бесконечном лаговая структура (т.е. полагается Т → ∞), поэтому он применим лишь к достаточно длинным временным рядам (12.1). Общим (и естественным!) допущением при анализе бесконечных лаговых структур является требование сходимости ряда. Это означает, что влияние x{t) на y(t + к) уменьшается до нуля по мере неограниченного увеличения временного интервала k, что естественно, т.к. текущее значение y практически не должно зависеть от поведения х в бесконечно далеком прошлом. Койк в своем подходе конкретизировал и усилил это допущение. В частности, он постулировал, что все нормированные веса , являясь положительными, убывают с ростом k по геометрической прогрессии, т. е.

w_k = (1– ) ^k , где 0 1 (12.6)

(множитель (1 – ) в соотношении (12.6) нужен для того, чтобы обеспечить условие нормировки w_k = 1).

Как видно, это допущение приводит к огромным упрощениям модели (12.2), т.к. вместо оценивания бесконечного ряда весовых коэффициентов ₀, ₁, ₂ ,… придется оценить лишь два параметра: и = _k.

Возвращаясь к (12.2), имеем:

y(t) = c₀ + _kx(t-k)+ (t) =с_.0+ (1– ) ^k x(t-k)+ (t)= c₀+ (1– )( ^k F_ ^k) x(t)+ (t) (12.7)

где F_, оператор сдвига назад на единицу, т.е. F-x(t) = x(t – 1). Произведя формальные операции с операторами сдвига, получаем

(1- F_)y(t)=(1- F_)c₀+ (1- )x(t)+(1- F_) (t), (12.8)

Финальный вид (12.8') модели Койка может быть получен и без помощи операций с оператором сдвига F_. Для этого выпишем исходный вид модели для двух текущих моментов времени t и (t-1):

y(t) = c₀ + (1 - ) ^k x(t-k) + (t) (12.9)

y(t-1) = c₀+ (1 - ) ^kx(t-1-k) + (t-1).

Умножив второе уравнение на и вычтя полученный результат из первого уравнения, приходим к (12.8).