6.3. Тест Глейзера

Тест проводится в несколько этапов.

1. Предположим, что на основе выборочных данных была построена линейная модель множественной регрессии:

где y_i – результативная переменная, i=1,2,….n;

x_mi– факторные переменные ( m – 1,2,3; i=1,2,…,n);

– неизвестные коэффициенты модели регрессии;

– случайная ошибка модели регрессии.

2. Оценки неизвестных коэффициентов модели множественной регрессии проводятся методом наименьших квадратов:

3. Далее рассчитывается оценка случайной ошибки модели регрессии 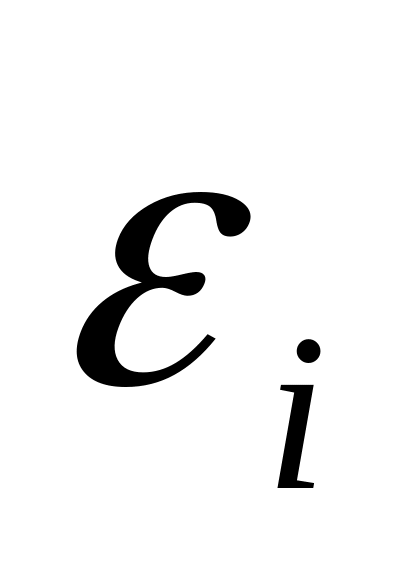, т.е. вычисляются остатки случайной модели множественной регрессии:

4. Полученные остатки линейной модели множественной регрессии возводят в квадрат ().

5. Рассчитывается коэффициент Спирмена между квадратом остатков модели множественной регрессии 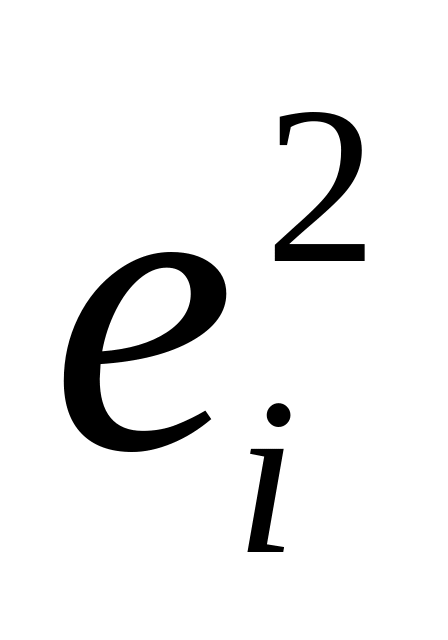и факторными переменными x_mi (m = 1,2,3; i = 1,2,…,n).

6.4. Тестовые задания для самостоятельной работы

1. Явление гетероскедастичности свидетельствует о том, что:

1) отсутствует систематическая связь между значениями случайного члена в любых двух наблюдениях;

2) дисперсия каждого отклонения одинаковы для всех значений х;

3) математическое ожидание случайного члена в любом наблюдении должно быть равно 0.

2. На каком из графиков поля корреляции изображено явление гетероскедастичности.

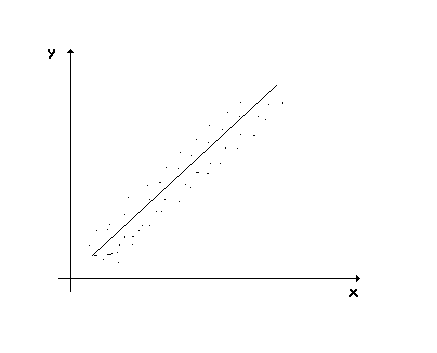
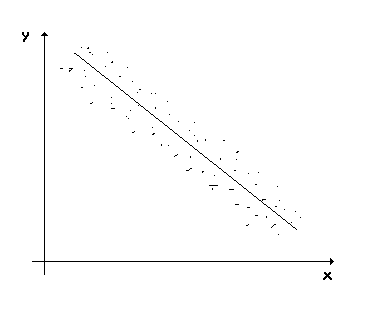
а 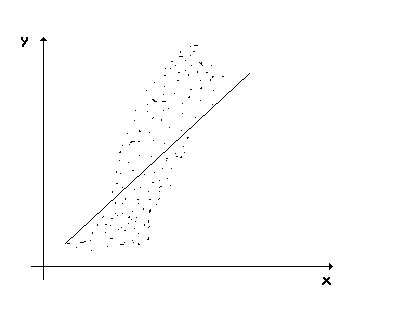) б) в)

3. Метод наименьших квадратов эффективен, когда имеет место:

1) гетероскедастичность;

2) автокоррелляция остатков;

3) гомоскедастичность.

4. Тесты на гетероскедастичность используют в качестве нулевой гипотезу H₀:

1) гипотеза о случайной природе оцениваемых характеристик;

2) гипотеза об отсутствии гетероскедастичности;

3) гипотеза об отсутствии гомоскедастичности.

5. Чтобы установить наличие гомо– или гетероскедастичности проводят:

1) тест Чоу;

2) тест Голдфелда-Квандта;

3) тест Дарбина-Уотсона.

6. Пусть сумма квадратов разностей между рангами значений регрессоров x_i и остатков e_i равна 86,345 ,т.е. . Количество наблюдений , уровень значимости , число степеней свободы . С помощью теста ранговой корреляции Спирмена определить, будет ли принята гипотеза H₀:

1) гипотеза принимается;

2) гипотеза отвергается.

7. По данным наблюдений выяснить, можно ли считать на уровне значимости линейную регрессионную модель Y по x₁ и x₂ гетероскедастичной. число степеней свободы , где p – число регрессоров:

1) гипотеза принимается;

2) гипотеза отвергается.

8. С помощью теста Уайта выявить можно ли считать на уровне значимости 0,01 линейную регрессионную модель y по x гетероскедастичной . . Проверку проводить по критерию Пирсона .

1) гипотеза принимается;

2) гипотеза отвергается.

9. Пусть сумма квадратов разностей между рангами значений регрессоров x_i и остатков e_i равна 35,472, т.е.

. Количество наблюдений n=11 уровень значимости число степеней свободы . С помощью теста Спирмена определить, имеет ли место гетероскедастичность:

1) , гипотеза отвергается;

2) , гипотеза отвергается;

3) , гипотеза отвергается.

10. По данным наблюдений выяснить, можно ли считать на уровне значимости линейную регрессию y по x гетероскедастичной

;

1) F = 0,4498, гипотеза принимается;

2) F = 2,6234, гипотеза отвергается;

3) F = 2,2234, гипотеза принимается.