3.3. Ячеечная модель аппарата

Ячеечную модель применяют для описания структуры потоков в аппаратах, потоки в которых не могут быть описаны моделями полного смешения или полного вытеснения. В этом случае предполагают, что весь объем аппарат может быть разделен на элементарные объемы, каждый из которых описывается моделью полного смешения. Такая модель применима также для описания потоков в каскаде последовательно соединенных аппаратов смешения. Рассмотрим движение смеси в таком каскаде аппаратов.

Рис.3.3.1 Схема ячеечной модели аппарата

v- объемный расход вещества, V_i объем ячейки (i=1,…,n) n – число ячеек,

c_i – концентрация вещества в i-м аппарате.

Составим математическое описание, описывающее структуру потоков в ячеечной модели.

Учитывая, что каждая ячейка представляет собой аппарат идеального смешения, для первой ячейки можно записать:

Продолжая эту операцию последовательно до последнего аппарата каскада, получим для выходной концентрации из каскада следующее выражение:

(3.3.1)

Отсюда получаем выражение для передаточной функции ячеечной модели:

(3.3.2)

Передаточная функция n последовательно соединенных ячеек полного смешения равна произведению передаточных функций отдельных ячеек.

При условии, что V₁= V₂= V_i= V_n и v=const передаточные функции отдельных ячеек будут равны и передаточная функция, будет иметь вид:

(3.3.3)

Где - среднее время пребывания смеси во всем аппарате, - среднее время пребывания в одной ячейке.

Рис.3.3.2. Кривые отклика ячеечной модели при различном числе

ячеек на ступенчатое возмущение

Раздел 3.4. Диффузионная модель

Поршневой режим движения жидкостей, рассмотренный нами при выводе уравнения модели идеального вытеснения, в реальных процессах реализуется не всегда. На самом деле в реальных процессах жидкость в различных направлениях перемещается за счет следующих явлений:

• Турбулентности потока

• Конвективного переноса.

• Поперечной неравномерности профиля скорости.

• Пристеночных эффектов, каналообразования.

• Переноса за счет молекулярной диффузии.

Будем считать, что все отклонения режима движения от поршневого режима, могут быть сведены к переносу в обратном направлении, за счет влияния конвективной диффузии, или осевой дисперсии.

На рис 3.4.1. приведена схема потоков в таком аппарате:

Р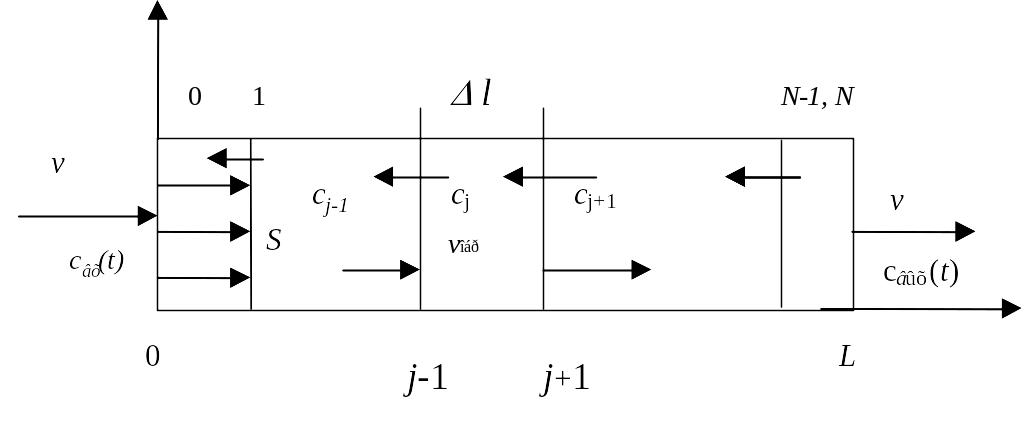 ис.3.4.1. Схема потоков в аппарате, описываемом диффузионной моделью.

V=SL – объем аппарата, S=d²/4 – площадь поперечного сечения, L – длина аппарата.

Стрелками в обратном направлении обозначен перенос вещества в обратном направлении за счет конвективной диффузии или продольной дисперсии.

Составим уравнение материального баланса для аппарата с приведенной структурой потоков.

Поток вещества за счет турбулентной диффузии описывается уравнением, подобным уравнению диффузии Фика:

(3.4.1)

Где J_обр- поток вещества в обратном направлении.

D_M – коэффициент обратного переноса массы за счет турбулентной диффузии.

Составим уравнение материального баланса для элементарного объема аппарата, ограниченного сечениями j-1 и j+1, расположенными на расстоянии l.

Приход вещества в рассматриваемый объем складывается из прихода за счет конвективного переноса и за счет обратного потока из предшествующего объема аппарата:

(3.4.2)

Накопление массы в рассматриваемом элементарном объеме будет равно интегралу от разности входящего и выходящего потоков в объем:

(3.4.3)

Перейдем теперь от накопления массы в объеме к изменению концентрации. Для этого разделим обе части уравнения на величину элементарного объема V=Sl и продифференцируем обе части уравнения по времени. С учетом того, что производная от интеграла по аргументу равна подинтегральному выражению и уравнения (3.4.2) для потоков прихода и расхода вещества, уравнение принимает следующий вид:

(3.4.4)

Рассмотрим пределы слагаемых правой части уравнения (3.4.4) при l0.

(3.4.5)

Подставив выражения пределов из (3.4.5) в (3.4.4) получим окончательно уравнение диффузионной модели в следующем виде:

(3.4.6)

Уравнение записано как дифференциальное уравнение в частных производных, так как концентрация является функцией двух независимых переменных с(l,t). В дальнейшем мы не будем это писать для сокращения записей но будем постоянно иметь в виду, что с=с(l,t).

Приведем уравнение к безразмерному виду с помощью следующих подстановок:

=l/L, где l – текущая длина, а L – полная длина аппарата. Тогда Ld=dl и dl²=L²d². С использованием этих подстановок уравнение диффузионной модели может быть преобразовано к следующему виду:

(3.4.7)

Умножим обе части уравнения (3.4.7) на величину

- среднее время пребывания в аппарате. В итоге получим:

(3.4.8)

Рассмотрим предельное выражение уравнения диффузионной модели при Ре . При Ре  1/Ре0. Таким образом, уравнение диффузионной модели превращается в следующее уравнение:

,

которое, является уравнением модели идеального вытеснения.

Для решения уравнения диффузионной модели преобразуем его по Лапласу по переменной t. В итоге получим:

(3.4.9)

Уравнение (3.4.9) представляет собой однородное обыкновенное дифференциальное уравнение с постоянными коэффициентами.

Его решение имеет вид:

((3.4.10)

Где K₁ и K₂ корни характеристического уравнения, соответствующего дифференциальному уравнению (3.4.9).

. Характеристическое уравнение для уравнения (3.4.9) будет иметь вид:

(3.4.11

Найдем корни этого характеристического уравнения:

(3.4.12

Обозначим первое слагаемое в уравнении (3.4.12 через , а второе через .

Корни характеристического уравнения можно записать в следующем виде:

, .

Тогда общее решение уравнения (3.4.9) для случая когда (корни различные и действительные) можно записать в виде:

(3.4.13

где - и – постоянные интегрирования, определяемые из граничных условий.

Если (корни равные и действительные)

(3.4.14

Если корни комплексные - - действительная часть, i -мнимая часть, то решение имеет вид:

(3.4.15

Постоянные интегрирования можно определить из граничных условий, выражающих закон сохранения массы на входе и выходе из аппарата, указанной на схеме рис.3.4.1. Приход массы в эту ячейку складывается из прихода с входным потоком и прихода за счет обратного диффузионного потока. Расход складывается из конвективного уноса массы в последующие объемы аппарата. Из равнения материального баланса на входе в аппарат следует:

(3.4.15

Где и - концентрация и ее производная по безразмерной длине на воде в аппарат,

- концентрация трассера во входном потоке.

И уравнения (3.4.15) следует, что концентрация вещества во входном сечении аппарата не равна концентрации во входном потоке, Она изменяется скачкообразно за счет действия обратного перемешивания.

Из уравнения материального баланса в выходном сечении аппарата определяем 2-е граничное условие:

(3.4.16).

Используя граничные условия (3.4.15) и (3.4.16) можно определить постоянные интегрирования и в уравнении (3.4.13). Для этого нужно определить значение концентрации и ее производной по длине во входном сечении при , , а также значение производной при . Подставив эти значения в уравнения (3.4.15) и (3.4.16), определим значения постоянных интегрирования

(3.4.17)

где

Подставив найденные выражения для постоянных интегрирования в уравнение (3.4.13), найдем уравнение для зависимости концентрации от длины и переменной Лапласа в следующем виде:

(3.4.18)

найдем передаточную функцию аппарата с конечными размерами. Для этого вычислим значение выходной концентрации, положив в уравнении (3.4.19) =1.

В итоге получим:

(3.4.19)

откуда найдем передаточную функцию:

(3.4.20)

Критерий Пекле и коэффициент продольной диффузии , являющиеся параметрами диффузионной модели определяют экспериментально с использованием экспериментов с трассерами. Методы определения параметров модели по экспериментальным данным мы рассмотрим ниже.

Рассмотрим решение уравнения диффузионной модели для аппарата бесконечно больших размеров. В таком аппарате возмущения не доходят до его границ. Поэтому можно считать, что концентрация на входе в аппарат равна концентрации во входном потоке, а концентрация на выходе равна нулю, при . Для этого случая граничные условия будут иметь вид:

, так как . Для этих значений граничных условий решение уравнения диффузионной модели будет иметь следующий вид:

(3.4.21)

Концентрация на выходе из аппарата будет равна:

(3.4.22)

Откуда передаточная функция аппарата бесконечно больших размеров будет равна:

(3.4.23)