Лекции на тему «Аналитическая геометрия»

Раздел III. Основы аналитической геометрии

Глава 4. Прямя и плоскость

4.1. Прямая на плоскости

4.1.1. Способы задания прямой на плоскости

1 Способ: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Дано. Точка , L – прямая на плоскости. Вектор . Всякий ненулевой вектор перпендикулярный прямой называется нормальным вектором.

Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору имеет вид:

(4.1),

преобразовав которое, получаем общее уравнение прямой:

(4.2),

где А, В, С – постоянные коэффициенты, причем , ,

Если , то уравнение (4.2) преобразуется к виду или

(4.3) – уравнение прямой в отрезках.

а – отрезок, который отсекает прямая на оси ОХ, b – соответственно на ОУ.

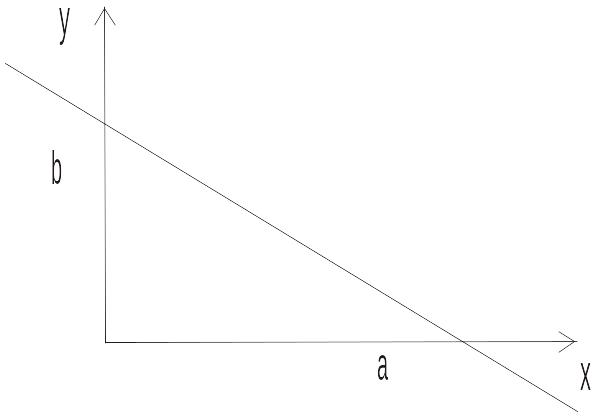
Пример 4.1. Составить уравнение прямой, проходящей через точку А (2; – 3) перпендикулярно к вектору . Найти отрезки отсекаемые прямой на координатных осях.

Пример 4.2. Составить уравнение прямой, проходящей через точку А (2; –1), если эта прямая отсекает от положительной полуоси Оу отрезок, вдвое больший, чем на положительной полуоси Ох.

2 Способ: уравнение прямой, проходящей через данную точку параллельно данному вектору.

Дано. Точка , L – прямая на плоскости. Вектор .

Всякий ненулевой вектор параллельный прямой (или лежащий на этой прямой) называется направляющим вектором.

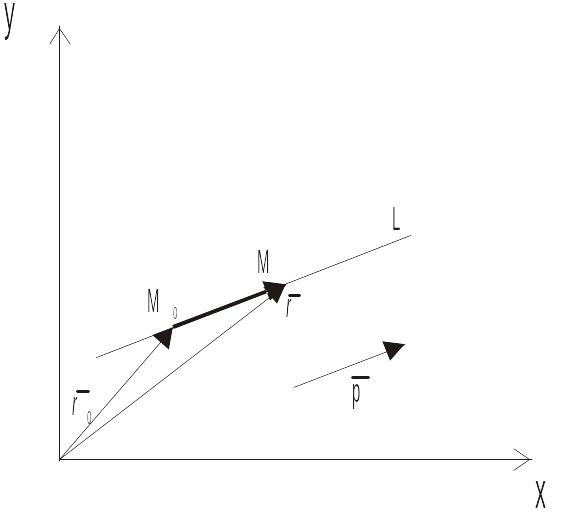
Уравнение прямой, проходящей через данную точку параллельно данному вектору можно записать в форме:

(4.4) – параметрическое уравнение прямой, где t – переменная, которая может принимать любые действительные значения и называется параметром.

Если , то, исключая параметр t из уравнения (4), получим

(4.5) – каноническое уравнение прямой.

Пример 4.3. Составить уравнение прямой, проходящей через точку М (– 4; 2) параллельно вектору , где А (– 2; 1), В (3; 5).

Замечание.

• – прямая // оси ОХ.

• – прямая // оси ОУ.

3 Способ: уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом k.

Д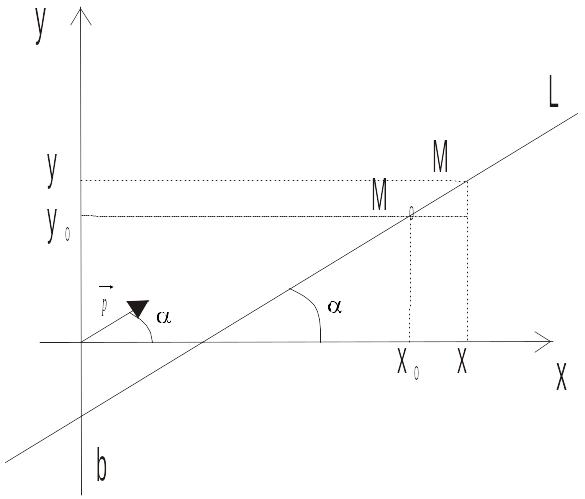 ано. Точка , L – прямая на плоскости. k=tg (угловой коэффициент прямой), где – угол наклона прямой к положительному направлению оси ОХ.

Уравнение прямой, проходящей через данную точку с заданным угловым коэффициентом k имеет вид:

(4.6).

Из (4.6), обозначая , получим

(4.7) – уравнение прямой с угловым коэффициентом.

В частности, если угол =0, то и угловой коэффициент k = 0; если , то k=tg – не существует ( при ).

Пример 4.4. Составим уравнение прямой, проходящей через точку А (3;–2) под углом 135° к оси Ох.

4 Способ: уравнение прямой, проходящей через две данные точки.

Даны две точки М₁ ( ), М₂ ( ) принадлежащие прямой L.

Уравнение прямой L, проходящей через две данные точки имеет вид:

(4.8).

Пример 4.5. Составить уравнение прямой, проходящей через точки А (–5; 4) и B (3; –2).

Решение. По уравнению (4.8):

или , 8∙(у – 4) = –6∙(х + 5),

откуда после преобразований получим: .