Першин В.Ф., Селиванов Ю.Т. Расчет на прочность тонкостенных оболочек вращения и толстостенных цилиндров
.pdf
В технике высоких давлений, кроме посадки, применяется так называемое автофретирование, которое заключается в |
|||||
предварительной нагрузке цилиндра внутренним давлением, бóльшим рабочего, с таким расчетом, чтобы во внутренних |
|||||
слоях цилиндра возникали пластические деформации. После снятия давления во внешних слоях цилиндра сохраняются |
|||||
упругие напряжения растяжения, а во внутренних слоях возникают деформации сжатия (см. рис. 12). |
|||||
В |
дальнейшем |
при |
|
||
нагрузке |
|
|
цилиндра |
|
|
давлением |
|
остаточные |
|
||
напряжения |
суммируются с |
σt |
|||
рабочим |
|
так, |
что |
во |
|
внутренних |
слоях |
имеет |
σr |
||
место чистая разгрузка. 
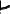
Материал цилиндра не 
получает пластических 
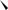
деформаций, если только 
рабочее давление не превышает давление предварительного обжатия.
|
|
|
|
|
ПРИМЕР |
Рис 12 |
|
|
|
|
|
|
|
РАСЧЕТА ЭЛЕМЕНТА ТОНКОСТЕННОЙ |
|
|
|
|
|
|
ОБОЛОЧКИ ВРАЩЕНИЯ. КОНИЧЕСКАЯ ЧАСТЬ |
||
|
|
|
|
|
Схема показана на рис. 13. |
||
|
|
|
|
|
|||
|
|
|
|
|
Дано: |
толщина стенки δ = 0,02 м; |
|
10 |
|||||||
давлениевнутриоболочкиР= 0,2 МПа; удельныйвесжидкостиγ = 1,5 104 н⁄ м3. |
|||||||
0,25 |
|
|
|
|
|
||
|
|
|
|
|
Решение: Рассмотрим отсеченную часть с действующими на нее силовыми |
||
|
|
|
|
|
факторами (см. рис. 4). |
||
|
|
B |
I сечение проходит через т. А |
||||
|
|
R1 = 0; R2 = 0; σs = 0; σt = 0. |
|||||
|
45o |
||||||
|
II сечение располагается на расстоянии х = 0,15 м. |
||||||
|
|
|
|
|
|||
A |
|
|
Высота столба жидкости над сечением v = 10 - 0,15 = 9,85 м. |
||||
|
|||||||
|
|
|
|
|
Давление q = P +vγ = 0,2 106 +9,85 1,5 104 = 347750 н/м2 . |
||
В соответствии с уравнением равновесия нижней отсеченной части оболочки (13) имеем
σs 2πRt δcos α − γ 13 Rt2 x −qπRt2 = 0;
σs2π 0,15 0,02cos45o −1,5 104 13 π 0,153 −347750π 0,152 =0
σs ≈1,85 МПа
В соответствии с формулой Лапласа (1) имеем,
σt |
+ |
σs |
= q |
R |
= |
Rt |
= |
0,15 |
= 0,212 м. . |
|
|
|
|||||||
R1 |
|
R2 |
h |
1 |
|
cosα |
0,707 |
|
|
|
|
|
|
||||||
Радиус кривизны R2 для конуса равен ∞
0,212σt = 3477500,02 ; σt ≈ 3,69 МПа.
III сечение проходит через т. В.
х= 0,25 м;
v= 10 - 0,25 = 9,75 м;
q = P + vγ = 0,2 106 +9,75 1,5 104 = 346250 н/м2 .
Решая уравнение равновесие (12) получим:
σs 2πRt δcosα − γ 13 πRt2 x −qπRt2 = 0;
σs 2π 0,25 0,02 cos45o −1,5 104 13 π 0,253 −346250 π 0,252 = 0;
|
|
|
|
|
|
σs ≈ 3,07 МПа. . |
|
|
|||||
В соответствии с формулой Лапласа |
|
|
|
|
|
|
|
|
|
|
|
|
|
σt |
+ |
|
σs |
= q ; R |
= |
|
Rt |
= |
0,25 |
|
= 0,354 м; |
||
|
|
|
|
|
|||||||||
R1 |
|
|
R2 |
h |
1 |
|
cosα |
0,707 |
|
||||
|
|
|
|
|
|||||||||
|
|
|
σt |
= |
346250; |
σt |
≈ 6,13 |
МПа. |
|||||
|
0,354 |
||||||||||||
|
|
0,02 |
|
|
|
|
|
|
|||||
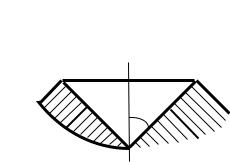
Эпюра напряжений показана на рис. 14.
Рис. 14
|
σs |
|
|
|
σt |
|
|
|
|
|
|
|
|
|
|
|
|
СПИСОК ЛИТЕРАТУРЫ |
|
|
|
||||||
1 Феодосьев В. И. Сопротивлениематериалов. М.: Наука, 1986. 512 с. |
|
|
|
||||||||||
|
3,07 |
|
45° |
|
|
6,13 |
|
|
|
|
|
||
2 Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высшая школа, 1989. 623 с. |
|||||||||||||
3 Степин П. А. Сопротивление материалов. М.: Высшая школа, 1983. 303 с. |
|
|
|||||||||||
4 |
1,85 |
|
|
|
3,69 |
|
|
|
|
|
|
|
|
Миролюбов И. Н. Пособие по решению задач по сопротивлению материалов: Учебное пособие для технических |
|||||||||||||
вузов. М.: Высшая школа, 1985. 399 с. |
|
|
|
|
|
|
|
|
|
||||
1. |
Бояршинов С. В. Основы строительной механики машин. М.: Машиностроение, 1973. 456 с. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ПРИЛОЖЕНИЕ |
|
|
|
|
|
|
1 ДАННЫЕ ДЛЯ ЗАДАНИЯ |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цифры |
Схема |
|
L = L1, |
r, м |
|
R = xr, м |
δ, см |
α, град |
Р, Мпа |
γ, кгс/см3 |
|
|
|
шифра |
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
I |
|
3 |
0,5 |
|
1,2 |
1 |
45 |
0,1 |
1 10-3 |
||
|
2 |
II |
|
4 |
0,3 |
|
1,05 |
0,5 |
50 |
0,11 |
0,5 10-3 |
||
|
3 |
III |
|
5 |
0,35 |
|
1,1 |
0,6 |
75 |
0,19 |
1,2 10-3 |
||
|
4 |
IV |
|
6 |
0,4 |
|
1,35 |
0,9 |
55 |
0,17 |
0,6 10-3 |
||
|
5 |
I |
|
7 |
0,45 |
|
1,3 |
1,1 |
85 |
0,12 |
1,05 10-3 |
||
|
6 |
III |
|
3,5 |
0,55. |
|
1,25 |
0,7 |
80 |
0,15 |
0,8 10-3 |
||
|
7 |
IV |
|
4,5 |
0,6 |
|
1,5 |
0,75 |
60 |
0,18 |
0,6 10-3 |
||
|
8 |
II |
|
6,5 |
0,35 |
|
1,15 |
1,05 |
70 |
0,13 |
0,85 10-3 |
||
|
9 |
III |
|
4,5 |
0,5 |
|
1,4 |
0,8 |
65 |
0,16 |
0,9 10-3 |
||
|
0 |
I |
|
5,5 |
0,6 |
|
1,3 |
0,85 |
45 |
0,2 |
1,1 10-3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Буква |
а |
б |
в |
г |
д |
е |
а |
б |
шифра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
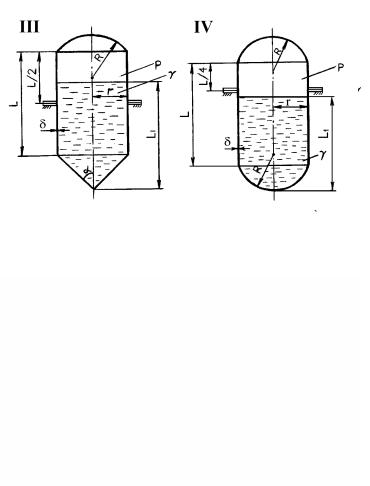
2 РАСЧЕТНЫЕ СХЕМЫ К ЗАДАНИЮ
СОДЕРЖАНИЕ |
|
ВВЕДЕНИЕ ...................................................................................... |
3 |
СОДЕРЖАНИЕ ЗАДАНИЯ ........................................................... |
3 |
ТОНКОСТЕННАЯ ОБОЛОЧКА ВРАЩЕНИЯ. ОБЩИЕ |
|
ПОЛОЖЕНИЯ …………………………………………………… |
4 |
СФЕРИЧЕСКАЯ ОБОЛОЧКА .............................................……….. |
6 |
ЦИЛИНДРИЧЕСКАЯ ОБОЛОЧКА ..................................………..... |
7 |
КОНИЧЕСКАЯ ОБОЛОЧКА ......................................………........... |
8 |
ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ. ОБЩИЕ ПОЛОЖЕНИЕ |
10 |
СОСТАВНЫЕ ЦИЛИНДРЫ. АВТОФРЕТИРОВАНИЕ. |
|
|
ОБЩИЕ ПОЛОЖЕНИЯ ..........…………………………………. |
12 |
|
ПРИМЕР РАСЧЕТА ЭЛЕМЕНТА ТОНКОСТЕННОЙ |
|
|
ОБОЛОЧКИ ВРАЩЕНИЯ. КОНИЧЕСКАЯ ЧАСТЬ............. |
16 |
|
СПИСОК ЛИТЕРАТУРЫ ............................................................ |
17 |
|
ПРИЛОЖЕНИЕ |
|
|
1 |
ДАННЫЕ ДЛЯ ЗАДАНИЯ...................................................... |
18 |
2 |
РАСЧЕТНЫЕ СХЕМЫ К ЗАДАНИЮ................................... |
19 |