2.3.2 Поверхні обертання

Поверхню, утворену обертанням твірної лінії навколо нерухомої прямої – осі, називають поверхнею обертання.

П оложення точок на кривій поверхні, подібно до положення точок на гранній поверхні, визначаються за допомогою ліній – прямих або кривих, які проходять через ці точки на заданій поверхні (рис. 2.27).

Рисунок 2.27 Побудова точок на поверхні конуса двома способами

3.2.1 Перерізи поверхонь обертання проекційними площинами

П ри перерізі циліндра площиною, залежно від її положення відносно осі циліндра у перерізі можуть утворитися коло, еліпс, чотирикутник (рис. 2.28).

При перерізі конуса площиною, окрім трикутника, можливі всі плоскі криві другого порядку: коло, еліпс, парабола і гіпербола (2.29).

З агальний порядок розв’язку задач є наступний:

1. проводять ряд допоміжних площин, які перетинають задану поверхню і площину;

2. будують лінії перетину допоміжних площин з заданою поверхнею і площиною;

3. в перетині знайдених ліній відмічають точки шуканої лінії перетину.

3.3.3 Взаємний перетин поверхонь

П еретин поверхонь між собою приводить до утворення ліній – кривих чи прямих, які є геометричним місцем точок, спільним для обох поверхонь. Ці лінії називаються лініями взаємного перетину або лініями переходу. Для побудови лінії перетину потрібно відшукати такі точки, які належали б одночасно двом заданим поверхням, що перетинаються. З’єднавши ці точки в певній послідовності, одержимо шукану лінію перетину. Лінії взаємного перетину можуть бути плоскими і просторовими.

Для визначення точок, які належать лінії перетину поверхонь тіл, застосовують метод посередників. Посередником може бути площина або сфера (спосіб площин і спосіб сфер). Спосіб допоміжних площин є універсальний і може успішно використовуватися в більшості випадків (рис. 2.30).

Алгоритм розв’язку задачі на визначення лінії перетину двох поверхонь наступний:

1. вводимо допоміжну січну площину, яка перетинає кожну із заданих поверхонь по найбільш простих і вигідних для побудови лініях;

2. визначаємо лінії перетину допоміжної площини із кожною із заданих поверхонь;

3. знаходимо точки перетину побудованих ліній.

2.4 Завдання до розділу 2

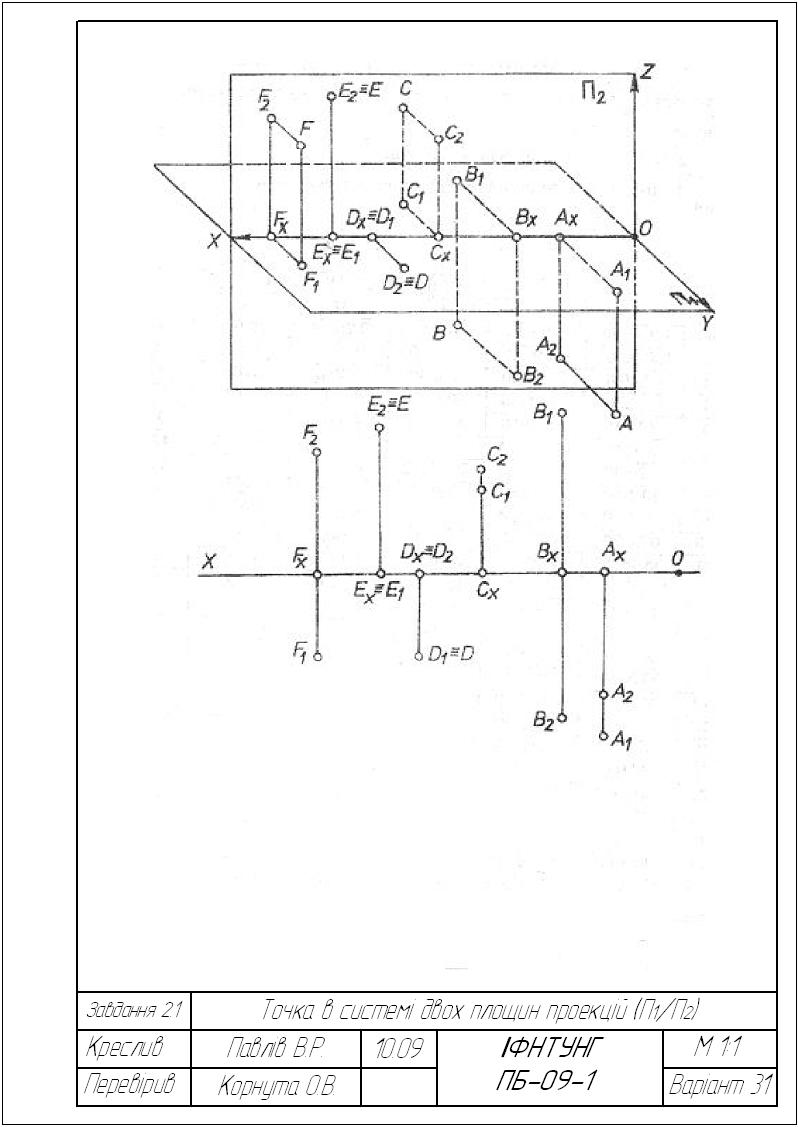
Завдання 2.1. Точка в системі П_1, П₂

1. Побудувати комплексне креслення (епюр) та наочне зображення указаних точок у системі двох площин проекцій. Вказати місце їх розташування.

2. Варіанти завдання взяти з табл. 2.1.

3. Приклад виконання завдання подано на рис. 2.31.

Таблиця 2.1 – Варіанти завдання 2.1

№ варіанта	Координати точок, мм
	А	В	С	D	E	F
	15,-30,0	35,-20,35	65,40,30	75,0,40	85,40,-20	95,-20,-30
	10,40,20	30,20,-30	45,0,-25	60,-20,0	75,-20,-35	90,-40,25
	5,20,30	15,-40,20	25,0,-30	35,-40,-30	65,20,-35	85,30,0
	10,40,-25	25,20,35	90,-40,-20	70,-20,30	55,0,25	35,20,0
	15,-20,30	2,-40-25	45,0,30	60,20,45	75,40,0	90,40,-20
	10,-40,30	25,-40,0	40,-20,-45	55,0,-30	75,40,25	85,20,-30
	20,40-30	30,-40,-40	50,-20,25	65,20,0	75,0,35	90,20,30
	10,20,0	25,20,-35	40,-20,-35	55,-40,30	80,20,30	90,0,30
	10,-20,-30	25,0,-35	35,-20,0	50,20,-25	70,40,40	80,-40,30
	10,0,-30	90,-20,0	20,-20,-30	45,40,-30	60,20,35	75,-20,35
	95,-20,-30	85,40,-20	75,0,30	65,40,30	35,-20,35	15,-30,0
	90,-40,2	75,-20,-35	60,-20,0	45,0,-25	30,20,-30	10,40,20
	85,30,0	65,20,-35	35,-40,-30	25,0,-30	15,-40,20	5,20,30
	35,20,0	55,0,25	70,-20,30	90,-40,-20	25,20,35	10,40,-25
	90,40,-30	75,40,0	60,20,45	45,0,30	25,-40-25	15,-20,30
	85,20,-30	75,40,25	55,0,-30	40,-20,-45	25,-40,0	10,-40,30
	90,20,30	75,0,35	65,20,0	50,-20,25	30,-40,-40	20,40,-30
	90,0,30	80,20,30	55,-40,30	40,-20,-35	25,20,-35	10,20,0
	80,-40,30	70,40,40	50,20,-25	35,-20,0	25,0,-35	10,-20,-30
	75,-20,35	60,20,35	45,40,-30	20,-20,-30	90,20,0	10,0,-30
	10,0,-30	90,-20,0	20,-20,-30	45,40,-30	60,20,35	75,-20,35
	10,-20,-30	25,0,-35	35,-20,0	50,20,-25	70,40,40	80,-40,30
	10,20,0	25,20,-35	40,-20,-35	55,-40,30	80,20,30	90,0,30
	20,40,-30	30,-40,-40	50,-20,25	65,20,0	75,0,35	90,20,30
	10,-40,30	25,-40,0	40,-20,-45	55,0,-30	75,40,25	85,20,-30
	85,30,0	65,20,-35	35,-40,-30	25,0,-30	15,-40,20	5,20,30
	90,40, 30	75,40,0	60,20,45	45,0,30	25,-40,-25	15,-20,30
	10,-40,30	25,-40,0	40,-20,-45	55,0,-30	75,40,25	85,20,-30

Точка	Координати			Місце знаход.
	X	Y	Z
A	20	40	-30	IV чв.
B	30	-40	-35	III чв.
C	50	-20	25	II чв.
D	65	20	0	на П1
E	75	0	35	наП2
F	90	20	30	I чв.

Рис.2.31 – Приклад виконання завдання 2.1

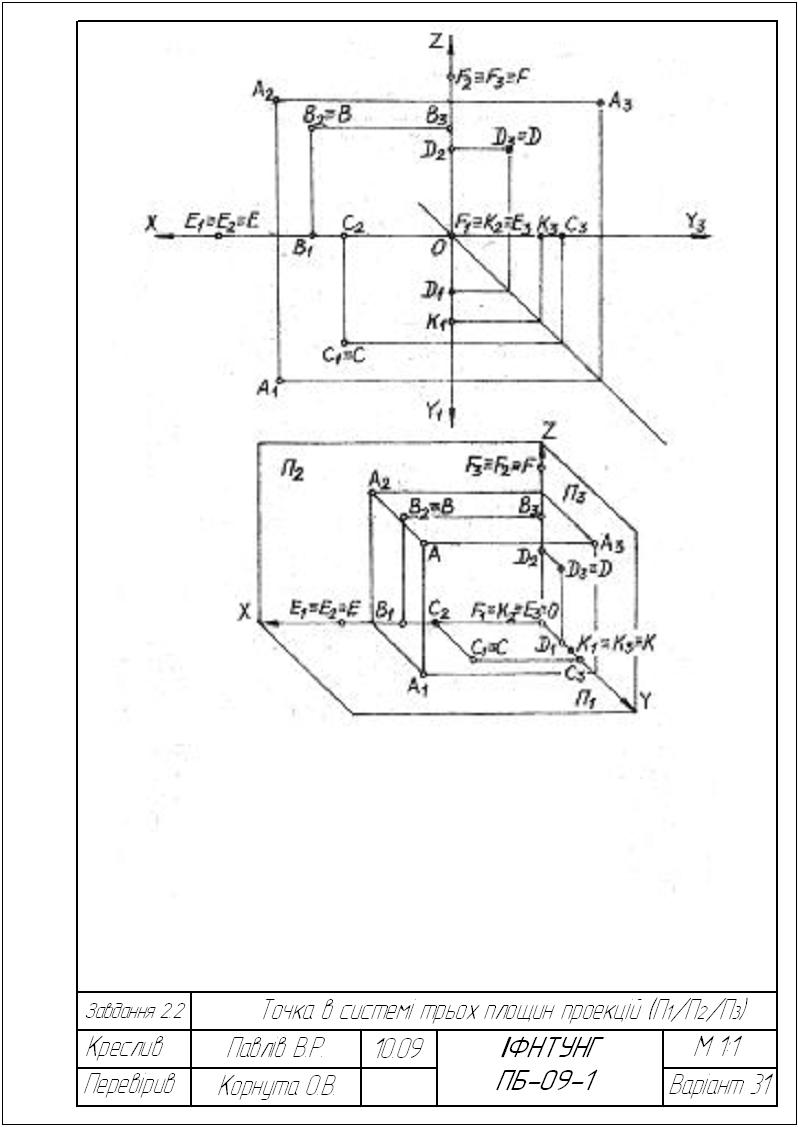
Завдання 2.2. Точка в системі П_1, П_2, П₃.

1. Побудувати комплексне креслення (епюр) та наочне зображення указаних точок у системі трьох площин проекцій. Вказати місце їх розташування.

2. Варіанти завдання взяти з табл. 2.2.

3. Приклад виконання завдання подано на рис. 2.32.

Таблиця 2.2 – Варіанти завдання 2.2

№ варіанта	Координати точок, мм
	А	В	С	D	E	F
	60,50,50	50,0,40	40,40,0	0,20,30	70,0,0	0,0,60
	50,0,40	60,50,50	0,20,30	40,40,0	0,0,60	70,0,0
	40,40,0	60,50,50	50,0,40	0,30,0	70,0,0	0,0,60
	0,20,30	60,55,55	50,0,45	40,40,0	65,0,0	0,20,0
	70,0,0	55,50,50	50,0,40	30,40,0	0,15,30	0,0,65
	50,0,40	60,50,50	0,25,0	0,0,65	0,20,30	40,40,0
	0,20,30	50,0,40	60,50,50	40,40,0	70,0,5	0,30,0
	40,40,0	65,50,50	0,30,0	50,0,40	0,20,30	0,0,60
	30,40,0	55,50,50	50,0,40	0,25,0	0,0,65	0,15,30
	0,20,30	40,40,0	50,0,35	60,50,50	0,30,0	0,0,60
	55,45,45	45,0,35	55,45,0	0,25,25	50,0,0	0,0,65
	45,0,45	60,50,45	0,25,35	35,35,0	0,0,15	30,0,0
	50,0,40	60,45,50	0,30,0	0,0,62	0,20,35	35,35,0
	65,0,0	60,50,50	45,0,40	30,45,0	0,20,30	0,0,20
	50,0,20	65,45,45	0,25,35	50,50,0	0,0,20	10,0,0
	60,50,50	50,0,40	40,40,0	0,20,30	70,0,0	0,0,60
	50,0,40	60,50,50	0,20,30	40,40,0	0,0,60	70,0,0
	40,40,0	60,50,50	50,0,40	0,30,0	70,0,0	0,0,60
	0,20,30	60,55,55	50,0,45	40,40,0	65,0,0	0,20,0
	70,0,0	55,50,50	50,0,40	30,40,0	0,15,30	0,0,65
	50,0,40	60,50,50	0,25,0	0,0,65	0,20,30	40,40,0
	0,20,30	50,0,40	60,50,50	40,40,0	70,0,5	0,30,0
	40,40,0	65,50,50	0,30,0	50,0,40	0,20,30	0,0,60
	30,40,0	55,50,50	50,0,40	0,25,0	0,0,65	0,15,30
	0,20,30	40,40,0	50,0,35	60,50,50	0,30,0	0,0,60
	55,45,45	45,0,35	55,45,0	0,25,25	50,0,0	0,0,65
	45,0,45	60,50,45	0,25,35	35,35,0	0,0,15	30,0,0
	50,0,40	60,45,50	0,30,0	0,0,65	0,20,35	35,35,0

Рис.2.32 – Приклад виконання завдання 2.2

Точка	Координати			Місце знаход.
	X	Y	Z
A	40	34	30	І окт.
B	30	0	25	на П2
C	25	25	0	на П1
D	0	15	20	на П3
E	55	0	0	на осі 0X
F	0	0	35	на осі 0Z
K	0	20	0	на осі 0Y

Завдання 2.3. Перетин прямої з площиною

1. Побудувати точку перетину прямої LM з площиною трикутника АВС.

2. Визначити видимість прямої LM відносно площини трикутника АВС вважаючи площину непрозорою.

3. Дані для свого варіанту взяти з таблиці 2.3.

4. Приклад завдання зображено на рисунку 2.33.

Таблиця 2.3 – Варіанти завдання 2.3

№ варіанта	Координати точок, мм
	А(x,y,z)	В(x,y,z)	С(x,y,z)	L(x,y,z)	M(x,y,z)
1	90,10,10	70,60,60	20,25,25	80,55,5	30,15,65
2	95,20,10	50,10,60	20,60,10	70,30,55	45,35,0
3	90,50,40	65,10,60	5,30,10	50,55,65	50,5,10
4	95,15,30	40,50,60	10,30,10	70,55,65	35,5,5
5	90,20,20	30,10,60	10,50,0	70,50,60	20,10,10
6	90,20,60	10,10,40	50,50,0	90,10,20	30,40,60
7	90,30,10	30,60,60	10,10,10	70,10,60	20,50,0
8	90,0,0	30,30,60	10,0,0	60,0,60	30,20,10
9	90,20,40	20,10,60	40,60,30	60,10,10	40,40,60
10	90,30,60	10,10,60	40,60,10	80,60,65	10,0,20
11	95,10,10	10,50,60	10,10,10	60,60,0	20,5,60
12	90,10,10	60,60,60	10,20,60	70,5,60	20,60,10
13	90,30,20	30,10,60	10,50,0	80,10,0	10,60,60
14	90,10,40	60,60,60	10,30,20	80,60,10	30,10,60
15	70,60,0	90,20,60	10,10,0	90,10,10	20,50,40
16	90,20,10	60,50,55	10,10,0	70,60,0	40,5,60
17	90,10,60	10,10,30	90,60,10	70,5,10	30,65,70
18	80,10,10	40,50,60	0,10,20	70,5,60	20,20,10
19	90,10,10	0,30,55	70,30,20	70,10,60	20,45,10
20	90,10,60	10,20,40	30,60,10	80,5,10	20,50,60
21	90,50,10	50,30,60	10,10,20	80,10,50	10,70,10
22	90,20,20	10,20,60	30,60,0	80,60,50	10,10,10
23	90,40,10	30,60,60	10,10,20	70,10,50	20,50,10
24	90,30,20	10,10,60	30,50,10	80,55,60	10,5,10
25	90,40,10	20,0,60	0,50,20	70,50,60	20,10,10
26	90,20,10	60,60,50	10,10,20	70,60,0	30,20,60
27	90,10,30	50,50,60	10,30,5	70,10,60	20,40,0
28	90,40,10	30,10,60	10,60,30	80,70,50	0,10,10

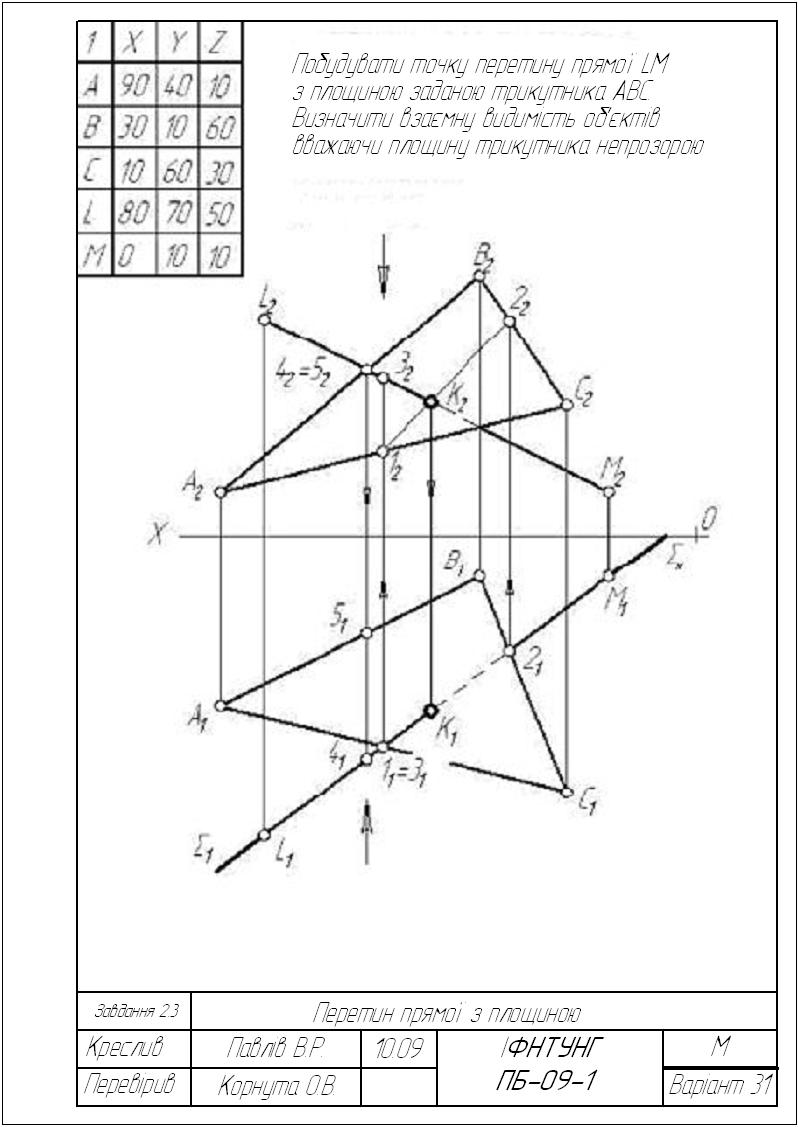
Рисунок 2.33– Приклад виконання завдання 2.3

Завдання2.4. Перетин двох площин

1. Побудувати лінію КM перетину площини трикутника АВС з площиною, яка задана паралельними прямими DE i FL.

2. Визначити взаємну видимість площин.

3. Дані до завдання взяти з таблиці 2.4. Точка L будується з умови паралельності прямих DE i FL.

4. Приклад виконання завдання подано на рис 2.34.

Таблиця 2.4 – Варіанти завдання 2.4

№ варіанта	Координати точок, мм
	А(x,y,z)	В(x,y,z)	С(x,y,z)	D(x,y,z)	E(x,y,z)	F(x,y,z)	L(x,y,z)
1	0,15,0	55,90,75	100,0,15	0,30,75	120,90,25	0,5,50	120,?,?
2	120,85,0	95,0,70	20,50,20	135,20,0	40,70,65	40,55,65	135,?,?
3	120,90,0	90,0,80	10,50,30	20,60,65	130,10,30	20,90,50	130,?,?
4	0,85,0	25,0,70	100,50,20	95,25,15	0,75,50	95,10,0	0,?,?
5	15,85,0	40,0,70	115,50,20	0,20,20	95,70,65	95,55,50	0,?,?
6	0,15,5	60,90,80	110,0,15	110,45,25	10,30,55	110,15,5	10,?,?
7	120,15,5	60,90,80	10,0,15	10,45,25	110,30,55	10,15,5	110,?,?
8	115,15,0	55,75,90	10,0,15	10,75,30	130,25,90	10,50,5	130,?,?
9	10,90,0	40,0,80	120,50,30	110,60,65	0,10,30	110,90,50	0,?,?
10	110,20,50	35,70,0	40,0,85	105,15,25	10,50,75	105,0,10	10,?,?
11	90,15,5	55,90,80	10,0,20	0,30,75	120,90,25	0,5,50	120,?,?
12	120,85,5	95,0,75	20,50,25	135,20,20	40,70,65	40,55,60	135,?,?
13	120,90,5	90,0,85	10,50,35	20,60,65	130,10,30	20,90,50	130,?,?
14	0,85,5	25,0,75	110,50,25	95,25,15	0,75,50	95,10,0	0,?,?
15	15,85,5	40,0,75	115,50,25	0,20,20	95,70,65	95,55,50	0,?,?
16	0,15,10	60,90,85	110,0,20	110,45,25	10,30,55	110,15,5	10,?,?
17	120,15,10	60,90,85	10,0,20	10,45,25	110,30,55	10,15,5	110,?,?
18	115,15,5	55,75,90	10,0,20	10,75,30	130,25,90	10,50,5	130,?,?
19	10,90,5	40,0,85	120,50,30	110,60,65	0,10,30	110,90,50	0,?,?
20	110,20,55	35,70,5	10,0,90	105,15,25	10,50,75	105,0,10	10,?,?
21	105,0,15	0,15,0	55,90,75	0,30,75	120,90,25	0,5,50	120,?,?
22	20,50,20	95,0,70	120,85,0	135,20,20	40,70,65	40,55,50	135,?,?
23	10,50,30	90,0,80	120,90,0	20,60,65	130,10,30	20,90,50	130,?,?
24	100,50,20	0,85,0	25,0,70	95,25,15	0,75,50	95,10,0	0,?,?
25	115,50,20	15,95,0	40,0,70	0,20,20	95,70,65	95,55,50	0,?,?
26	120,90,0	90,0,80	10,50,30	20,60,65	130,10,30	20,90,50	130,?,?
27	115,45,0	55,75,90	10,0,15	10,75,30	130,25,90	10,50,5	130,?,?
28	120,90,5	90,0,85	10,50,35	20,60,65	130,10,30	20,90,50	130,?,?

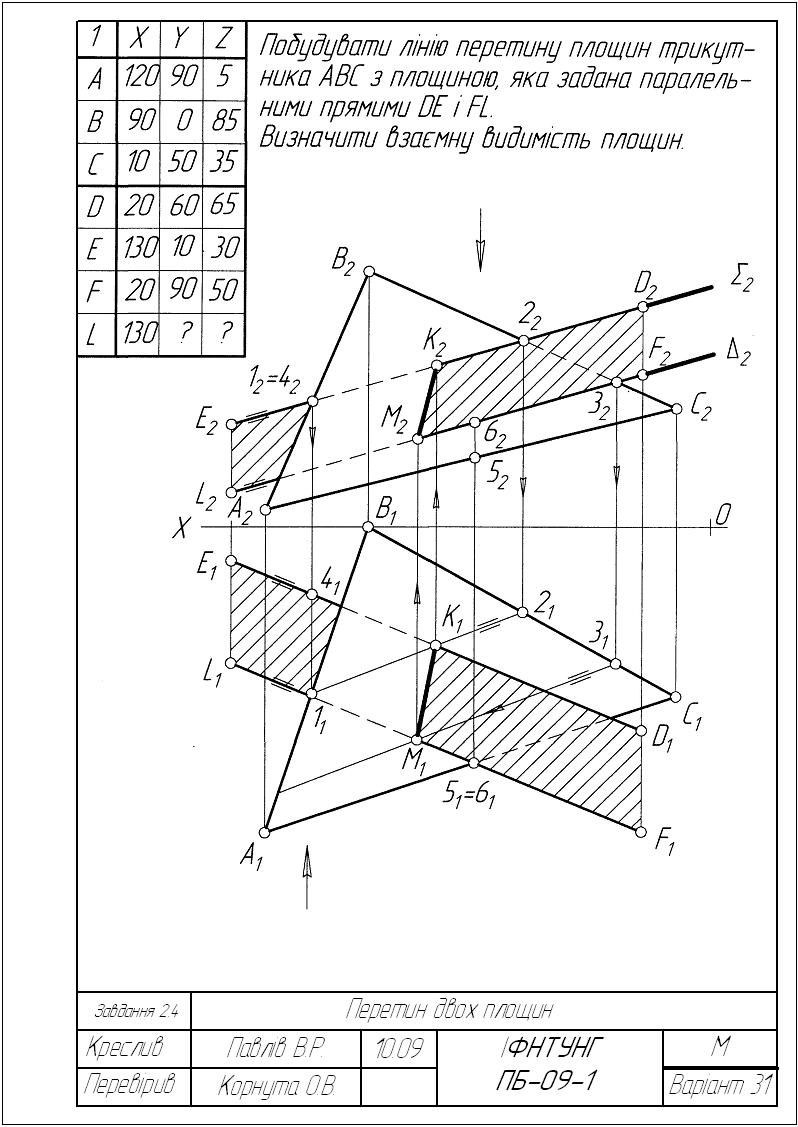
Рисунок 2.34 – Приклад виконання завдання 2.4

Завдання 2.5. Відстань від точки до площини

1. Визначити дійсну величину відстані від точки D до площини, яка задана трикутником АВС (задачу розв’язати без перетворення проекцій).

2. Дані до завдання взяти з таблиці 2.5.

3. Приклад виконання завдання подано на рис 2.35.

Таблиця 2.5 – Варіанти завдання 2.5

№ варіанта	Координати точок, мм
	А(x,y,z)	В(x,y,z)	С(x,y,z)	D(x,y,z)
1	40,80,60	0,10,10	80,35,0	70,15,40
2	10,0,0	60,65,65	95,30,10	50,70,0
3	10,0,0	55,80,70	85,30,15	40,75,0
4	0,70,60	90,25,0	20,0,15	35,60,0
5	35,70,70	85,0,0	0,10,30	10,55,0
6	35,50,70	65,10,20	0,0,25	50,0,50
7	30,70,80	75,0,15	0,15,40	15,65,0
8	40,60,80	80,10,10	0,0,35	10,40,15
9	80,0,0	35,65,70	0,10,30	45,0,70
10	75,30,15	30,70,80	0,15,30	45,0,75
11	90,60,70	0,0,25	70,15,0	55,0,45
12	35,70,70	85,0,0	0,30,10	10,0,55
13	35,70,50	65,20,10	0,25,0	50,50,0
14	30,80,70	75,15,0	0,40,15	15,0,65
15	80,0,0	35,70,65	0,30,10	45,70,0
16	50,70,70	0,0,0	85,10,30	75,55,0
17	30,50,70	0,10,0	65,0,25	15,0,50
18	45,70,80	0,0,15	75,15,40	60,65,0
19	40,60,80	0,10,10	80,0,35	70,40,15
20	10,0,0	60,65,70	95,10,30	50,0,70
21	10,0,15	55,70,80	85,35,30	40,0,55
22	0,60,70	90,0,25	20,15,0	35,0,45
23	50,70,70	0,0,0	85,30,10	75,0,55
24	30,70,50	0,0,10	65,25,0	15,50,0
25	45,80,70	0,15,0	75,40,15	60,0,65
26	0,70,60	90,25,0	20,0,15	35,60,0
27	30,70,80	75,0,15	0,15,40	15,65,0
28	35,75,65	30,0,0	0,30,10	45,70,0

Рисунок 2.35 – Приклад виконання завдання 2.5

Завдання 2.6 Заміна площини проекцій

1. Способом заміни площин проекцій визначити справжню величину трикутника АВС та кут нахилу його до горизонтальної (варіанти 1-14) або фронтальної (варіанти 15-28) площин проекцій.

2. Дані для свого варіанту взяти з таблиці 2.6.

3. Приклад виконання завдання зображено на рисунку 2.36.

Таблиця 2.6 – Варіанти завдання 2.6

№ варіанта	Координати точок, мм
	А(x,y,z)	В(x,y,z)	С(x,y,z)
1	50,70,70	0,0,0	85,10,30
2	30,50,70	0,10,0	65,0,25
3	45,70,80	0,0,15	75,15,40
4	40,60,80	0,10,10	80,0,35
5	10,0,0	60,65,70	95,10,30
6	10,0,15	55,70,80	85,35,30
7	0,60,70	90,0,25	20,15,0
8	50,70,70	0,0,0	85,30,10
9	30,70,50	0,0,10	65,25,0
10	45,80,70	0,15,0	75,40,15
11	40,80,60	0,10,10	80,35,0
12	10,0,0	60,70,65	95,30,10
13	10,0,0	55,80,70	85,30,15
14	0,70,60	90,25,0	20,0,15
15	35,70,70	85,0,0	0,10,30
16	35,50,70	65,10,20	0,0,25
17	30,70,80	75,0,15	0,15,40
18	40,60,80	80,10,10	0,0,35
19	80,0,0	35,65,70	0,10,30
20	75,30,15	30,70,80	0,15,30
21	90,60,70	0,0,25	70,15,0
22	35,70,70	85,0,0	0,30,15
23	35,70,50	65,20,10	0,25,0
24	30,80,70	75,15,0	0,40,15
25	75,15,0	30,80,70	0,30,15
26	45,70,80	0,0,15	75,15,40
27	45,80,70	0,15,0	75,40,15
28	35,50,70	65,10,20	0,0,25

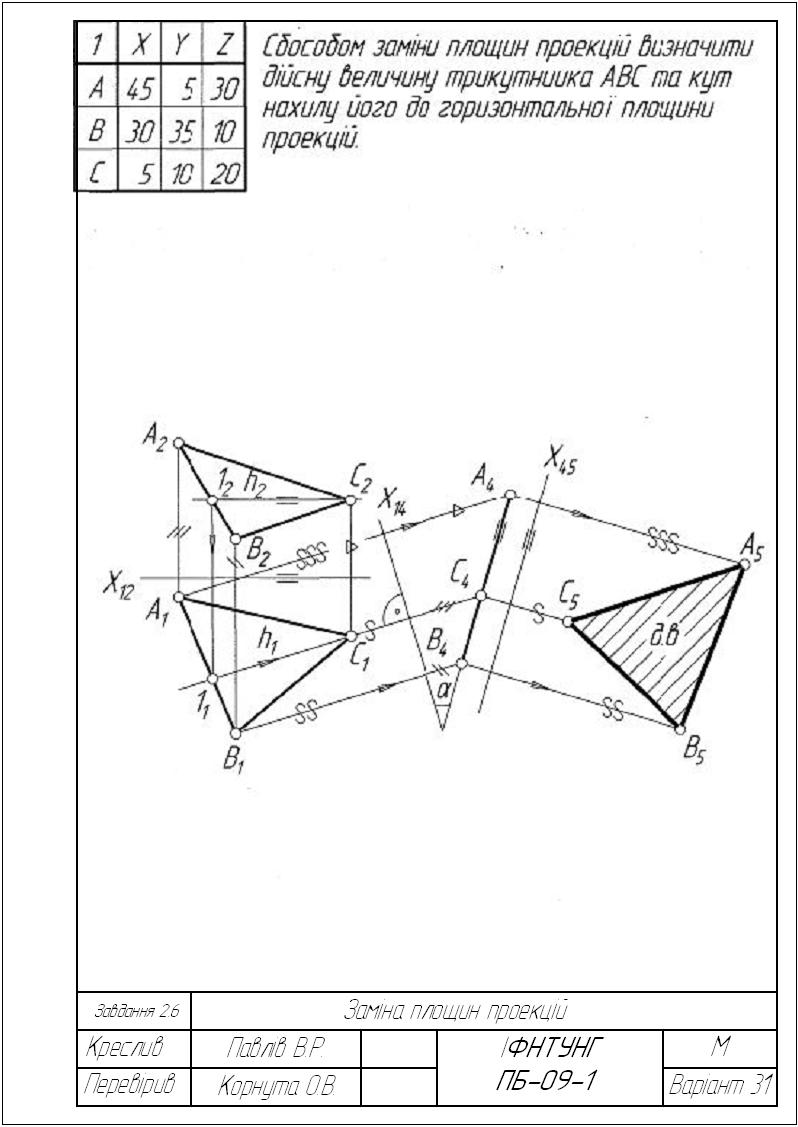
Рисунок 2.36 – Приклад виконання завдання 2.6

Завдання 2.7 Плоско-паралельне переміщення

1. Способом плоско-паралельного переміщення визначити віддаль від точки D до площини заданої трикутником АВС та кут нахилу цієї площини до горизонтальної (варіанти1-14) або фронтальної (варіанти15-28) площин проекцій.

2. Дані для свого варіанту взяти з таблиці .2.7.

3. Приклад виконання завдання зображено на рисунку 2.37.

Таблиця 2.7 – Варіанти завдання 2.7

№ варіанта	Координати точок, мм
	А(x,y,z)	В(x,y,z)	С(x,y,z)	D(x,y,z)
1	50,70,70	0,0,0	85,10,30	75,55,0
2	30,50,70	0,10,0	65,0,25	15,0,50
3	45,70,80	0,0,15	75,15,40	60,65,0
4	40,60,80	0,10,10	80,0,35	70,40,15
5	10,0,0	60,65,70	95,10,30	50,0,70
6	10,0,15	55,70,80	85,35,30	40,0,55
7	0,60,70	90,0,25	20,15,0	35,0,45
8	50,70,70	0,0,0	85,30,10	75,0,55
9	30,70,50	0,0,10	65,25,0	15,50,0
10	45,80,70	0,15,0	75,40,15	60,0,65
11	40,80,60	0,10,10	80,35,0	70,15,40
12	10,0,0	60,70,65	95,30,10	50,70,0
13	10,0,0	55,80,70	85,30,15	40,75,0
14	0,70,60	90,25,0	20,0,15	35,60,0
15	35,70,70	85,0,0	0,10,30	10,55,0
16	35,50,70	65,10,20	0,0,25	50,0,50
17	30,70,80	75,0,15	0,15,40	15,65,0
18	40,60,80	80,10,10	0,0,35	10,40,15
19	80,0,0	35,65,70	0,10,30	45,0,70
20	75,30,15	30,70,80	0,15,30	45,0,75
21	90,60,70	0,0,25	70,15,0	55,0,45
22	35,70,70	85,0,0	0,30,15	10,0,55
23	35,70,50	65,20,10	0,25,0	50,50,0
24	30,80,70	75,15,0	0,40,15	15,0,65
25	75,15,0	30,80,70	0,30,15	45,75,0
26	45,70,80	0,0,15	75,15,40	60,65,0
27	45,80,70	0,15,0	75,40,15	60,0,65
28	35,50,70	65,10,20	0,0,25	50,0,50

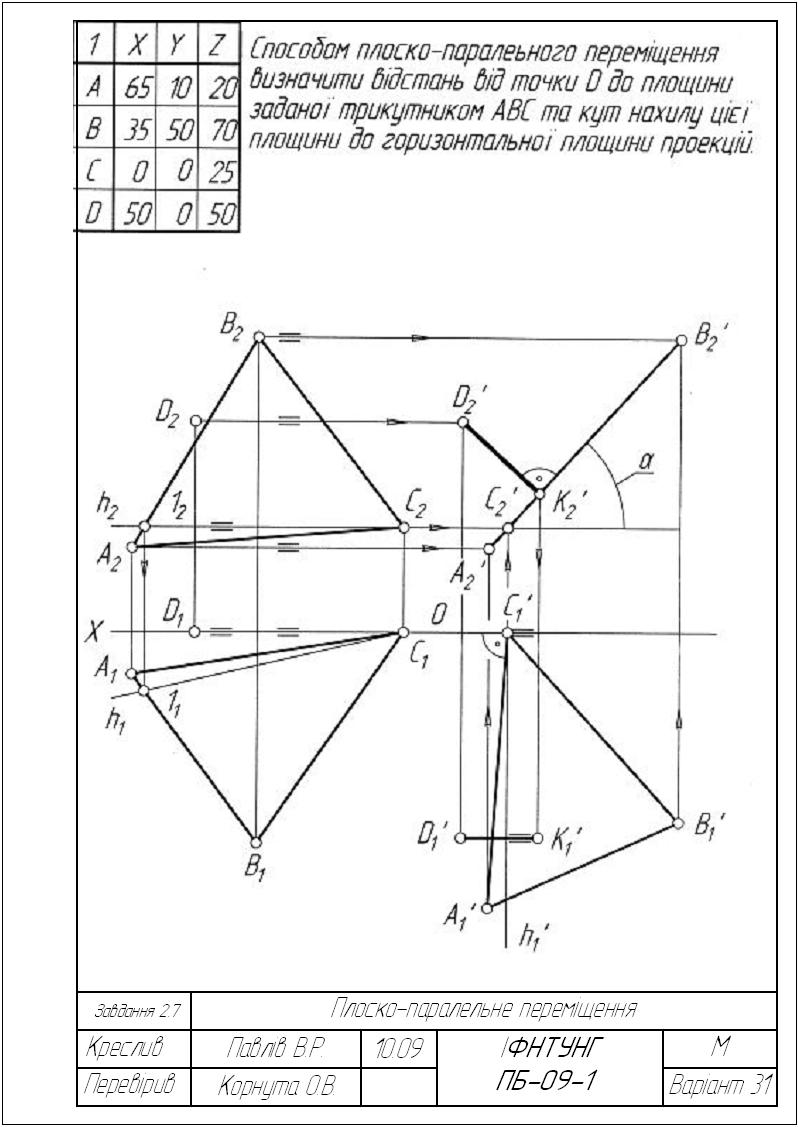
Рисунок 2.37 – Приклад виконання завдання 2.7

Завдання 2.8 Переріз правильної піраміди площиною.

1. Побудувати три проекції правильної піраміди, перерізаної фронтально-проекційною або профільною площинами

2. Варіанти завдань взяти з табл.2.8.

3. Розміри піраміди: діаметр кола, описаного навколо правильного многокутника основи дорівнює 70 мм; висота піраміди дорівнює 80 мм;

4. Приклад виконання завдання подано на рис. 2.38.

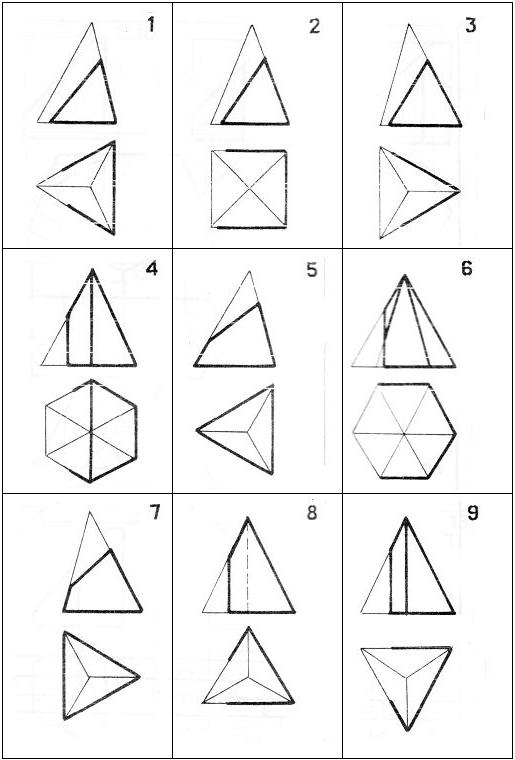Таблиця 2.8 – Варіанти завдання 2.8

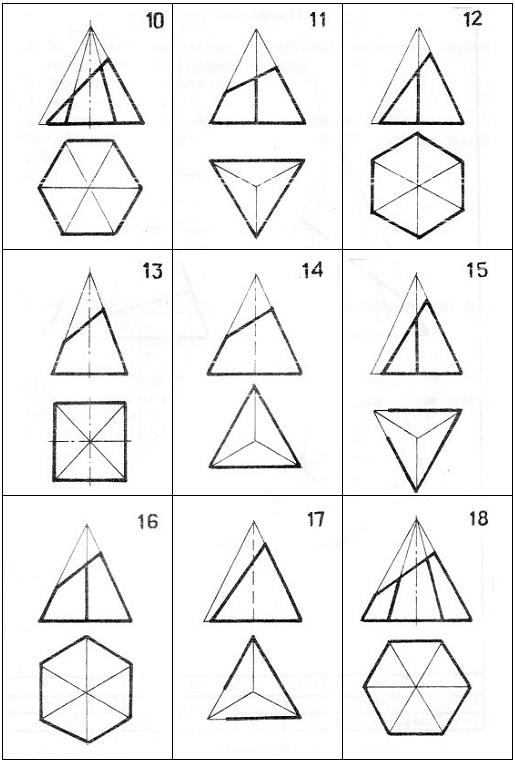Продовження таблиці 2.8

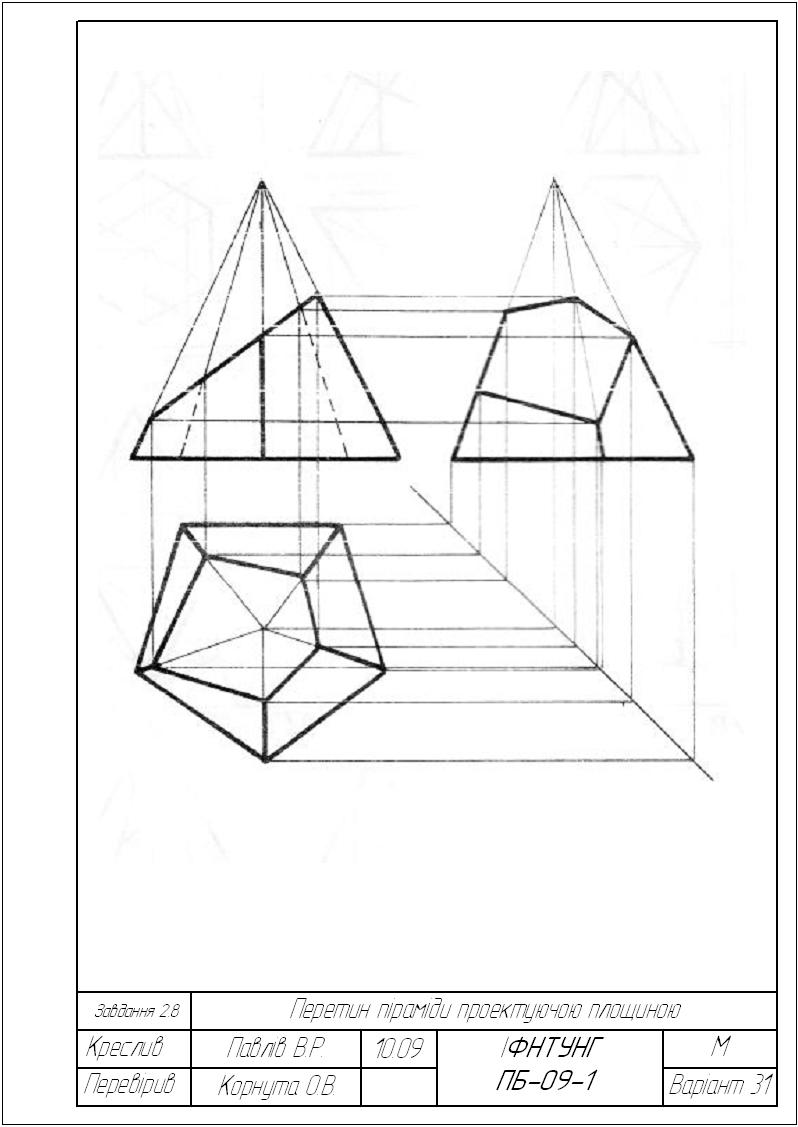
Рисунок 2.38 – Приклад виконання завдання 2.8

Завдання 2..9. Переріз неправильної піраміди площиною. Розгортка.

1. Побудувати переріз піраміди SАВС фронтально-проекційною (варіанти 1-5, 11-15, 21-25) або горизонтально-проскційкою (варіанта 6-10, 16-20, 26-30) площиною та розгортку поверхні піраміди з нанесенням на неї лінії перетину.

2. Дані до завдання взяти з табл.2.9.

3. Приклад виконання завдання подано на рис.2.39.

Схеми розташування площини

для варіантів: 1-5,11-15, 21-25 для варіантів 6-10,16-20,26-30

Таблиця 2.9 – Варіанти завдання 2.9

Варі-ант	Координати точок, мм				Параметр площини, Р
	А	В	С	S	OPх	OPy	OPz
	70,30,0	20,50,0	10,10,0	30,30,60	60		50
	70,20,0	20,50,0	10,10,0	30,30,60	60		55
	60,50,0	70,10,0	10,30,0	50,30,60	60		50
	10,20,0	40,60,0	70,20,0	50,30,50	60		60
	60,50,0	70,10,0	10,20,0	50,30,60	70		60
	70,20,0	40,60,0	10,20,0	50,30,50	90	80	
	60,50,0	70,10,0	10,30,0	50,30,60	70	70	
	70,30,0	10,10,0	20,50,0	30,30,60	80	60	
	70,20,0	10,20,0	40,60,0	50,30,50	90	80	
	40,60,0	10,20,0	70,20,0	50,30,50	60	80	
	70,30,0	20,50,0	10,10,0	30,30,60	70		50
	60,50,0	70,10,0	10,30,0	50,30,60	70		60
	70,20,0	20,50,0	10,10,0	30,30,60	70		50
	70,30,0	20,50,0	10,10,0	30,30,60	80		50
	10,20,0	40,60,0	70,20,0	50,20,50	70		50
	10,20,0	40,60,0	70,20,0	50,30,50	70	70	
	40,60,0	10,20,0	70,20,0	50,30,50	90	80	
	10,20,0	40,60,0	70,20,0	50,30,50	90	80	
	70,20,0	10,20,0	40,60,0	50,30,50	80	80	
	10,20,0	40,60,0	70,20,0	50,30,50	80	70	
	10,20,0	40,60,0	70,20,0	50,30,50	70		70
	10,20,0	40,60,0	70,20,0	50,20,50	70		50
	70,20,0	20,50,0	10,10,0	30,30,60	80		50
	60,50,0	70,10,0	10,30,0	50,30,60	60		60
	10,20,0	40,60,0	70,20,0	50,30,50	70		60
	70,10,0	60,50,0	10,30,0	50,30,60	80	60	
	40,60,0	10,20,0	70,20,0	50,30,50	70	80	
	10,20,0	40,60,0	70,20,0	50,30,50	90	80	

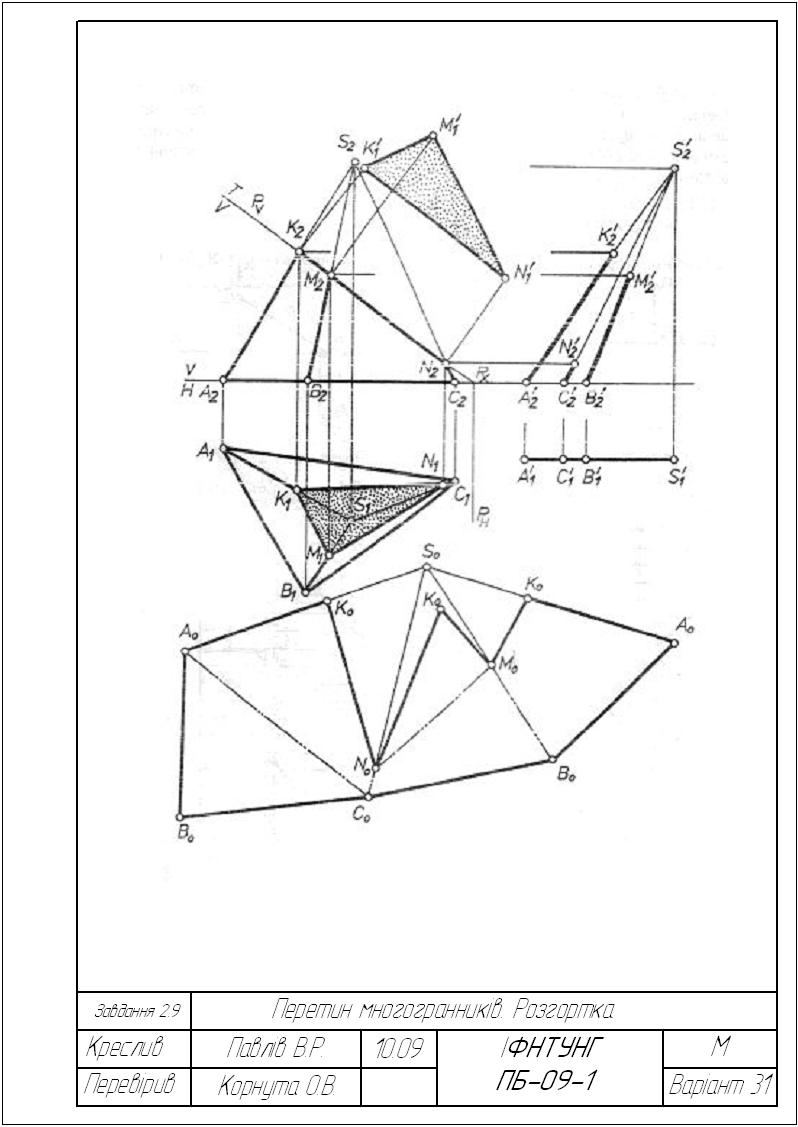
Рисунок 2.39 – Приклад виконання завдання 2.9