10

Основы теории систем связи с подвижными объектами

И.М. Орощук

4 часа

Лекция 2: ПРИНЦИПЫ ПОСТРОЕНИЯ ОПТИМАЛЬНЫХ

ПРИЕМНИКОВ РАДИОСВЯЗИ

План занятия:

Время	№ п/п	Содержание раскрываемого вопроса:
90 мин	1	Критерии принятия решений
45 мин	2	Принцип построения оптимального приемника двоичных сигналов
35 мин	3	Оптимальный прием двоичных сигналов с помощью согласованных фильтров

1. Критерии принятия решений

Простые и сложные гипотезы

1. Класс гипотез, содержащих только одну единственную гипотезу называют простой гипотезой.

2. Если число гипотез не меньше двух, такие гипотезы называют сложными.

Выборка: это n выборочных значений или реализаций случайного процесса . Число n принято называть размером или объемом выборки.

Таким образом, например, вектор , с элементами – это результат наблюдений случайного процесса , с объемом выборки n.

Однородной выборкой называют выборку x, в которой все ее элементы являются значениями одного случайного процесса с распределением и они независимы (взаимные коэффициенты корреляций для всех сечений отсчетов или коэффициентов гармоник при разложении сигнала в ряд Фурье равны нулю), то совместная плотность распределения вектора x равна

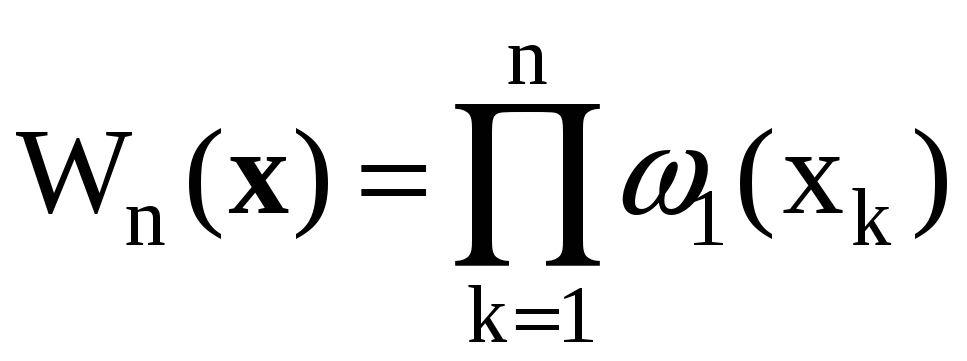, (1)

т.е. в этом случае совместная плотность вероятности выборочных значений случайного процесса равна произведению плотностей вероятности ее элементов.

В качестве примера, рассмотрим систему связи с двумя возможными состояниями, и . Приемная сторона принимает решение по значениям выборки х. Для определения двух альтернативных решений: о передаче сигнала и о передаче сигнала . Область определения , делится на две подобласти и , (рис. 1).

Таким образом, если значения выборки х попадают в подобласть принимается решение о том, что передан сигнал . В случае попадании в подобласть – принимается решение о том, что передан сигнал . При передаче сигнала область называют критической, а область – допустимой, и наоборот при передаче сигнала .

Поиск оптимального алгоритма заключается в определении границы между подобластями или (см. рис. 1).

Критерий Байеса

Для определения оптимального правила принятия решения в критерии Байеса используется оценка среднего риска принятия решения:

(2)

где – априорная вероятность гипотезы , состоящей в вероятности передачи сигнала ; – априорная вероятность гипотезы , состоящей в вероятности передачи сигнала ; – условная вероятность принятия решения при условии, если верна гипотеза ; – условная вероятность принятия решения при условии, если верна гипотеза ; – условная вероятность принятия решения при условии, если верна гипотеза ; – условная вероятность принятия решения при условии, если верна гипотеза ; – потери принятия решения , при условии, если верна гипотеза (правильное решение); – потери принятия решения , при условии, если верна гипотеза (правильное решение); – потери принятия решения , при условии, если верна гипотеза (неправильное решение); – потери принятия решения о , при условии, если верна гипотеза (неправильное решение).

Значения условных вероятностей определяются из соответствующих условных плотностей вероятностей:

(вероятность правильного решения ); (3)

(вероятность правильного решения ); (4)

(вероятность ошибки первого рода); (5)

(вероятность ошибки второго рода), (6)

где – область значений, при попадании в которую принимается решение ; – область значений, при попадании в которую принимается решение ; – условная плотность распределения выборки x, при условии, что действительно передавался сигнал ; – условная плотность распределения выборки x, при условии, что действительно передавался сигнал .

Между выражениями (3) и (5), а также между (4) и (6) существует связь:

; (7)

. (8)

Критерий Байеса заключатся в выборе границ между подоблостями и , при которых средний риск будет минимальным.

Этот критерий применим, если известны априорные данные , и условные вероятности , ; а также можно задать матрицу потерь: , , и .

Для определения границы между подобластями, с учетом выражений для условных плотностей вероятностей (3) – (8), выразим средний риск через критическую область Х₁:

. (8)

Так как это постоянные величины, не зависящие от выбора границ между подоблостями и , минимум среднего риска будет, если интеграл будет положительным:

. (9)

Откуда

или

. (10)

О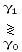тношение называется функцией отношения правдоподобия. В этом случае оптимальное правило принятия решения по критерию Байеса определяется следующим условием: принимается решение при условии, если функция отношения правдоподобия превышает порог с:

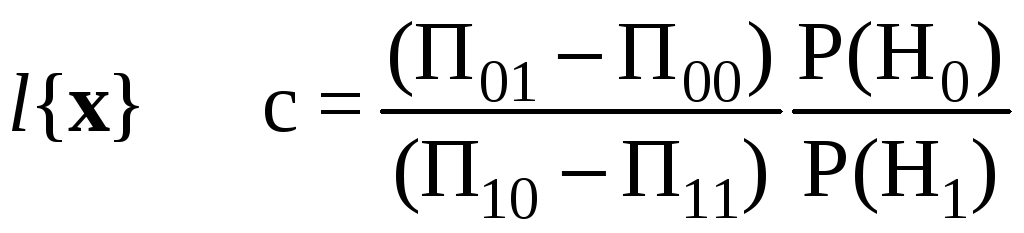, (11)

в противном случае принимается решение .

Критерий максимума правдоподобия

Для выбора оптимального критерия в системах связи может быть задана следующая матрица потерь: , ; априорные вероятности равны: . В этом случае используется критерий максима правдоподобия, который вытекает из критерия Байеса:

. (12)

Следовательно,

. (13)

2. Оптимальный приемник дискретных сигналов

Приемник дискретных сигналов принимает решение по входному сигналу, состоящему из смеси полезного сигнала и помехи , где – это сигнал, передаваемый источником сигнала (передатчиком), длительность которого ограничена в интервале . В общем случае такой сигнал можно разложить по ортогональным функциям Фурье:

; (14)

; (15)

, (16)

где ; ; ; .

Известно, что плотность распределения коэффициента любой гармоники помехи имеет гауссовское распределение с нулевым средним:

. (17)

Так как – это детерминированный процесс, то коэффициенты гармоник смеси сигнала и помехи также будут распределены по гауссовскому закону со средним значением :

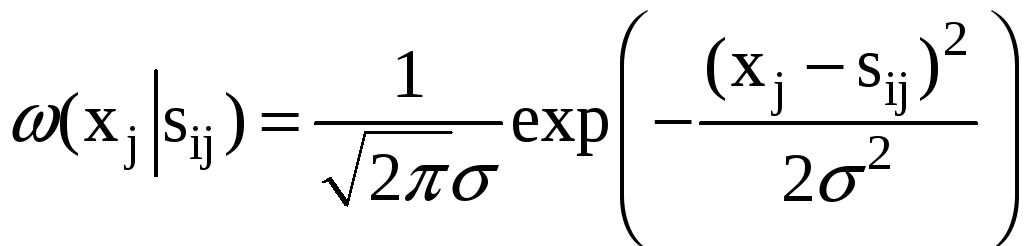. (18)

Учитывая ортогональность коэффициентов гармоник, совместная плотность распределения входного сигнала будет определяться произведением гауссовских функций:

. (19)

Рассмотрим приемник двоичных сигналов. В этом случае передаются два сигнала и . Следовательно, условные плотности распределения при приеме этих сигналов будут имеет вид:

; (20)

. (21)

Для определения принципа построения оптимального приемника воспользуемся критерием макального правдоподобия при условии равновероятной передачи каждого сигнала:

. (22)

Логарифмируя обе части неравенства, получим:

. (23)

Выполним ряд преобразований. С учетом свойств ряда Фурье:

. (24)

Произведем усреднение по времени квадрата левой и правой части выражения (24):

. (25)

В формуле (25) учтена ортогональность функций: при .

С учетом (25), условие оптимального приемника можно записать в интегральном виде:

. (26)

О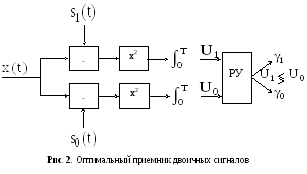 тсюда следует, что при равновероятностных сигналах оптимальный приемник воспроизводит сообщение, соответствующее тому переданному сигналу, который имеет наименьшее среднеквадратичное отклонение от принятого сигнала (рис. 2).

Откроем скобки в данных выражениях:

В случае равенства энергий сигналов условие оптимального приема преобразуется в вид

. (27)

В этом случае при условии равенства энергий сигналов приемник воспроизводит тот сигнал, взаимная корреляция которого с принятым сигналом максимальна (рис. 3).

3. Оптимальный прием с помощью согласованного фильтра

При прохождении сигнала через фильтр напряжение на его выходе определяется выражением

, (28)

где – импульсная реакция фильтра на единичный скачек напряжения на его входе .

Если взять фильтр с импульсной функцией , то выходное напряжение в момент времени

, (29)

При использовании такого фильтра прохождение через него сигнала эквивалентно вычислению взаимной корреляции с сигналом .

Для реальной реализации такого фильтра отклик должен определяться выражением

, (30)

где а и – постоянные величины.

О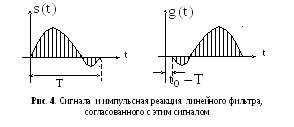 тклик такого фильтра представляет собой зеркальное отражение самого сигнала . Для реальной реализации фильтра необходимо и достаточно, чтобы при . Это условие для сигнала с ограниченным спектром выполняется при (рис. 4).

Для определения параметров такого фильтра определим его частотную характеристику путем преобразования Фурье:

(31)

При частотная характеристика фильтра имеет вид

, (32)

где – амплитудно-частотная характеристика (АЧХ) фильтра; – фазочастотная характеристика (ФЧХ) фильтра.

Для сравнения рассмотрим спектр сигнала:

,

где – амплитудно-частотный спектр сигнала; – фазочастотный спектр сигнала.

Из сравнений (31) и (32) видно, что для создания фильтра, выполняющего операцию корреляции с известным сигналом , его частотная характеристика должна быть комплексно сопряжена со спектром сигнала .

Такой фильтр принято называть согласованным фильтром, в котором АЧХ совпадает со спектром принимаемого сигнала, а его ФЧХ имеет обратный знак к фазовой характеристике сигнала. При использовании согласованных фильтров оптимальный приемник двоичных сигналов имеет вид (рис. 5).

Лекция: (4 часа) «Принципы построения систем многостанционного доступа»