6.2.2 Статические характеристики аэрационных питателей

Параметры статической (расходной) характеристики аэрациионных питателей для сыпучих материалов (в частности, УПКП), т.е. зависимости выходного расхода СМ от управляющего сигнала, должны отвечать заданным требованиям по диапазонам входного и выходного сигналов, иметь требуемый коэффициенту передачи, быть максимально приближенными к линейным, т. е, в целом, обеспечивать заданное качество регулирования в АСР. Из тех же соображений, в динамическом отношении питатель должен иметь минимальные величины инерционности и запаздывания. Следовательно, в процессе анализа и синтеза АСР необходимо, как минимум, знать параметры этих характеристик, и, желательно, уметь придать последним свойства, положительно сказывающиеся на качестве регулирования. Определение статических и динамических характеристик пневматического питателя затруднено тем, что речь идет о зависимости между управляющим давлением и расходом не сплошной, а двухфазной среды.

Математическое описание процессов перемещения двухфазных сред представляется достаточно неоднозначным, т.к. свойства такого потока зависят от многих параметров, в свою очередь, связанных между собой. Поведение направленно движущейся двухфазной смеси определяется свойствами СМ и газа-носителя, абсолютными величинами и диапазоном изменения расхода, концентрацией твердой фазы в газе, конструктивными параметрами трассы перемещения и др.

Рассмотрим работу питателя по схеме, показанной на рисунке 42.

Процесс перемещения системы «газ – сыпучее» в общем случае характеризуется следующими особенностями:

1. Частицы перемещаются не только поступательно с потоком газа, но вращаются в нем, перемещаются под углом к оси потока, сталкиваются друг с другом и со стенками трубопровода.

2. Чем меньше размеры частиц, тем больше вероятность образования в потоке агломератов частиц и газовых пузырей.

3. На параметры движения достаточно мелких частиц влияют абсолютная величина и неравномерность (пульсации) скорости несущего потока.

4. Неправильная форма частиц материала вызывает дополнительную турбулизацию несущего потока, увеличивает степень хаотичности перемещений.

5. В зависимости от концентрации частиц в единице объема смеси, их абсолютных размеров, формы и диапазона гранулометрического состава перечисленные в пунктах а) – г) явления сказываются на характере потока в большей или в меньшей степени.

1 –– емкость; 2 –– транспортный трубопровод; 3 –– аэроднище; 4 –– воздухоотделитель; 5 –– загрузочный материалопровод; 6 –– конфузор.

Рисунок 42 –– Схема управляемого пневмокамерного питателя

При возрастании давления под аэроднищем от нулевой величины, расход Q_В воздуха, прошедшего через аэроднище, увеличивается. Слой материала, находящегося между аэроднищем и входным срезом вертикального трубопровода (транспортного ствола), последовательно проходит стадии насыщения воздухом и псевдоожижения. Затем смесь твердых частиц и воздуха начинает перемещается по вертикальному трубопроводу (транспортному стволу). В зоне входа в трубопровод, образуется объем с интенсивным псевдоожижением (псевдокипением). Расход материала через ствол определяется расходом воздуха.

Статическая характеристика питателя представляет собой, в соответствии с выбранным каналом управления, зависимость расхода твердой фазы от расхода воздуха или давления в двухфазном слое на входе в транспортный ствол.

На рисунке 43 представлены результаты экспериментального определения статических характеристик УПКП при управлении расходом сухого песка при различных величинах Z [15].

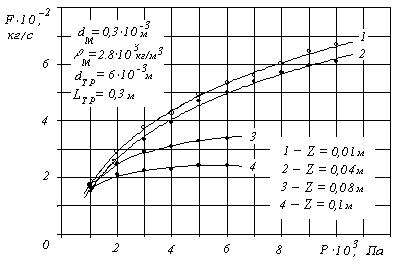
Рисунок 43 –– Статические характеристики УПКП

Точками обозначены экспериментально полученные данные. Линиям 1 и 2 отвечают соответственно, параметры Z = 0,01 и 0,04 м Статические характеристики 3 и 4 получены при Z = 0,08 и м.

Эксперимент показывает, в частности, что статические характеристики УПКП нелинейны, а коэффициент передачи устройства и, следовательно, возможный диапазон регулирования расхода СМ, существенно зависит от величины расстояния Z между аэроднищем и входным срезом транспортного ствола, т. е. от сопротивления входа в ствол. Зависимости, представленные на рисунке 43, могут быть аппроксимированы различными моделями. Существуют два подхода к описанию процесса перемещения частиц твердого в потоке газа:

• применение полуэмпирических зависимостей, аналогичных моделям непрерывных сред (континуальный подход);

• разработка и экспериментальное уточнение более полных физических моделей (в том числе дискретных и статистических), отражающих закономерности поведения отдельной частицы или потока в целом как неоднородной среды.

Применять к двухфазному потоку понятия «плотность смеси», «расход смеси», «вязкость смеси» и т.п., в общем случае не корректно. Тем не менее, если соблюдается ряд условий, а именно:

• абсолютные значение скоростей воздуха и твердого материала составляют значительную величину (десятки м/с) и разница между ними (проскальзывание) достаточно мала;

• перемещение происходит при низкой концентрации твердой фазы (истинная объемная концентрация твердого вещества в двухфазном потоке s_V < 0,04 м³/м³ [13]);

• скорость направленного перемещения частиц настолько высока, что составляющая перемещения поперек и под углами к оси потока несущественна, поток двухфазной смеси с определенной степенью приближения можно рассматривать как однородную (континуальную) среду (иначе — дисперсоид). Такой режим движения двухфазной смеси характерен для многих промышленных пневмотранспортных систем [14, 15].

В рассматриваемом устройстве при определенном выборе режима подачи газа-носителя и соответствующих характеристиках транспортируемого материала перечисленные выше условия можно обеспечить.

Уравнение для расчета потерь давления на транспортирование в этом случае может быть записано в следующем виде:

(44)

В (44) — давление в слое смеси материала с воздухом перед входом в вертикальный транспортный трубопровод; Н/м²; ¹⁵ — коэффициент, определяемый суммарным сопротивлением трассы; — суммарная длина вертикальных и горизонтальных участков трассы транспортирования, м; — высота подъема при транспортировании, м; — диаметр и площадь сечения транспортного трубопровода, м, м²; , — объемный расход и текущая плотность транспортируемой смеси, м³/с, кг/м²; — массовая расходная концентрация, кг/кг; — ускорение свободного падения, м/с².

Аналогичное по сути уравнение для приближенного расчета потерь давления при вертикальном пневмотранспортировании с учетом порозности потока e получено в [14]. Используя принятые выше обозначения и учитывая, что , это уравнение можно записать в виде:

.

(44*)

Вторыми слагаемыми в уравнениях (44) и (44*) для устройства, показанного на рисунке 42, при малых концентрациях смеси можно пренебречь. Из (44) получим:

.

(45)

В формуле (45) — коэффициент расхода;.

Уравнение (45) представляет собой статическую (рабочую, расходную) характеристику УПКП как исполнительного устройства АСР.

Для определения расхода воздуха, обеспечивающего устойчивое перемещение материала с известными характеристиками частиц, воспользуемся понятием о скорости витания одиночной частицы в восходящем потоке. Критерий Архимеда для частицы сферической формы определяется как

.

(46)

В формуле (46) — диаметр частицы материала и ее плотность, м, кг/м³; µ_В — плотность (кг/м³) и динамическая вязкость (Па∙с) воздуха.

Критерий Рейнольдса, записанный относительно скорости витания, связан с критерием Архимеда зависимостью

.

(47)

Следовательно, скорость витания частицы

(48)

Величину скорости начала устойчивого транспортирования можно определить по различным полуэмпитрическим зависимостям [16] или принять [13].

Минимальный необходимый для транспортирования расход воздуха составит

.

(49)

Последнее соотношение определяет фиктивный расход воздуха, что справедливо в условиях достаточно низкой концентрации твердой фазы.

Минимальный массовый расход двухфазной смеси

.

(50)

Величина расхода материала на начальном участке статической характеристики может быть задана из технологических условий, рассчитана по формулам для определения максимальной транспортирующей способности потока для критической скорости воздуха (например, из[16]) или приближенно установлена по данным об эксплуатации аналогичных устройств.

Объемный расход смеси

.

(51)

Текущую плотность смеси можно выразить, как

.

(52)

Массовая расходная концентрация:

.

(53)

Для определения абсциссы первой точки расчетной статической характеристики УПКП минимальному расходу СМ необходимо поставить в соответствие потери давления, возникающие при перемещении двухфазной смеси по транспортному стволу.

При известных скоростях воздуха и материала, потери давления при транспортировании можно рассчитать как сумму потерь от трения воздуха и материала , потерь на изменение количества движения массы материала и потерь на местных сопротивлениях [13, 16]. При этом в начале трассы перемещения рассматривается т. н. разгонный участок, на котором скорость твердых частиц увеличивается от практически нулевого, и даже отрицательного, до установившегося значения. В устройствах типа УПКП длина трассы от зоны загрузки до материалоотделителя невелика и практически вся является разгонным участком. Для расчета длины разгонного участка и перепада давления на нем для пневмотранспорта предложен целый ряд зависимостей [13, 16], определяемых видом материала и характеристиками трассы. Для определения длины разгонного участка применима формула:

.

(54)

В (54) и –– значение скорости материала в начале и в конце разгонного участка соответственно, м/с.

Скорость материала в конце разгонного участка принимается равной скорости установившегося движения, которая может быть рассчитана по формуле:

.

(55)

Потери давления на разгонном участке, Па:

,

(56)

где для вертикального перемещения .

Расчет потерь на местных сопротивлениях ведется по известной формуле:

.

(57)

Значения коэффициентов местных сопротивлений рассчитываются [17] или определяются по справочным данным, например, [18].

Можно определить коэффициент расхода :

(58)

В достаточно узком диапазоне регулирования расхода отношение можно считать постоянным. Если, при высоких скоростях потока уменьшением сопротивления трассы с увеличением скорости пренебречь, то приближенный расчет статической характеристики можно свести к подстановке в (45) значений управляющего давления, рассчитанных при скоростях воздуха, больших критической. В результате определяются значения массового расхода двухфазной смеси. Расход материала определится из формулы (50).

Приближенный расчет зависимости расхода материала от скорости несущего воздуха можно осуществить не переходя к формуле (45). В достаточно узком диапазоне изменения расхода истинная массовая концентрация твердой фазы в объеме трубопровода также может учитываться как постоянная величина:

.

(59)

Определив величину (кг/м³) при критической скорости воздуха, значения расхода материала при соответствующих значениях управляющего давлениях определится из формулы :

.

(60)

Здесь –– скорость воздуха в м/с, соответствующая управляющему давлению , Па; i –– число рассчитываемых точек статической характеристики.

При расчете пневмотранспортных систем широко применяется уравнение Гастерштадта [13, 14, 16,]:

.

(61)

Здесь –– суммарные потери при перемещении несущего воздуха, Па; m –– массовая расходная концентрация, кг/кг; k –– коэффициент Гастерштадта. Величина коэффициента определяется параметрами движущихся фаз, видом (вертикальный или горизонтальный) и диаметром трубопровода.

Имея в виду статическую характеристику УПКП, уравнение (61) следует записать в виде:

.

(62)

Для расчета статических характеристик аэрационных питателей может быть использована также система уравнений, аналогичных приведенным в [16] для гранул резины и каучука:

(63)

Входящие в зависимости (45) и (60)–(63) параметры — коэффициент расхода , коэффициенты и ; коэффициент Гастерштадта k и другие; плотность смеси и массовая расходная концентрация — функционально связаны между собой и с величиной расхода. Вид и параметры уравнений, описывающих эти связи, определяются свойствами твердой фазы, газа-носителя, направлением перемещения, соотношением между размерами частиц и проходным сечением трубопровода, их абсолютными величинами, а также конструкцией трассы. Поскольку эти зависимости известны далеко не во всех практических случаях, приведенные выше методики расчета характеристик пневмопитателей являются приближенными.

Параметры двухфазного потока достаточно уверенно можно рассчитать лишь для скоростей воздуха, близких к критической. В этих условиях расход воздуха минимален, а скорость твердой фазы можно определить по формуле (55). Тогда переменный расход материала можно реализовать в виде последовательности импульсов с постоянной и известной амплитудой и переменной частотой или длительностью (см. также формулы (42) и (43) для вибропитателей, раздел 2.3.1).