5.3 Информационная схема и характеристики

вибропитателя по основным каналам управления

При применении вибрационного питателя в качестве ИУ АСР, для управления расходом СМ принципиально могут использоваться следующие параметры (рисунок 33):

• частота вибрационного сигнала ;

• амплитуда вибрационного сигнала А;

• площадь выпускного отверстия S_ОТВ;

• угол наклона стенок или днища выпускного канала .

Неконтролируемыми возмущающими воздействиями для вибрационного питателя являются:

• изменение гранулометрического состава СМ Dr_М;

• влажность твердого вещества М_M;

• колебания напряжения питающей электрической сети.

Последнее возмущение вызывает нестабильность частоты вибрационного сигнала.

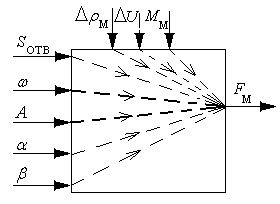
Рисунок 33 — Информационная схема вибропитателя

Изменение угловых параметров питателя технически достаточно сложно осуществимо, а управление площадью выпускного отверстия не эффективно по соображениям, приведенным в разделе 4.2. Производительностью вибропитателей с электромагнитным приводом управляют методом амплитудно-импульсной модуляции (АИМ) вибросигнала.

Рассмотрим статические характеристики вибрационных питателей, связывающие выходной расход СМ с амплитудой и частотой вибрации. Математическое моделирование механики совместного и раздельного движения массы СМ и питателя является достаточно сложной задачей. Один из методов ее решения состоит в описании движения единичной частицы с последующим обобщением на совокупность частиц с применением эмпирических коэффициентов.

В литературе приводится целый ряд методик приближенного определения среднего расхода СМ при его движении под действием вибрации [1, 7, 11, 12, 23 и др.]

При расчете вибрационных и качающихся питателей (конвейеров) в рассмотрение вводится безразмерный коэффициент l [23], отражающий связь между амплитудой колебаний А, частотой w, углом наклона желоба питателя к горизонту a и углом b между плоскостью несущей поверхности желоба и направлением вектора вибрационной силы (рисунок 34).

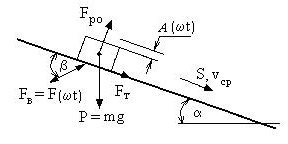
F_B — вибрационная сила; F_РО — реакция опоры; F_Т — сила трения;

А (t) — пределы изменения амплитуды вибрации; S, v_CP — направление и средняя скорость транспортирования.

Рисунок 34 — К расчету скорости перемещения материала

по вибрирующей поверхности.

.

(36)

Здесь — момент отрыва частицы от несущей поверхности.

Для вибрационного перемещения с одним подбрасыванием за период колебаний

Средняя скорость перемещения слоя СМ вибрационным питателем может быть определена по формуле В. А. Баумана:

(37)

Знак (–) применяется при подаче под углом вверх к горизонту. Величина коэффициентов и зависит от гранулометрического состава СМ. Значения коэффициентов в уравнении Баумана приведены в таблице В1 Приложения В.

Объемный расход СМ при вибрационной подаче определяется как

(38)

S_М — площадь сечения потока СМ, м²;  — коэффициент заполнения объема желоба. Для открытых желобов и прямоугольных труб  =0,6 – 0,9; для круглых труб  =0,5 – 0,6. Меньшие значения  выбираются для мелкодисперсных материалов.

Массовый расход можно рассчитать по формуле

.

(39)

Подставив (37) в (39), получим упрощенную статическую характеристику вибрационного питателя при транспортировании одним подбрасыванием за период:

.

(40)

Согласно модели (40), расход СМ линейно зависит от амплитуды при постоянной частоте, и от частоты при постоянной амплитуде вибрации. Погрешность расчета в данном случае определяется наличием эмпирических коэффициентов, а также тем, что вибрационная плотность изменяется с изменением параметров вибрации.

Для расчета горизонтальных и имеющих небольшой уклон питателей применима также зависимость для определения скорости перемещения СМ из [12]:

(41)

В формуле (41) — коэффициент, зависящий от степени передачи скорости от несущей поверхности к материалу; — коэффициент, учитывающий толщину слоя СМ; — коэффициент, зависящий от угла  наклона несущей поверхности к горизонту. Значения коэффициентов приведены в Приложении В (таблицы В2 и В3).

Пример расчета статической характеристики вибрационного ИУ для СМ приведен в Приложении Г.

В динамическом отношении вибрационные питатели по каналам «амплитуда вибрации – расход СМ» и «частота вибрации – расход СМ» представляют собой безынерционные звенья и не имеют запаздывания.

Управление виброприводом может быть реализовано в виде пакетов вибрационных колебаний, имеющих постоянную частоту и амплитуду (рисунок 35). Если в соответствии с заданной величиной среднего расхода СМ при постоянном периоде следования изменяется длительность импульсных пакетов, то реализуется принцип широтно-импульсного управления (рисунок 35а). При частотно-импульсном управлении число импульсов в пакете постоянно, а частота подачи пакетов изменяется (рисунок 35б).

Величина среднего расхода за промежуток времени t – t₀ для широтно-импульсной системы может быть определена как

.

(42)

В (42) — длительность i – го импульса расхода СМ.

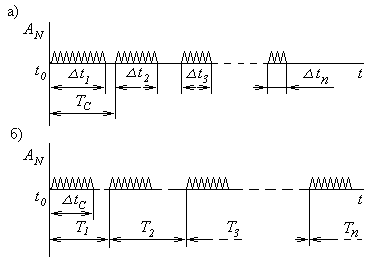
а) — широтно-импульсная модуляция (ШИМ);

б) — частотно-импульсная модуляция (ЧИМ)

Рисунок 35 — Варианты импульсного управления

вибрационным сигналом

При частотно-импульсном управлении

(43)

Здесь – постоянная длительность импульсов; n – число импульсов за рассматриваемый промежуток времени работы питателя t – t_{0 ;}

f – частота следования импульсов.

Вибрационно-импульсное управление позволяет обеспечить больший диапазон расхода СМ, чем непрерывное вибрационное. В этом случае параметры вибрации (А и ) могут быть выбраны постоянными и оптимальными с точки зрения воздействия на конкретный материал. Кроме того, импульсный метод формирования управляющего воздействия обеспечивает повышение качества регулирования на объектах с чистым запаздыванием [24].

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1. В чем особенности вибрации по сравнению с другими видами механического движения?

2. Перечислите преимущества и недостатки вибрационных устройств.

3. Какой участок статической характеристики вибропитателей следует использовать для управления расходом СМ?

4. Какие параметры вибрационных питателей можно использовать для управления расходом СМ?

5. Какие методы формирования управляющего сигнала применяются при управлении расходом СМ при помощи вибрационных питателей?

6. В чем преимущества импульсного управления расходом СМ?