Параллактический треугольник

Параллактический треугольник – сферический треугольник с вершинами P_n, Z,  (рис. 1.11). Он образован пересечением трех больших кругов: небесного меридиана, круга склонения и вертикала светила.

У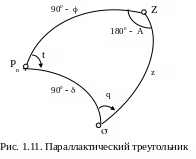 гол q между вертикалом светила и кругом склонения называется параллактическим.

Элементы параллактического треугольника относятся к трем системам координат: горизонтальной (А, z), первой экваториальной (, t) и географической (). Связь между этими системами координат может быть установлена через решение параллактического треугольника. Одна из задач, связанных с решением параллактического треугольника, формулируется следующим образом.

Дано: в момент звездного времени s в пункте с известной широтой  наблюдается светило  с известными экваториальными координатами  и .

Требуется вычислить: горизонтальные координаты светила, то есть азимут A и зенитное расстояние z.

Решение задачи выполняется по формулам сферической тригонометрии (см. прил. 1). Формулы косинусов, синусов и пяти элементов применительно к параллактическому треугольнику записываются следующим образом:

cos z = sin sin + cos cos cos t; (1.1)

sin z sin(180^о  A) = sin(90^о  ) sin t; (1.2)

sin z cos(180^о  A) = sin(90^о  ) cos(90^о  )  cos(90^о  ) sin(90^о  )cost, (1.3)

где t = s   .

Разделив формулу (1.3) на (1.2), получим:

сtg A = sin  ctg t  tg  cos  cosec t. (1.4)

Формулы (1.1) и (1.4) используются в геодезической астрономии при составлении эфемерид светил (таблиц горизонтальных координат, где аргументом служит время), а также являются уравнениями связи в зенитальных и азимутальных способах астрономических определений.

Контрольная работа № 1

1. Для заданного пункта на дату наблюдения вычислить горизонтальные координаты звезды на момент декретного времени с контролем вычислений.

Варианты:

N	K	Экваториальные координаты		Географические координаты		Дата	Декретное время
						d	Dn
1 – 31	N	5h (K)m (20+K)s	(20+K)о (K) 25	(10+K)о (10+K) 40	3h (15+K)m (K)s	(K) июля	7h (K)m (K)s
32 – 62	N – 31	9h (K)m (10+K)s	(-20-K)о (K) 25	(20+K)о (10+K) 40	5h (K)m (K)s	(K) декабря	12h (20+K)m (K)s
63 – 92	N –62	14h (K)m (20+K)s	(30K)о (K) 25	(30+K)о (10+K) 40	7h (20+K)m (K)s	(K) апреля	2h (K)m (K)s
93 – 100	N – 92	20h (K)m (10+K)s	(60+K)о (K) 25	(40+K)о (10+K) 40	9h (K)m (K)s	(K) февраля	18h (20+K)m (K)s

Примечания к вариантам: N – последние две цифры номера зачетной книжки. Пример выбора исходных данных. Если N = 70, то К = N – 62 = 8. Из таблицы получаем:

 = 14^h (K)^m (20 + K)^s= 14^h 8^m 28^s;

 = (30  K)^о (K) 25 = 22^о 8 25;

 = (30 + K)^о (10 + K) 40 = 38^о 18 40;

 = 7^h (20 + K)^m (K)^s = 7^h 28^m 8^s;

d = (K) апреля = 8 апреля;

Dn = 2^h (K)^m (K)^s = 2^h 8^m 8^s.