
- •§41. Уравнения Максвелла для квазистационарного электромагнитного поля.
- •§42. Условия квазистационарности поля.
- •§43. Глубина проникновения квазистационарного электромагнитного поля.
- •§44. Функция Грина уравнения Гельмгольца.
- •§45. Уравнения Максвелла электромагнитных волн в вакууме.
- •§46. Волновое уравнение в случае вакуума.
- •§47. Решение волнового уравнения в случае плоской электромагнитной волны в вакууме.
- •§48. Плоская монохроматическая волна.
- •§49. Уравнения Максвелла в случае плоской монохроматической волны в вакууме.
- •§50. Разложение электромагнитных полей по плоским монохроматическим волнам.
- •§51. Калибровка Лоренца в случае однородной изотропной среды.
- •Задачи по курсу «Теоретическая механика и теория поля»
- •Задачи по курсу «Теоретическая механика и теория поля» и их решение.
- •Экзаменационные вопросы по курсу «Теоретическая механика и теория поля».
- •Уравнения Максвелла для квазистационарного электромагнитного поля .
- •Задачи по курсу «Теоретическая механика и теория поля» и их решение (от а.Е.Широкова)
§41. Уравнения Максвелла для квазистационарного электромагнитного поля.
Уравнения Максвелла в среде:
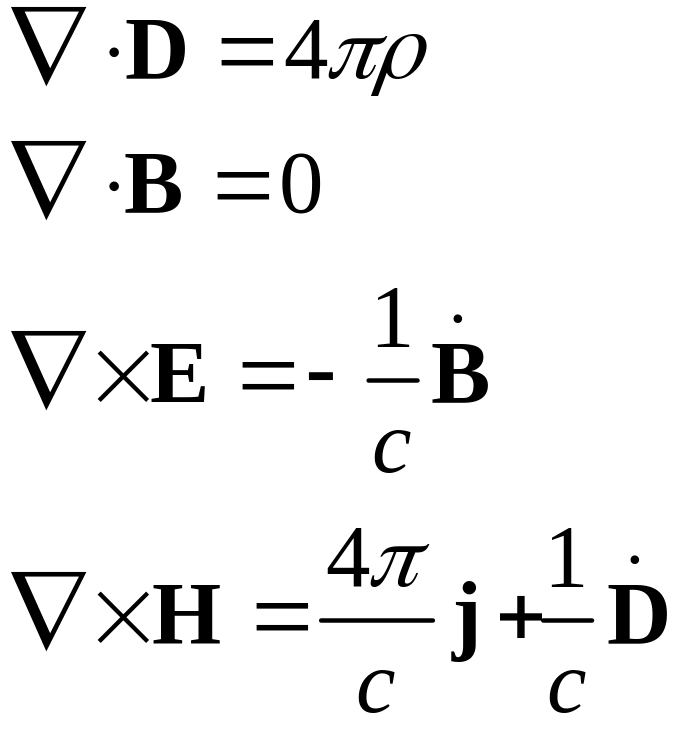
Уравнения связи для однородной изотропной среды:
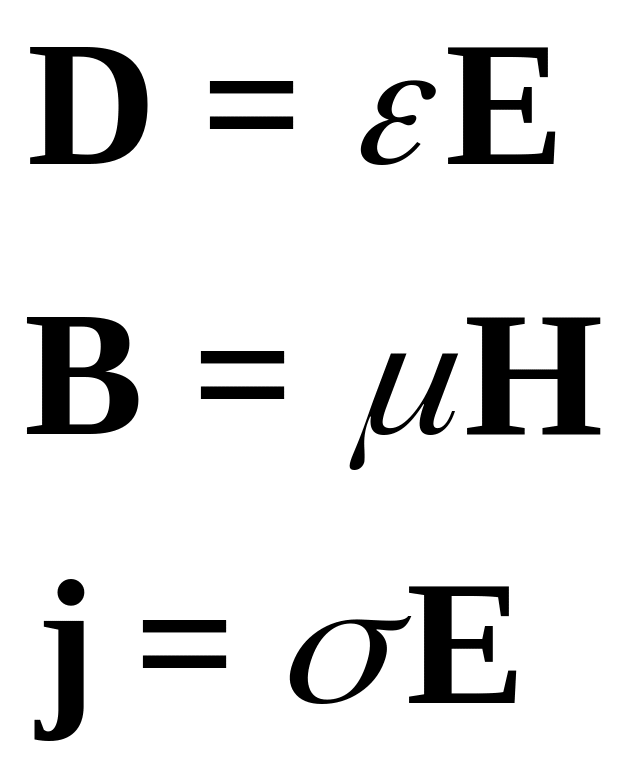
Будем рассматривать не магнитные
материалы, т.е.
![]() .
.
Случай квазистационарных полей означает, что поля считаем в одних случаях стационарными, а в других случаях – не стационарными. Для квазистационарных полей:
1)![]() ,
а
,
а
![]() отбрасываем, т.к.
отбрасываем, т.к.
![]()
2)![]() - оставляем как есть.
- оставляем как есть.
Критерий «отбрасываемости»:
Если
![]() ,
то
,
то
![]() .
Слагаемое
.
Слагаемое
![]() .
В гауссовой системе единиц
.
В гауссовой системе единиц
![]() имеет размерность как
имеет размерность как
![]() .
.
Составим отношение для сравниваемых слагаемых:
![]()
![]()
Это есть критерий или условие квазистационарности. И тогда:
Рассмотрим как упрощается
![]() :
:
![]()
Запишем закон сохранения заряда в форме уравнения непрерывности:
![]()
![]() ,
,
![]()
![]()
Используем (*), тогда:
![]()
![]() ,
где
,
где
![]()
Частное решение этого уравнения:![]()
Для проводников с высокой проводимостью
![]() мала,
мала,
![]() ,
где
,
где
![]() - период, тогда:
- период, тогда:
![]()
Но поле может и не меняться по гармоническому закону, а может меняться как угодно, тогда - время, за которое поле меняется существенно.
![]()
Тогда
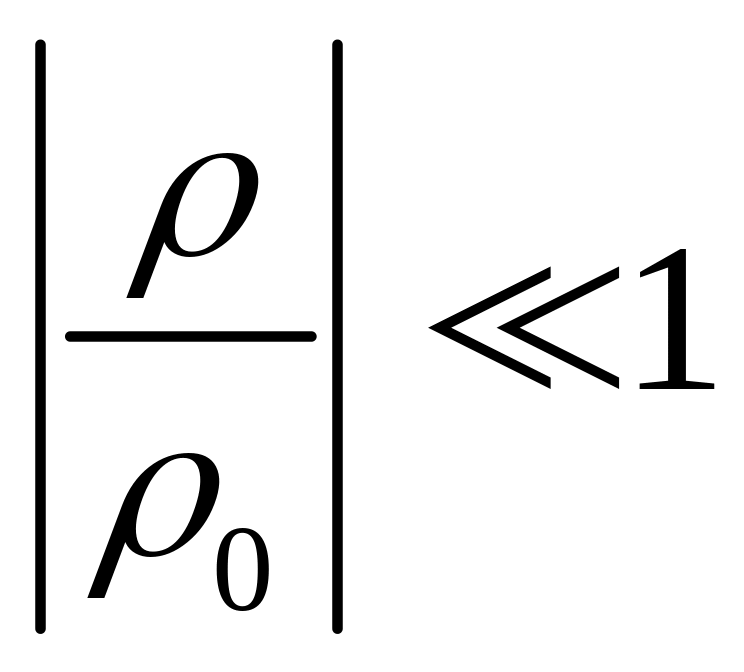 ,
и
,
и
![]()
Т.е. заряды быстро рассасываются. Значит для квазистационарного случая
![]()
В итоге получаем для квазистационарного случая систему уравнений Максвелла:

В квазистационарных полях есть эффекты:
1)Скин-эффект – быстропеременное поле вытесняет на поверхность проводника заряды.
2)Токи Фуко – переменное магнитное поле создаёт электрическое поле.
§42. Условия квазистационарности поля.
1) Мы уже рассмотрели:
2) Характерные параметры линейного
проводника
![]() характерных параметров поля
характерных параметров поля
![]() .
.
- расстояние, на котором поле существенно меняется за время (если пускаем волну, то - длина волны; если изменение поля гармоническое, то - период).
3) Если длина пробега носителя тока –
электрона
![]() ,
то она гораздо меньше параметра поля
,
т.е.
,
то она гораздо меньше параметра поля
,
т.е.
![]() .
.
4) Если носителями тока являются
перемещающиеся электроны, то вводим
характеристику
![]() ,
где
- длина пробега электрона, а
,
где
- длина пробега электрона, а
![]() -
его скорость. Тогда:
-
его скорость. Тогда:
![]()
3) и 4) позволяют записывать закон Ома без учёта пространственно-временной дисперсии, в простой форме: .
§43. Глубина проникновения квазистационарного электромагнитного поля.
Уравнения Максвелла в случае квазистационарности:
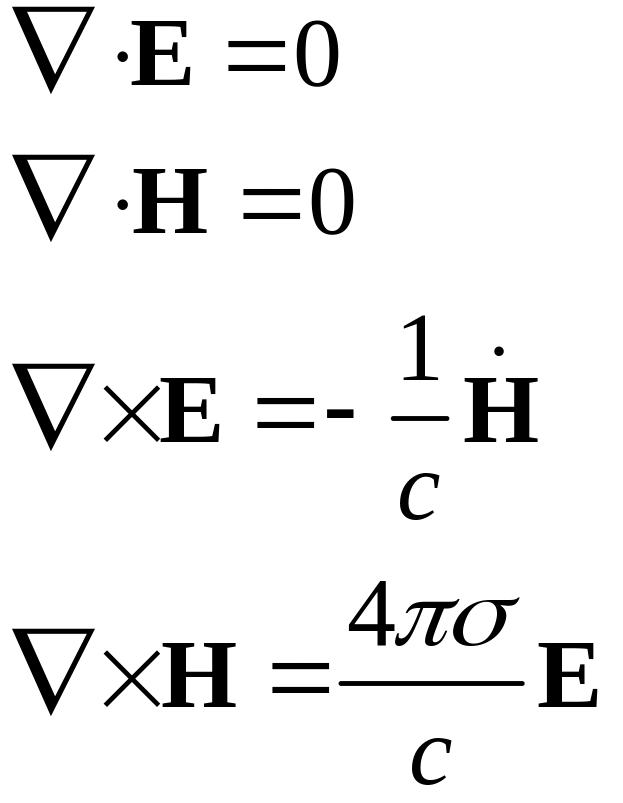
Здесь учтено, что
и
![]() .
.
На два последних уравнения Максвелла
подействуем
![]() :
:
![]()
![]() - уравнение квазистационарного поля
- уравнение квазистационарного поля
![]()
Аналогично получаем для
![]() :
:
![]()
Пусть
![]() ;
;
![]() ,
тогда:
,
тогда:
![]()
![]()
где
![]()
Размерность
![]()
![]()
 - параметр глубины проникновения поля
.
Мы получили уравнение Гельмгольца:
- параметр глубины проникновения поля
.
Мы получили уравнение Гельмгольца:
![]()
Вид решения для
зависит от формы области, где ищется
решение. Если ищем в полуплоскости, то
![]()
![]() - если взять
- если взять
![]()
тогда получим
![]() .
Это даёт граничное условие
.
Это даёт граничное условие
![]()
Если взять
![]() ,
то это даст граничное условие
,
то это даст граничное условие
![]() ,
не объясняется ни физически, ни
подтверждается экспериментально. Таким
образом, следует брать
,
не объясняется ни физически, ни
подтверждается экспериментально. Таким
образом, следует брать
![]()
![]() -параметр:
-параметр:![]()
Для поля аналогично:
![]()
![]() - решение для полупространства.
- решение для полупространства.
Будем учитывать проникновение полей и только на глубину , т.к. дальше их проникновение мало и его можно не учитывать, хотя оно существует.
