
- •Енергозберігаючі технології
- •Затверджено
- •ВСтуп…………………………………………..………5
- •Основні визначення термодинаміки……………………..6
- •2. Перший закон термодинаміки……………………………16
- •3. Другий закон термодинаміки…………………..…………30
- •1. Основні визначення термодинаміки
- •1.1. Методи термодинамічного аналізу довкілля
- •Механічна робота l виконується в тому випадку, коли на тіло масою m діє сила f на проміжку шляху s з прискоренням а:
- •Параметри стану
- •1.3. Поняття про термодинамічні процеси
- •1.3.1. Рівноважні та нерівноважні процеси
- •1.3.2. Оборотні та необоротні процеси
- •1.4. Поняття про ідеальний газ та його основні закони
- •Д (1.2) е н.У.: температура 0c або 273 к; тиск 760 мм рт. Ст. Або 101325 Па;
- •2. Перший закон термодинаміки
- •2.1. Закон збереження та перетворення енергії
- •Зовнішня робота процесу та внутрішня енергія (робочого тіла чи тдс)
- •З . Відки зовнішня робота при кінцевій зміні обєму дорівнює:
- •Внутрішня енергія
- •2.3. Рівняння і-го закону термодинаміки для робочого тіла, яке знаходиться у відносному спокої (закрита система)
- •2.4. Ентальпія
- •2.5. Теплоємність
- •2.6. Формула Майора
- •3. Другий закон термодинаміки
- •3.1. Кругові процеси (цикли). Робота та тепло кругових процесів
- •3.2. Термічний коефіцієнт корисної дії (к. К. Д.) циклу
- •3.3. Поняття про джерела теплоти
- •3.4. Формулювання іі-го закону термодинаміки
- •Загальне формулювання іі-го закону термодинаміки:
- •3.5. Поняття про прямі та обернені цикли
- •3.5.1. Прямі цикли
- •3.5.2. Обернені цикли
- •3.6. Цикли Карно. Теорема Карно
- •3.6.1. Прямий оборотний цикл Карно
- •3.6.2. Обернений оборотний цикл Карно
- •Отже, до робочого тіла від якоїсь машини підводять роботу lстиснзовн.
- •3.6.3. Термічний та холодильний коефіцієнти циклів Карно (прямих оборотних і необоротних)
- •3.7. Ентропія
- •Література
- •Навчальне видання
- •Енергозберігаючі технології
3.6.3. Термічний та холодильний коефіцієнти циклів Карно (прямих оборотних і необоротних)
Розглянемо термічний ККД циклу Карно. Ми вже знаємо, що термічний ККД довільного циклу визначається співвідношенням
ηт. =(q1 – q2)/q1,
тут q1 = T1∆s та q2 = T2∆s, але q1 > q2 та T1 > T2
тоді можна записати для циклу Карно
(3.32)
ηт.к. = (TI∆s - T2∆s)/TI∆s = (TI - T2)/TI .
Отже, для циклу Карно термічний коефіцієнт корисної дії буде максимальним, тобто
ηт.к = ηт.max = 1 – (Т2/Т1),
так як T2 ≠ 0, то T2/TI = 0 і тому ηт.к ≠ 1.
Термічний ККД циклу Карно перетворюється в одиницю в двох практично недосяжних випадках: або коли TI = ∞, або коли T2 = 0
Порівняємо тепер величини термічних ккд оборотного та необоротного циклів Карно з ідеальним газом, які здійснюються між одними і тими ж джерелами теплоти, що мають температури ТХДТ і ТГДТ. У відповідності з цим очевидно, що для підрахунку ηт оборотного циклу Карно, ми повинні у рівняння (3.32) замість величин Т1 і Т2 підставити відповідно рівні їм (з точністю до нескінченно малої величини) значення ТХДТ і ТГДТ:
![]() ,
(3.33)
,
(3.33)
де
![]() -
термічний ккд
оборотного
циклу Карно.
-
термічний ккд
оборотного
циклу Карно.
Для необоротних процесів різниця між температурами джерел теплоти і робочого тіла мають кінцеве конкретне значення:
(3.34)
TI = Т гдт - ∆TI ,
(3.35)
T2 = Тхдт + ∆ T2 ,
В цьому випадку робочий інтервал циклу звужується, оскільки TI < Тгдт, T2 > Тхдт. Із врахуванням цих співвідношень отримаємо із (3.33):
(3.36)
ηн.ц.к т.=(Тгдт - Тхдт) - (∆TI + ∆T2)/(Тгдт - ∆TI),
де ηн.ц.к т. – термічний ккд необоротного циклу Карно.
Отже
(3.37)
тобто, термічний ккд необоротного циклу Карно завжди нижчий, ніж термічний ккд оборотного циклу Карно. Зауважимо, що цей висновок отриманий нами поки що для циклу Карно, який здійснюється на ідеальному газі з постійною теплоємністю.
До аналогічного висновку можна прийти і при графічному порівнянні оборотного і необоротного процесів (рис. 3.6).
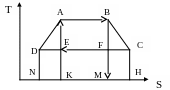
Рис. 3.6. Умовне графічне зображення прямого необоротного циклу Карно на T-s- діаграмі.
Необоротність процесу пов’язана із втратою роботи, і тому термічний ккд необоротного циклу Карно ηн.ц.кт завжди менший від оборотного ηо.ц.кт , який визначається за формулою (3.32). На рис. 3.6 умовно зображено необоротний цикл A-B-C-D-A, в якому ділянки BC і DA являють собою відповідно необоротні адіабати розширення і стиснення, які протікають із зростанням ентропії. Робоче тіло отримує від нагрівача теплоту в кількості qI = пл. A-B-M-K-A і віддає холодильнику теплоту в кількості qн2 = пл. C-D-N-Н-С. В оборотному циклі Карно - q02 = пл. F-E-K-M-F < qн2 і тому
ηо.ц.кт = 1 – (q2/q1) > ηн.ц.кт = 1 – (qн2/q1). (3.38)
Теорема Карно: термічний ккд оборотного циклу, який здійснюється між двома джерелами теплоти, не залежить від властивостей газоподібного робочого тіла, при допомозі якого цей цикл здійснюється, (але залежить від температур ХДТ та ГДТ). Таким чином, всі висновки, які були зроблені нами раніше на основі аналізу оборотного циклу Карно, який здійснюється з допомогою ідеального газу, що має постійну теплоємність, справедливі для оборотного циклу Карно з будь-яким робочим тілом. Зокрема, стосовно до будь-якого оборотного циклу Карно, справедливе отримане раніше рівняння (3.32) для термічного к. к. д. циклу можна записати у вигляді:
ηо.ц.кт = (Т1 – Т2)/Т1.
Отже, на здійснення оберненого оборотного циклу Карно була затрачена ззовні робота lц, яка еквівалентна пл. 1-2-3-4-1 (рис. 3.5а), при цьому від холодильника з температурою Тхдт отримана теплота в кількості q2 (рис. 3.5б). Для цього циклу Карно холодильний коефіцієнт розраховується за рівнянням:
ε
(3.39)
= ΔsTхдт/(ΔsTгдт - ΔsTхдт) = Tхдт/(Tгдт - Tхдт).
