- •Общие указания и примеры выполнения индивидуальных заданий
- •1.1. Задачи первой группы
- •Первая задача
- •Вторая задача
- •1.2. Задача второй группы
- •1.3. Задача третьей группы
- •Схемы для решения задач первой группы
- •Данные для решения задач второй и третьей группы
- •Схемы для решения задач второй группы
- •Тираж 500 экз. Заказ .
- •644046, Г. Омск, пр. Маркса, 35
Т. В. ВЕЛЬГОДСКАЯ, Н. В. КОВАЛЕВА, А. В. БОРОДИН
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН
О
![]()
Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
________________________
Т. В. Вельгодская, Н. В. Ковалева, А. В. Бородин
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
К ВЫПОЛНЕНИЮ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ
ПО ТЕОРИИ МЕХАНИЗМОВ И МАШИН
Утверждено редакционно-издательским советом университета
О
УДК 621.01:621.8
ББК 34.412
В28
Методические указания к выполнению индивидуальных заданий по теории механизмов и машин / Т. В. Вельгодская, Н. В. Ковалева, А. В. Бородин; Омский гос. ун-т путей сообщения. Омск, 2007. 52 с.
Методические указания содержат задания для самостоятельной работы студентов по следующим разделам курса «Теория механизмов и машин»: «Структурный анализ механизмов», «Кинематическое исследование механизмов», «Синтез зубчатых передач», приведены примеры решения задач.
Предназначены для студентов третьего курса очной формы обучения механического, теплоэнергетического и электромеханического факультетов.
Библиогр.: 4 назв. Табл. 1. Рис. 18. Прил. 4.
Рецензенты: доктор техн. наук, профессор В. В. Сыркин;
доктор техн. наук, профессор А. А. Рауба.
__________________________
© Омский гос. университет
ОГЛАВЛЕНИЕ
Введение….………………………………………………………………………. 1. Общие указания и примеры выполнения индивидуальных заданий….…... 1.1. Задачи первой группы………………….………………………………... 1.1.1. Первая задача…………………………………………………………… 1.1.2. Вторая задача…………………………………………………………… 1.2. Задача второй группы……………………………….…………………… 1.3. Задача третьей группы………………………………...………………… Библиографический список…………………………………………………….. Приложение 1. Схемы для решения задач первой группы ………................... Приложение 2. Данные для решения задач второй и третьей групп... ……… Приложение 3. Схемы для решения задач второй группы…..……………...... Приложение 4. Пример оформления титульного листа..………………........... |
5 6 6 7 10 14 15 18 19 33 45 51 |
ВВЕДЕНИЕ
В соответствии с учебными планами и программами студенты механического и теплоэнергетического факультетов выполняют курсовой проект по курсу «Теория механизмов и машин».
Для студентов электромеханического факультета курсовой проект не предусмотрен, а отведены часы для занятий в аудитории, в связи с этим разработан банк заданий. При составлении индивидуальных заданий авторы использовали схемы механизмов из различных областей техники, представляющие интерес как с точки зрения методической, так и с точки зрения возможного использования этих схем при решении практических задач. С этой целью авторы включили в задания схемы широко применяемых в технике и на железнодорожном транспорте четырех-, шести- и многозвенных механизмов в различных видах. Значительное число примеров посвящено кулачковым и зубчатым механизмам.
Индивидуальные задания содержат задачи трех групп. В данной работе приведены числовые примеры решения задач каждой группы.
Контроль качества знаний по дисциплине «Теория механизмов и машин» осуществляется по рейтинговой системе. Баллы, полученные за решение задач индивидуального задания, суммируются с баллами за выполнение лабораторных работ, знание теоретического материала (тестовые опросы в семестре), ведение конспектов и т. д.
Общие указания и примеры выполнения индивидуальных заданий
Индивидуальные задания необходимо выполнять на листах писчей бумаги формата А4 (210 × 297). Схемы к задачам рекомендуется вычерчивать на белой или миллиметровой бумаге формата А3 или А4, чертеж зубчатого зацепления – на листах формата А3 или А2. Все листы следует скрепить с титульным листом. Пример оформления титульного листа приведен в прил. 4.
Задания включают в себя задачи, разделенные на три группы в соответствии с учебной программой.
В первую группу включены две задачи, которые оцениваются пятью и десятью баллами соответственно. Задачи второй и третьей групп десятью баллами каждая.
Вариант задач для каждого студента определяет преподаватель. После выбора по варианту задания для задач второй и третьей группы (прил. 2) следует найти соответствующую схему в прил. 3.
1.1. Задачи первой группы
В первую группу включены две задачи, схемы к ним приведены в прил. 1. Схема к первой задаче содержит только низшие кинематические пары р5 пятого класса (схемы 1 84), ко второй задаче – низшие кинематические пары р5 и высшие р4 четвертого класса (схемы 85 168).
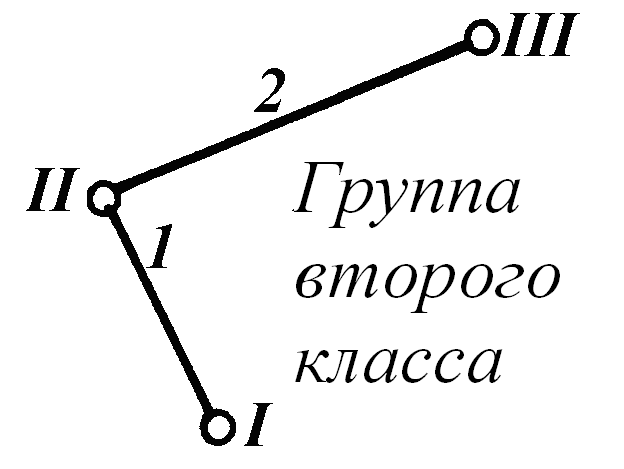
При решении задач требуется вычертить кинематические схемы механизмов без соблюдения масштаба, используя условные обозначения 1, 2; пронумеровать звенья арабскими цифрами, кинематические пары – римскими; подсчитать степень подвижности механизма, определить его класс, вычертив отдельно каждую группу Ассура с соответствующими обозначениями звеньев и кинематических пар. Степень подвижности и класс определить для двух случаев ведущего звена (на схеме в одном случае ведущее звено обозначено сплошной стрелкой, в другом – пунктирной); записать структурную формулу образования механизма (для обоих ведущих звеньев). Если при определении подвижности у механизма выделены два ведущих звена, то, составляя структурную формулу, следует учесть обозначение попарно на схеме механизма ведущих звеньев (см., например, схему 16).
Первая задача
Выбрав из прил. 1 по заданному преподавателем варианту схему механизма, приступаем к решению.
З а д а ч а 1.
Вычерчиваем кинематическую схему механизма (рис. 1.1).
Определяем степень подвижности механизма по формуле:
![]() ,
(1.1)
,
(1.1)
где 3 – степень подвижности каждого звена на плоскости;
n – общее количество звеньев, включая стойку (опору);
р5, р4 – количество кинематических пар пятого и четвертого класса;
2, 1 – количество условий связи, накладываемое кинематическими парами р5 и р4 соответственно;
3* степень подвижности стойки как самостоятельного звена на плоскости.
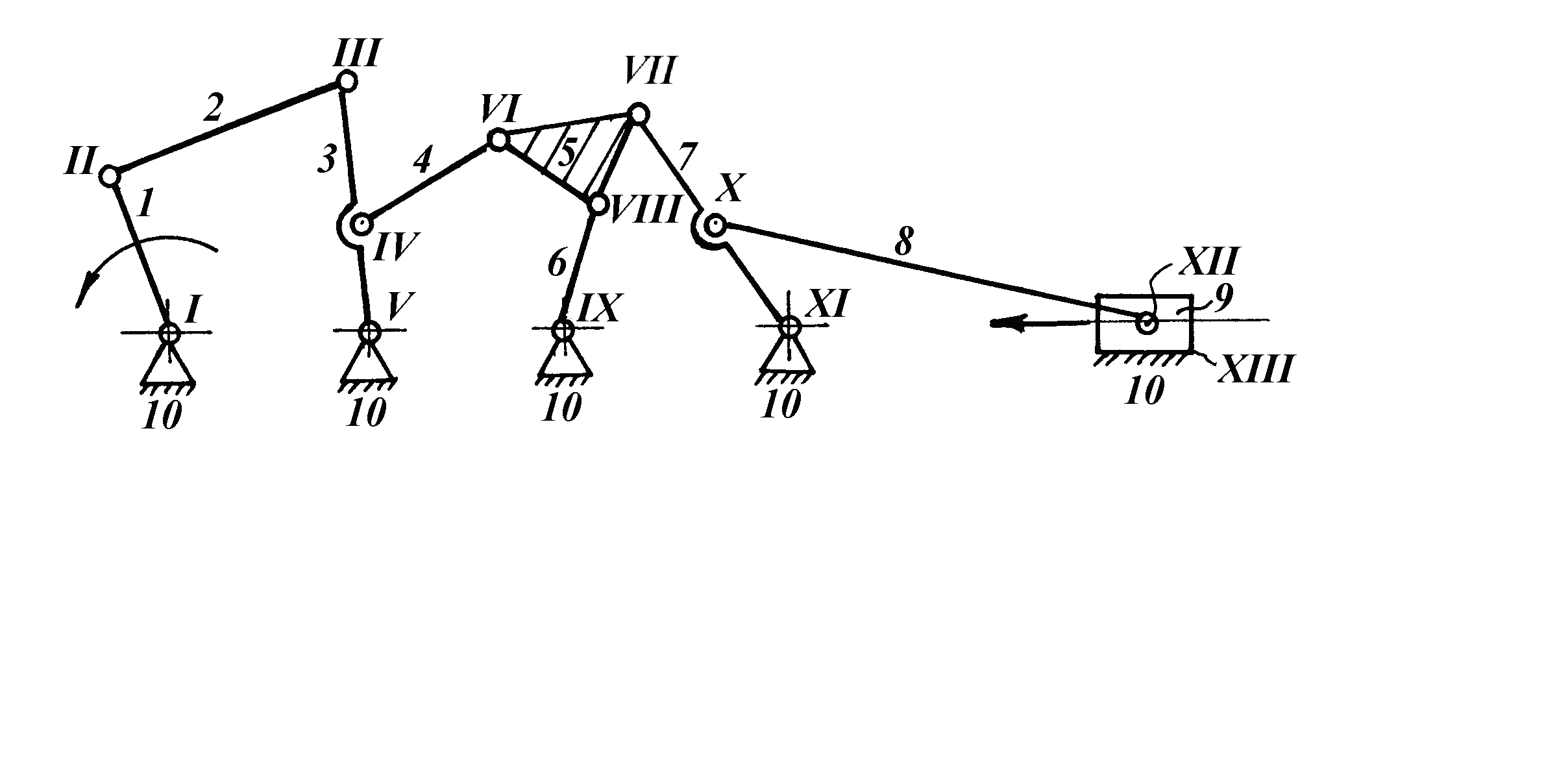
Рис. 1.1
Для механизма, приведенного на рис. 1.1, имеем:
![]()
Так как W = 1, механизм имеет в своем составе одно ведущее звено. Этим звеном может быть любое звено 1, 3, 6, 7 или 9, соединенное со стойкой. Принимаем в первом случае за ведущее звено 1 кривошип, во втором случае – звено 9 ползун.
Определяем класс механизма при ведущем звене 1:
а) отсоединяем самую удаленную от ведущего звена группу Ассура второго класса, состоящую из звеньев 9 и 8 с кинематическими парами Х, XII, XIII, и проверяем степень подвижности оставшегося |
Рис. 1.2 |
механизма, она не должна измениться в случае правильного отсоединения группы Ассура (рис. 1.2). Оставшийся механизм имеет:
![]()
![]()
б) отсоединяем группу Ассура второго класса, самую удаленную от ведущего звена. Такая группа может состоять из звеньев 7 и 5 с кинематическими парами VII, VIII, XI (рис. 1.3). При ее отсоединении механизм распался: звенья 4 и 6 не соединяются с другими звеньями. Значит, отсоединение выполнено неверно, и следует отсоединить группу более высокого класса. В рассматриваемом случае это будет группа третьего класса, состоящая из звеньев 7, 5, 6, 4 с кинематическими парами IV, VI, VIII, VII, IX, XI (рис. 1.4).
После отсоединения группы третьего класса проверяем степень подвижности оставшегося механизма:
Отсоединение выполнено верно; в) отсоединяем от оставшегося механизма группу Ассура второго класса звенья 2 и 3 с кинематическими парами II, III, V (рис. 1.5). Проверяем степень подвижности оставшегося механизма (ведущее звено 1 с кинематической парой I):
|
Рис. 1.3
Рис. 1.4
|
|
Рис. 1.5 |
Отсоединение выполнено верно; г) составляем структурную формулу образования механизма в порядке присоединения групп Ассура к ведущему звену и стойке: |
|
12; 34; 5; 6; 78; 9.
Оставшийся механизм состоит из ведущего звена, стойки, двух групп Ассура второго класса и одной группы третьего класса. Так как класс механизма определяется наивысшим классом входящих в него групп, то делаем вывод, что данный механизм является механизмом третьего класса.
Определяем класс механизма при ведущем звене 9:
а) отсоединяем самую удаленную от ведущего звена группу Ассура второго класса, состоящую из звеньев 1 и 2 с кинематическими парами I, II, III (рис. 1.6), и проверяем степень подвижности оставшегося механизма (она не должна измениться):
![]()
![]()
Отсоединение выполнено верно;
б) отсоединяем группу второго класса, состоящую из звеньев 3 и 4 с кинематическими парами IV, V, VI (рис. 1.7), и проверяем степень подвижности оставшегося механизма:
![]()
![]()
Отсоединение выполнено верно;
Рис. 1.6 |
в) отсоединяем группу Ассура второго класса, состоящую из звеньев 5 и 6 с кинематическими парами VII, VIII, IX (рис. 1.8), и проверяем степень подвижности оставшегося механизма:
|
Отсоединение выполнено верно; г) отсоединяем последнюю группу от ведущего звена, состоящую из звеньев 7 и 8 с кинематическими парами X, XI, XII (рис. 1.9), и проверяем степень подвижности оставшегося ведущего звена:
Отсоединение выполнено верно; д) составляем структурную формулу для данного механизма при ведущем ползуне 9:
98; 76; 54; 32; 1.
Данный механизм состоит из четырех групп Ассура второго класса, ведущего звена и стойки, значит, он является механизмом второго класса. |
Рис. 1.7
Рис. 1.8
Рис. 1.9 |
Вывод: класс механизма зависит от назначения ведущего звена.