Правило распространения сигналов в сети.

а) правило комбинирования входящих сигналов

Довольно часто входящие сигналы элемента предполагается комбинировать путем суммирования их взвешенных значений. Пример этого метода суммирования показан на рис. 5 , где обозначает результат комбинирования ввода элемента j, - выход элемента i, а n – число задействованных связей. Используются и другие формы комбинирования входящих сигналов, и другим часто встречающимся методом является рассмотрение квадрата разности между значением силы связи и значением передаваемого по связи сигнала с последующим суммированием таких разностей для всех входящих связей данного элемента.

Рис. 5.

или в векторном представлении

Правило вычисления сигнала активности.

Для всех элементов имеется правило вычисления выходного значения, которое предполагается передать другим элементам или во внешнюю среду. Это правило называют правилом активности, а соответствующее выходное значение называют активностью соответствующего элемента. Активность может представляться либо некоторым действительным значением произвольного вида, либо действительным значением из некоторого ограниченного интервала значений (например, из интервала [0,1]), или же некоторым значением из определенного дискретного набора значений (например, или ). На вход функции активности поступает значение комбинированного ввода данного элемента. Примеры функций активности приводятся ниже.

Тождественная функция.

Функция активности для входных элементов может быть тождественной функцией, и это просто означает, что значение (сигнал, посылаемый другим элементам) оказывается в точности равным комбинированному вводу (рис. 6). Входные элементы обычно предназначены для распределения вводимых сигналов между другими элементами сети, поэтому для входных элементов обычно требуется, чтобы исходящий от элемента сигнал был таким же, как и входной. В отличие от других элементов сети, входные элементы сети только по одному входному значению. Например, каждый входной элемент может получать сигнал от одного соответствующего ему датчика, размещенного на фюзеляже самолета. Один этот элемент связывается со многими другими элементами сети, так что данные, полученные от одного датчика, оказываются распределенными между многими элементами сети.

Рис. 6.

Пороговая функция.

В большинстве моделей НС используются нелинейные функции активности. Пороговая функция ограничивает активность значениями 1 или 0 в зависимости от значения комбинированного ввода в сравнении с некоторой пороговой величиной (рис. 7).

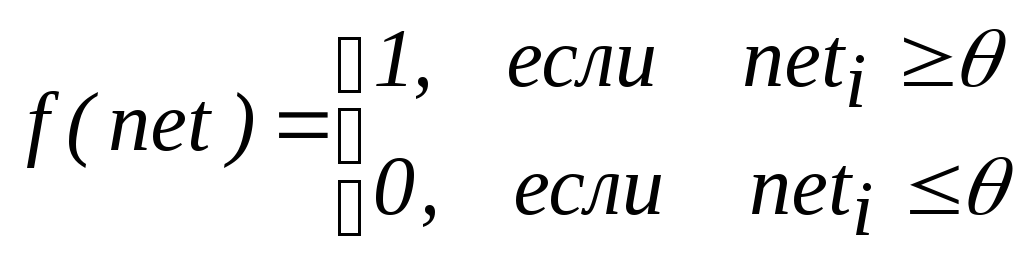
Рис. 7. Пороговая функция

Чаще всего удобнее вычесть пороговое значение (называемое смещением или сдвигом) из значения комбинированного ввода и рассмотреть пороговую функцию в ее математически эквивалентной форме, показанной на рис. 8. Сдвиг в данном случае оказывается отрицательным, а значение комбинированного ввода вычисляется по формуле

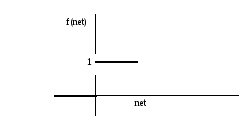
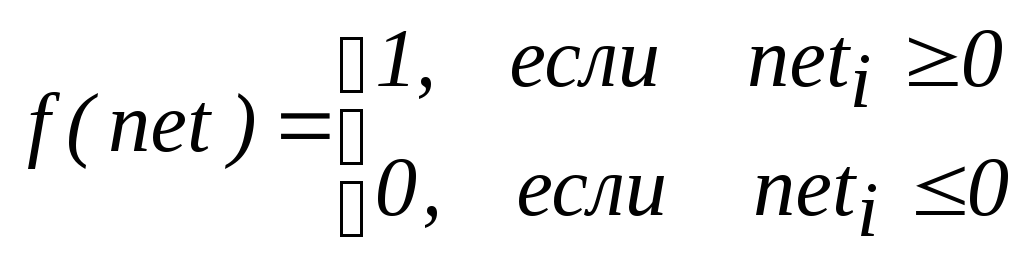
Рис. 8.

Сдвиг обычно интерпретируется как связь. Исходящая от элемента активность которого всегда равна 1. комбинированный ввод в этом случае можно представить в виде

где х₀ всегда считается равным 1.

Сигмоидальная функция.

Наиболее часто используемой функцией активности является сигмоидальная функция. Выходные значения такой функции непрерывно заполняют диапазон от 0 до 1. примером может служить логистическая функция, показанная на рис. 9.

Наклон и область выходных значений логистической функции могут быть разными. Например, для биполярного сигмоида областью выходных значений является диапазон -1 и 1.

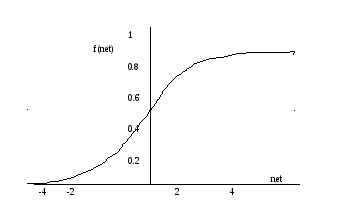
Рис. 9.

Обучение НС.

Качество работы НС сильно зависти от предъявляемого ей в процессе набора учебных данных. учебные данные должны быть типичными для задачи, решению которой обучается сеть. Обучение часто оказывается уникальным процессом, когда приемлемые решения многих проблем могут быть получены только в процессе многочисленных экспериментов. Разработчикам решения на основе нейронной сети требуется следующее.

• Выбрать соответствующую модель сети.

• Определить топологию сети (т.е. число элементов и их связи)

• Указать параметры обучения.

Существуют три парадигмы обучения: с учителем, без учителя и смешанная.