Техническая термодинамика

Под нормальными физическими условиями понимаются следующие параметры: давление 760 мм. рт. ст. и температура 0ºС.

Соотношения шкал температур: , где T – температура в градусах Цельсия, – в градусах Ренкина, – Фаренгейта, – Реамюра, – Кельвина.

Соотношения шкал давлений: .

Удельный объём , где  – плотность.

Термодинамической системой называется совокупность материальных тел, взаимодействующих как между собой, так и с окружающей средой. Если хотя бы один из параметров изменяется, то изменяется и состояние системы, т.е. осуществляется термодинамический процесс.

Типы процессов: изотермический (Бойля-Мариотта), изобарический (Гей-Люссака), изохорический (Шарля), адиабатический , политропный .

Закон Менделеева-Клапейрона: , где – количество молей вещества, m – масса газа, M –молярная масса, – универсальная газовая постоянная.

Чистое вещество – такое вещество, в котором все молекулы одинаковы.

Смесь, состоящая из нескольких чистых веществ называется раствором.

Массовая доля i-го компонента раствора , где m – масса раствора; объёмная доля , где – молярная доля i­-го компонента. . Давление смеси , где – давление i-го компонента (парциальное давление), . Кажущаяся молярная масса .

Теплоёмкость вещества – количество тепла, необходимая для нагрева его на 1 К.

Истинная теплоёмкость – теплоёмкость при данной температуре .

Удельная теплоёмкость вещества .

Средняя теплоёмкость .

, где – объёмная теплоёмкость, , где – молярная теплоёмкость, , здесь V – объём при нормальных температуре и давлении.

Внутренняя энергия и энтальпия тела как функции состояния

Внутренняя энергия тела складывается из поступательного и вращательного движения молекул, потенциальной энергии связей молекул, энергии колебаний молекул, внутриатомной и внутриядерной энергий. Внутренняя энергия обладает экстенсивным свойством, т.е. зависит от массы тела.

Энтальпия , где U – внутренняя энергия. Удельная энтальпия, соответственно, .

I закон термодинамики: или , где Q и q – обычное и удельное тепло, U и u = обычная и удельная внутренняя энергия, и – обычная и удельная работа при переходе из первого состояние во второе. В дифференциальной форме: (здесь используется символ «», т.к. тепло зависит также от способа его передачи, т.е. выражение справа не является полным дифференциалом тепла). Т.к. , то (здесь выступает в роли технической работы, т.е. работа, совершённая оборудованием).

В случае изотермического процесса теплоёмкость , изобарного: .

Другая формулировка I закона термодинамики: Энергия изолированной термодинамической системы остаётся неизменной независимо от того, какие процессы в ней протекают.

Р ассмотрим первый закон термодинамики в применении к движущемуся потоку. Для этого возьмём произвольный канал, по которому движется газ. Возьмём два сечения канала. Пусть площади их соответственно и , высота над землёй и , скорость входящего потока , выходящего , среднее по сечению давление и .

Рассмотрим изменения энергии: удельная работа проталкивания вещества сквозь канал ; изменение удельной кинетической энергии ; изменение удельной потенциальной энергии: , удельная работа трения: , удельная полезная работа: . Тогда суммарная удельная работа , изменение суммарной удельной работа и I-й закон термодинамики выглядит так: . При этом , где – тепло, получающееся за счёт трения, – внешний нагрев. Тогда . Если , то . Если процесс адиабатический ( , т.е. ), то и .

Функция является полным дифференциалом, т.е. является функцией состояния системы и называется энтропией (здесь – удельной). В случае обратимых процессов , необратимых – . Энтропия является мерой неупорядоченности системы.

. Аналогично .

Схема работы теплового двигателя

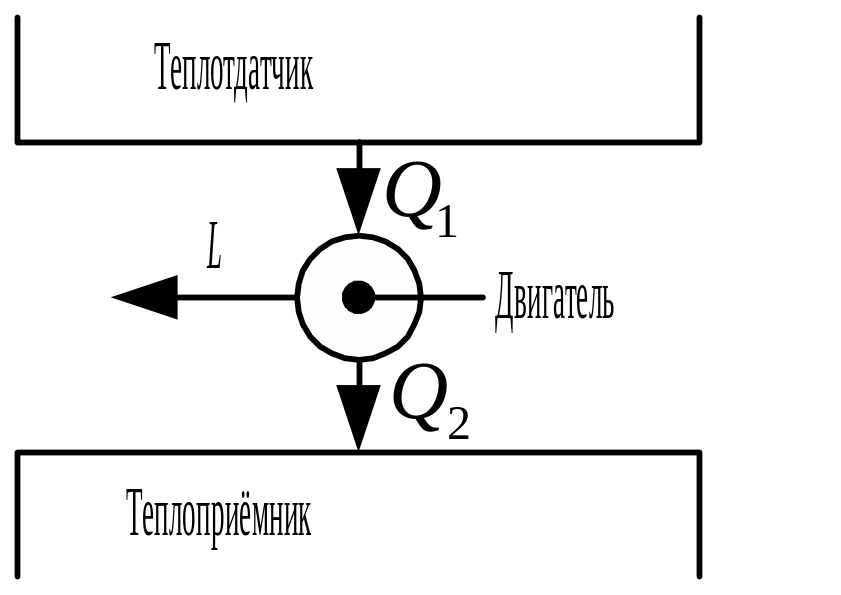
– уравнение теплового баланса в двигателях.

КПД теплового двигателя .

Пусть у теплоприёмника и теплоотдатчика поддерживаются постоянные температуры и . Рассмотрим цикл двух изотерм и двух адиабат (Цикл Карно):

.

Теорема Карно: Значение КПД для цикла Карно определяется исключительно температурами теплоотдатчика и теплоприёмника независимо от рода рабочего тела, размеров двигателя и конструктивных особенностей.

Термодинамической вероятностью называют число микросостояний, результирующих данное макросостояние.

Энтропия , где k – постоянная Больцмана, W – термодинамическая вероятность.

Изопроцессы

И зотермический процесс:

.

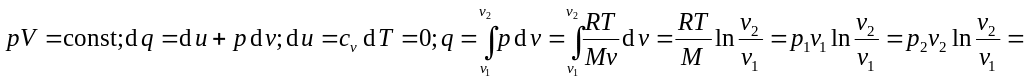
Изобарный процесс: (здесь q – техническая работа); .

Изохорный процесс: .

Адиабатический процесс: ;  в течение какого-то процесса может, вообще говоря, меняться, например, при изменении агрегатного состояния рабочего вещества (перегретый пар  насыщенный пар  обычный пар).

С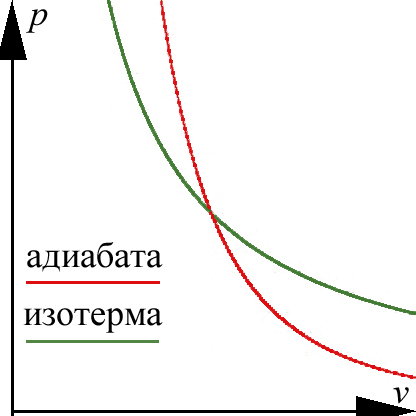 остояние системы описывается уравнениями: .

Политропный процесс: . При он переходит в изобарный процесс, при – изотермический, – адиабатический, – изохорный (здесь уравнение удобно представлять в виде ). , где .

Дифференциальные уравнения термодинамики. Основные математические методы.

Уравнения Максвелла

Первый закон термодинамики гласит, что . Пусть x и y – термодинамические параметры, т.е. . Тогда . Аналогично и для y. , . Т.к. все используемые функции у нас считаются непрерывными, то , где . Тогда, т.к. , то или . Начнём перебирать x и y. Заметим, что, например, и . В результате получаются четыре уравнения Максвелла: .

Частные производные внутренней энергии и энтальпии

(согласно одному из уравнений Максвелла) – характеризует зависимость внутренней энергии от удельного объёма в изотермическом процессе.

– зависимость энтальпии от давления в изотермическом процессе.

Обратимость и производство работы

Будем рассматривать изолированную систему с источником работы. Производство работы изолированной системой возможно в процессе перехода системы из неравновесного состояния в равновесное, причём величина работы зависит от характера процесса перехода.

Пусть – параметры окружающей среды (которая тоже входит в изолированную систему), p и T – параметры источника работы и пусть . Пусть также внутренняя энергия и объём источника работы в начале процесса есть и , в конце – и , окружающей среды в начале и , в конце – и . Тогда работа, совершённая в системе . Пусть – это количество тепла, которое источник работы передал окружающей среде, – работа, совершаема источником над окружающей средой. Тогда . Т.к. , то или . Это уравнение даёт значение полезной работы, произведённой системой при переходе из неравновесного состояния в равновесное, т.к. из всей произведённой работы вычитается та её часть, которая затрачивается на сжатие среды, а, следовательно, не может быть использована в наших целях. Однако это уравнение не даёт максимальную величину полезной работы, т.к. не обуславливает обязательной обратимости всех происходящих в системе процессов. Для нахождение максимальной полезной работы (работоспособности) можно воспользоваться тем, что при протекании обратимых процессов энтропия системы не изменяется, т.е. . Максимальная полезная работа . Удельная максимальная полезная работа называется эксергией. Обозначение: ex. . Потеря работоспособности , где – полезная работа. Также эта величина называется энергетической потерей.