Тема №6. Напряжения

Было отмечено, что в поперечном сечении стержня действуют не сосредоточенные внутренние усилия N, Q, M_k и т. д., а непре­рывно распределенные силы, интенсивность которых может быть различной в разных точках сечения и в разном направлении.

Как же измерить интенсивность внутренних сил в данной точке данного сечения, например в точке В (рис. 6.1).

Выделим вокруг точки В малую площадку A. Пусть – R равнодей­ствующая внутренних сил, действую­щих на эту площадку.

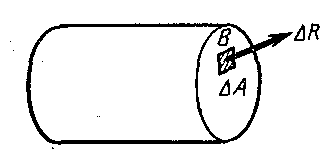
Рис. 6.1.

Тогда среднее значение внутрен­них cил, приходящихся на единицу площади рассматриваемой площадки A, будет равно

.

Величина р_ср называется средним напряжением. Она характеризует среднюю интенсивность внутренних сил. Уменьшая размеры площади, в пределе получим

p = .

Величина р называется истинным напряжением или просто напряжением в данной точке данного сечения. Упрощенно мож­но сказать, что напряжением называется внутренняя сила, при­ходящаяся на единицу площади в данной точке данного сечения.

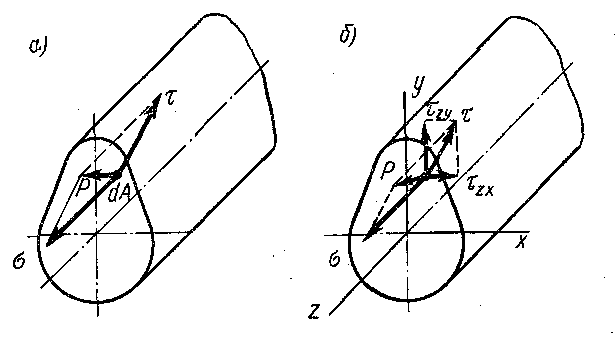
Рис. 6.2.

Полное напряжение р можно разложить на две составляю­щие (рис. 6.2, а):

1) составляющую, нормальную к плоскости сечения. Эта составляющая обозначается  и называется нормальным напря­жением;

2) составляющую, лежащую в плоскости сечения. Эта со­ставляющая обозначается  и называется касательным напря­жением. Касательное напряжение в зависимости от действую­щих сил может иметь любое направление в плоскости сечения. Для удобства  представляют в виде двух составляющих по направлению координатных осей (рис. 6.2, б).

Принятые обозначения напряжений показаны на рис. 6.2, б.

У нормального напряжения ставится индекс, указывающий, какой координатной оси параллельно данное напряжение. Растягивающее нормальное напряжение считается положительным, сжимающее – отрицательным. Обозначения касательных на­пряжений снабжены двумя индексами: первый из них указыва­ет, какой оси параллельна нормаль к площадке действия данно­го напряжения, а второй – какой оси параллельно само напря­жение.

Разложение полного напряжения на нормальное и касатель­ное имеет определенный физический смысл. Нормальное напря­жение возникает, когда частицы материала стремятся отдалить­ся друг от друга или, наоборот, сблизиться. Касательные напря­жения связаны со сдвигом частиц материала по плоскости рассматриваемого сечения.

Тема №7. Определение внутренних усилий

Рассмотрим случай осевого (центрального) растяжения или сжатия, когда внешние силы действуют по оси стержня (рис. 7.1). Для определения внутренних усилий (продольных сил) применим метод сечений.

Проведем какое-нибудь сечение, например а – а, и рассмот­рим равновесие нижней отсеченной части. Воздействие верхней отброшенной части на нижнюю заменим продольной силой и предварительно направим ее от сечения, т. е. предположим, что сила является растягивающей. Составим уравнение равнове­сия. Проецируя все силы, действующие на нижнюю часть, на направление параллельное оси стержня, и приравнивая сумму проекций нулю, получаем N₁ + 8Р – 5Р = 0, откуда N₁ = –3Р.

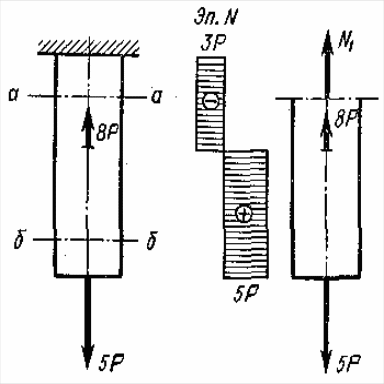
Рис. 7.1.

Знак минус показывает, что направление силы N₁ следует изменить на обратное, т. е. продольная сила будет в данном случае не растягивающей, как мы предположили, а сжимающей. Аналогично найдем продольную силу в сечении б – б: N₂ = 5Р (растяжение). Условимся продольную силу, соответствующую растяжению, считать положительной.

Наглядное представление о законе изменения продольных сил по длине стержня дает график (зпюра продольных сил), ось абсцисс которого проводится па­раллельно оси стержня, а ось ординат ей перпендикулярна. По оси ординат в выбранном мас­штабе откладывают значения про­дольных сил (с учетом знаков) в поперечных сечениях стержня. Для рассмотренного случая эпю­ра N представлена на рис. 7.1.