Лекция 5.

5.2 Уравнения движения ла в скалярной форме

В практических исследованиях векторные уравнения (5.2), (5.3) заменяют эквивалентной системой дифференциальных уравнений в проекциях на выбранные (обычно связанные с центром масс ЦМ ЛА) системы координат.

Будем считать, что путем параллельного переноса силы приложены в ЦМ ЛА. Если вектор силы направлен от нас, обозначим , а в случае - к нам будем обозначать .

Рассмотрим схему действующих сил для 3-х видов ЛА (рис.21).

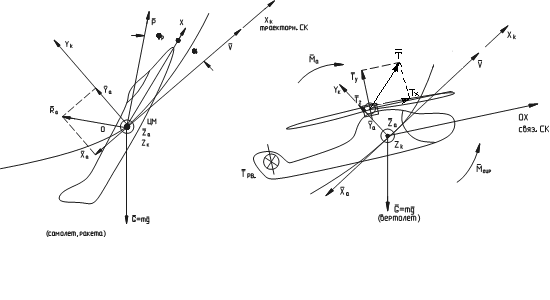
Рис. 21

р – угол установки двигателя, угол поворота по отношению к связанной СК

- полный вектор тяги несущего винта, ( –компоненты в связанной СК), –гироскопический момент от вращающихся частей (винты, ротор) – тяга рулевого винта

Уравнения движения ЦМ самолетов и ракет и их вращательное движение в инерциальной системе отсчета в векторной форме (5.2),(5.3) c учетом действующих сил и моментов запишем в виде:

m ; (уравнение сил) (5.4)

. (уравнение моментов) (5.5)

Если система отсчета неинерциальная, то добавляются кориолисовы и переносные силы инерции. Для большинства ЛА и - малы. Индекс “0” в выражениях для и здесь и в дальнейшем будет опускаться. , т.к. обычно выбранные системы координат располагаются в ЦМ ЛА.

Уравнения движения вертолета

m ;

(уравнение сил) (5.6)

.

(уравнение моментов) (5.7)

Наиболее простую форму система уравнений движения ЦМ самолетов и ракет примет, если (5.4) спроецировать на оси траекторной системы координат .Получим уравнения движения относительно сферической невращающейся Земли при отсутствии ветра ([1], стр.29).

; (5.8)

; (5.9)

(5.10)

Составляющие ;

представляют собой центробежные силы инерции, обусловленные кривизной земной поверхности. Здесь - угол местной широты. Если Землю считать плоской т.е. ,то этими составляющими пренебрегают. Ускорение, обусловленное кривизной Земли при скорости ЛА около 1000 достигает 1,6 от g(H). Для ЛА, у которых скорость кривизна Земли обычно не учитывается, или учитывается в виде поправок в конечные результаты расчетов.

В уравнения (5.8) – (5.10) входит масса самолета или ракеты, которая меняется с течением времени из-за выгорания топлива, поэтому рассматривается дополнительное дифференциальное уравнение для учета изменения массы ЛА.

(5.11)

где – секундный массовый расход топлива;

– степень дросселирования тяги двигателя.

Проецирование векторных уравнений на выбранные СК удобно производить с помощью таблиц (матриц) направляющих косинусов между различными СК [1], [2] и использовать матричные преобразования (см.Приложение 1,таблица 1,2.).

Тот же результат можно получить, если использовать «теорию бесконечно малых величин» для описания изменения параметров траектории.

Например: (Земля принимается плоской) (рис. 22).

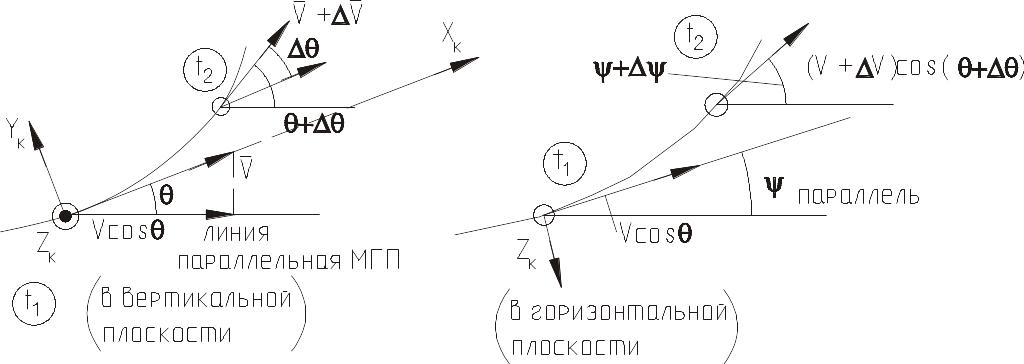
Рис. 22

Здесь t₂=t₁+t, OX_k совпадает с . Поэтому проекция ускорения на OX_k будет равна:

Проекция на OY_k:

.

Проекция на OZ_k:

У нас . Аналогично можно вывести проекции сил и ускорений, обусловленных кривизной Земли.

Рассмотрим уравнения моментов в скалярной форме при проектировании (5.5) на оси связанной СК, ориентированных вдоль главных осей инерции самолета (ракеты), для которых центробежные моменты инерции нулевые (I_xz=I_yz=0), а значения I_xy - малы. Из курса теоретической механики известно, что уравнения вращательного движения ЛА в проекциях (5.5) на OXYZ запишутся в виде [1], [2]

; (5.12)

; (5.13)

, (5.14)

где: – проекции вектора угловой скорости вращения ЛА на главные центральные оси инерции;

M_x, M_y, M_z – сумма проекций моментов сил, входящих в правую часть (5.5), соответственно на оси OX, OY, OZ;

I_x, I_y, I_z – главные центральные моменты инерции ЛА, являющиеся функциями массы: I_x(m), I_y(m), I_z(m).

Уравнения движения центра масс (5.6) вертолета часто используют в проекциях на связанные оси координат OXYZ в следующей форме ([2], стр.40):

; (5.15)

; (5.16)

. (5.17)

Здесь V_x, V_y, V_z, – проекции векторов линейной и угловой скорости и соответственно на оси OX, OY, OZ; X, Y, Z – проекции сил, входящих в правую часть (5.6), соответственно на оси OX, OY и OZ.

Уравнения вращательного движения вертолета в проекциях на оси связанной СК имеют вид (5.12) – (5.14), в которых M_x, M_y, M_z определяются как сумма проекций моментов, входящих в правую часть (5.7), соответственно на оси OX, OY и OZ.

Отметим, что если для вертолета или любого другого ЛА значение центробежного момента инерции I_xy является существенной величиной, то можно использовать уравнения в форме (1.57) [1] стр.33.

Обычно в математической модели движения вертолета к системам уравнений (5.12) – (5.14) добавляют уравнение равновесия моментов относительно вала несущего винта

, (5.18)

где M_yв – суммарный крутящий момент, обусловленный несущими винтами вертолёта, и момента, создаваемого силовой установкой; I_yв- приведённый момент инерции вращающихся элементов относительно вала несущего винта; - угловая скорость вращения винта.