- •Часть I.
- •11.2.3. Решение линейных дифференциальных уравнений
- •11.2.5. Исследование управляемого движения с помощью
- •Лекция 1.
- •Введение. Предмет курса
- •Характеристики Земли, ее атмосферы (см. Рис.1)
- •Лекция 2.
- •Аэродинамические силы и продольный момент изолированного крыла
- •Пример 1 (см. Рис. 10).
- •Пример 2.
- •Пример 3 (рис.11).
- •Лекция 3.
- •Полная аэродинамическая сила и продольный момент ла
- •4 Рис. 16 .1 Аэродинамические характеристики крыла
- •4.2 Системы координат и углы, определяющие положение ла в пространстве
- •Лекция 4.
- •4.3 Полная аэродинамическая сила всего ла
- •Примеры
- •4.4.Полный момент ла, обусловленный аэродинамическими силами
- •Уравнения движения ла
- •5.1 Уравнения движения в векторной форме
- •Лекция 5.
- •5.2 Уравнения движения ла в скалярной форме
- •Кинематические уравнения. Связь между углами
- •6. 1 Кинематические уравнения движения центра масс (цм) ла можно получить, разложив векторное уравнение
- •6.2 Кинематические уравнения, описывающие вращение ла относительно нормальной системы координат (рис.24) Вид по стрелке а
- •Лекция 6.
- •Уравнения движения центра масс ла в частных случаях
- •7.1 Полёт без крена и скольжения относительно сферической невращающейся Земли при отсутствии ветра
- •7.2 Полет без крена и скольжения относительно плоской невращающейся Земли при отсутствии ветра.
- •7.3 Горизонтальный полет с креном и без скольжения
- •7.4 Перегрузка. Уравнения движения центра масс в безразмерной форме
- •Лекция 8.
- •8.2 Установившийся набор высоты. Скороподъемность ла
- •8.3 Особенности летных характеристик и динамики вертолета
- •Лекция 9.
- •8.4. Диапазон высот и скоростей полета вертолета
- •8.5 Установившееся снижение самолета. Планирование
- •8.6 Виражи.
- •8.7 Правильный вираж (без скольжения, с креном и постоянной скоростью).
- •Лекция 10.
- •Методы наведения при атаке воздушной цели
- •9.1 Область возможных атак по методу погони
- •Лекция 11.
- •9.2 Движение ракеты в плотных слоях атмосферы
- •Лекция 12.
- •10. Устойчивость и управляемость движения
- •10.1. Виды устойчивости движения
- •10.2. Статическая и динамическая устойчивость и управляемость ла
- •Лекция 13.
- •10.3. Управление движением ла. Использование автоматических средств управления
- •Лекция 14.
- •10.4. Показатели статической устойчивости и управляемости
- •Лекция 15.
- •10.5 Диапазон центровок ла
- •11.Исследование возмущённого движения ла
- •11.1 Уравнения возмущённого движения ла
- •Лекция 16.
- •11.2 Математические методы исследования
- •11.2.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методом
- •11.2.2 Алгебраические критерии устойчивости
- •Лекция 17.
- •11.2.3 Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом
- •Пример.
- •11.2.4 Исследование управляемого движения с помощью передаточных функций
- •11.2.5 Исследование управляемого движения с помощью частотных характеристик
- •Литература Основная
- •Дополнительная
8.5 Установившееся снижение самолета. Планирование
(Уравнения те же, что и при подъеме, только <0)
1) P=mg sin;
2) Ya=mg cos=CyaqS,
P(+) мало в 2)
После деления 1) на 2)
![]() ,
с учетом того, что P<0
и <0.
,
с учетом того, что P<0
и <0.
Отсюда:
![]() ;
(если тяга выключена или мала при
планировании),
;
(если тяга выключена или мала при
планировании),
![]() ,
т.к.
,
т.к.
![]() из 2), то
из 2), то
 ;
; ![]() ;
;
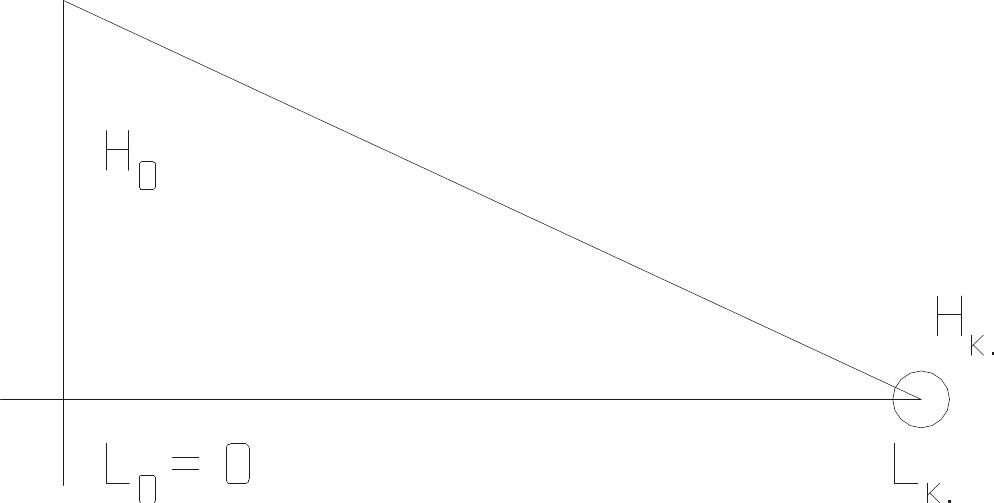
Рис.45
Поскольку:

то после деления:
![]() ;
и интегрируя левую и правую часть,
получаем (см. рис. 45):
;
и интегрируя левую и правую часть,
получаем (см. рис. 45):
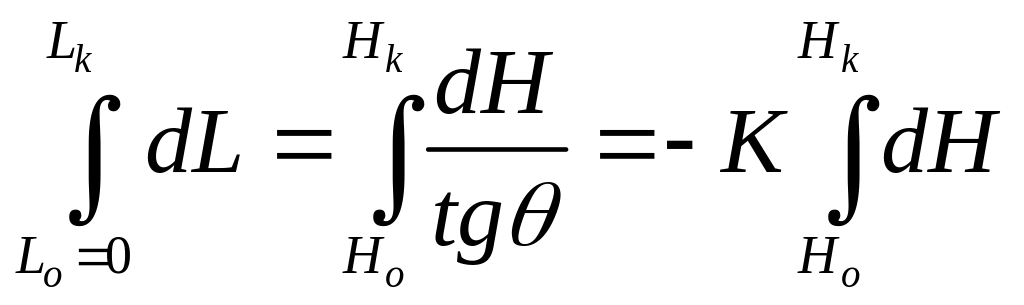 , =const
; Lk=-K(Hk-H0)=K(H0-Hk),
, =const
; Lk=-K(Hk-H0)=K(H0-Hk),
Lkmax=Kmax(H0-Hk), если Hk=0, то Lkmax=Kmax H0.
8.6 Виражи.
Вираж - разворот в горизонтальной плоскости на 360○. При V=const, γa=const, β=0 – вираж правильный.
Разворот с минимальным радиусом и с торможением называется форсированным виражем.
Схема сил при полете с креном и скольжением см. на рис. 46.
1
Рис.
46
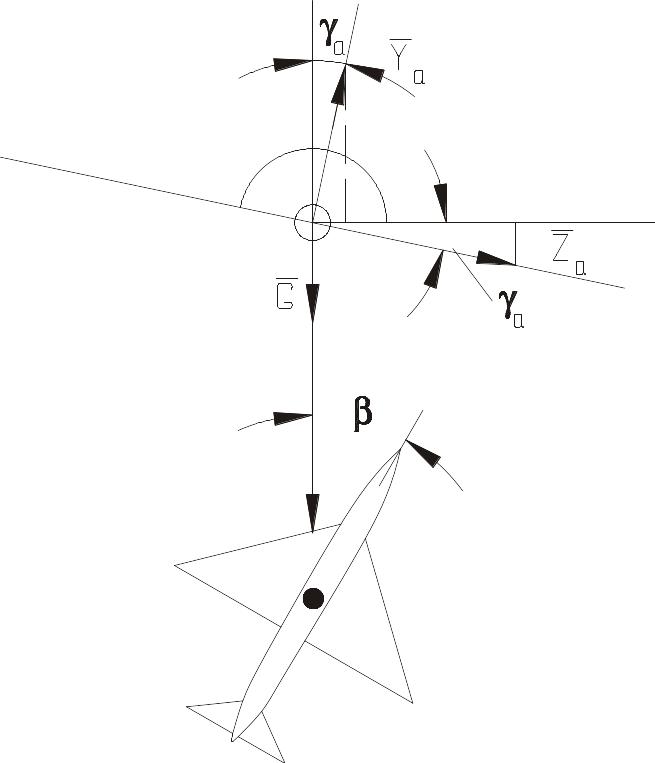
![]() ;
;
2) (проекция на вертикаль) Yacosγa-Zasinγa=G;
Если посмотреть
на уравнения движения относительно
плоской невращающейся Земли
(см.(7.19)-(7.21)), то
nxa=sinθ=0; nyacosγa-nzasinγa=cosθ=1; nyasinγa+nzacosγa=![]() ,
,
что соответствует 1) и 2), если поделить правую и левую часть на G.
В результате получаем
1)![]() ;
;
2)![]() (угловая
скорость поворота).
(угловая
скорость поворота).
Если разворот
только с креном
![]() и β=0 без скольжения (координированный
вираж), то Za=0
и nza=0.
и β=0 без скольжения (координированный
вираж), то Za=0
и nza=0.
1)![]() ;
(8.22)
;
(8.22)
2)![]() ,
(8.23) (т.к.
,
(8.23) (т.к.
![]() ;
;
![]() )
)
8.7 Правильный вираж (без скольжения, с креном и постоянной скоростью).
![]() ;
Rв=const,
nXa=0;
(8.24)
;
Rв=const,
nXa=0;
(8.24)
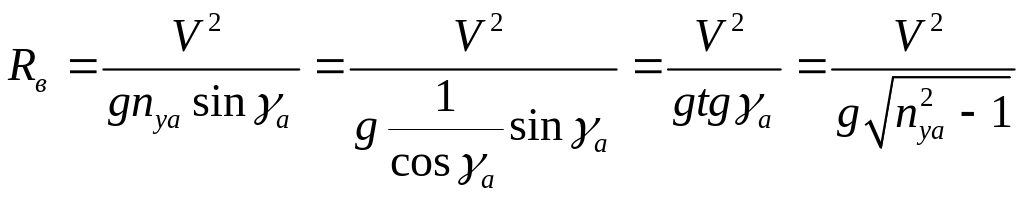 .
(8.25)
.
(8.25)
Время выполнения виража
![]() ,
(8.26)
,
(8.26)
т.е. достаточно знать V и nуа или V и γa, чтобы рассчитать характеристики виража.
Предельные характеристики виража, т.е. минимальные и максимальные характеристики вычисляются с учетом допустимых перегрузок, например,
![]() , (при V=const)
(8.27)
, (при V=const)
(8.27)
![]() и т.д. (8.28)
и т.д. (8.28)
Аналогично рассчитываются различные маневры самолетов и вертолетов.
Лекция 10.
Методы наведения при атаке воздушной цели
9.1 Область возможных атак по методу погони
При ведении воздушного боя можно выделить следующие этапы: поиск, сближение, атака, выход из атаки. При исследовании воздушного боя применяют критерии: вероятность сбития противника, разность вероятностей сбития самолета противника и своего самолета, отношение вероятностей сбития самолета противника и своего самолета. Исследования обычно проводятся с помощью теории игр, а затем моделируются на стендах.
Сближение осуществляется различными методами наведения: погоня, параллельное сближение, пропорциональное сближение и др.
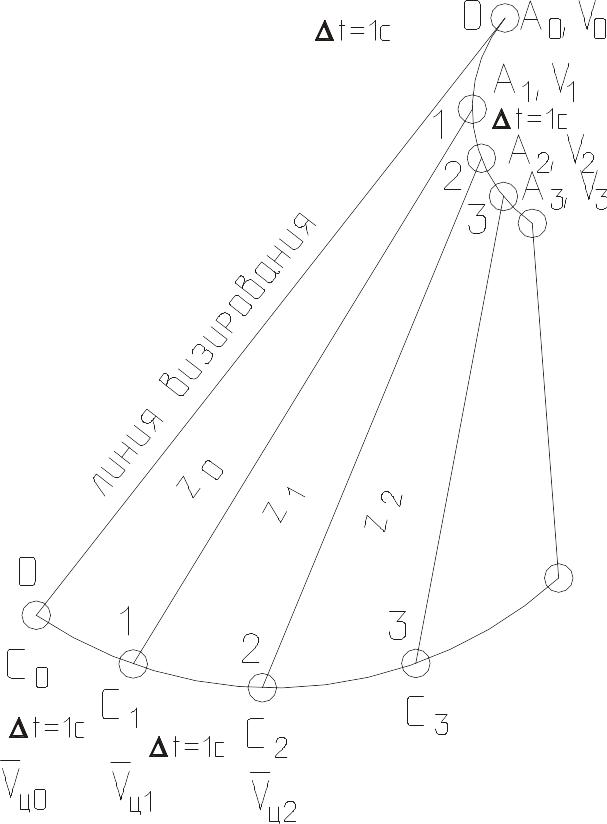
При погоне
вектор скорости атакующего самолета
всегда направлен на цель. Если принять
![]() ,
то путь, пройденный каждым самолетом
равен скорости. Пусть в первую секунду
самолёт движется примерно по направлению
А0С1 (на больших дальностях)
проходя путь А0А1, численно
равный V0. (рис. 47).
,
то путь, пройденный каждым самолетом
равен скорости. Пусть в первую секунду
самолёт движется примерно по направлению
А0С1 (на больших дальностях)
проходя путь А0А1, численно
равный V0. (рис. 47).
Рис. 47а) |
Рис. 47б) |
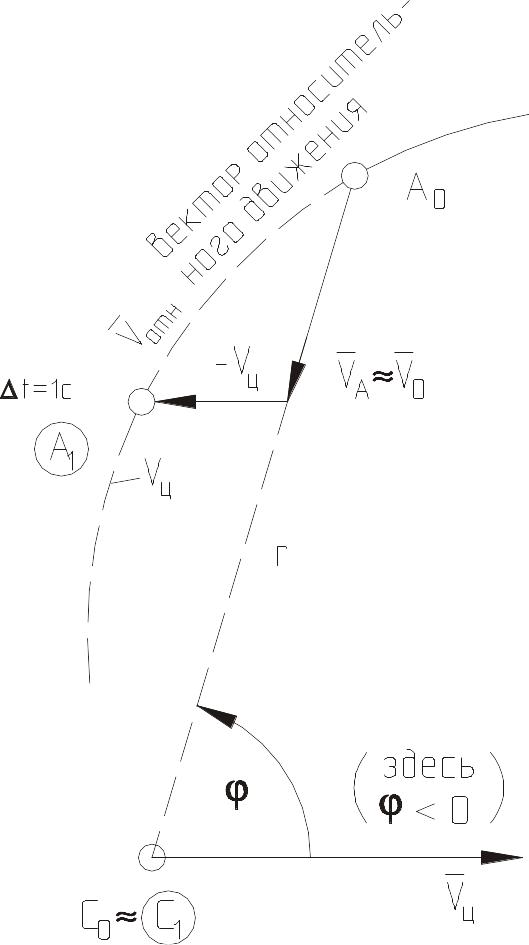
Цель «как бы останавливается», и относительное движение рассматривается по принципу «обращения движения».
Относительное движение атакующего самолёта описывается следующими кинематическими уравнениями:

где: - курсовой угол; r – расстояние между самолётами – относительная дальность.
Определим потребную нормальную скоростную перегрузку при движении по кривой погони.
Потребная угловая скорость (пусть движение происходит в горизонтальной плоскости)
угловые скорости

![]() (9.1)
(9.1)
потребная располагаемая
равна располагаемой.
Отсюда
![]()
![]() (9.2)
(9.2)
и потребная перегрузка атакующего
![]() (9.3)
(9.3)
П
Рис.
48
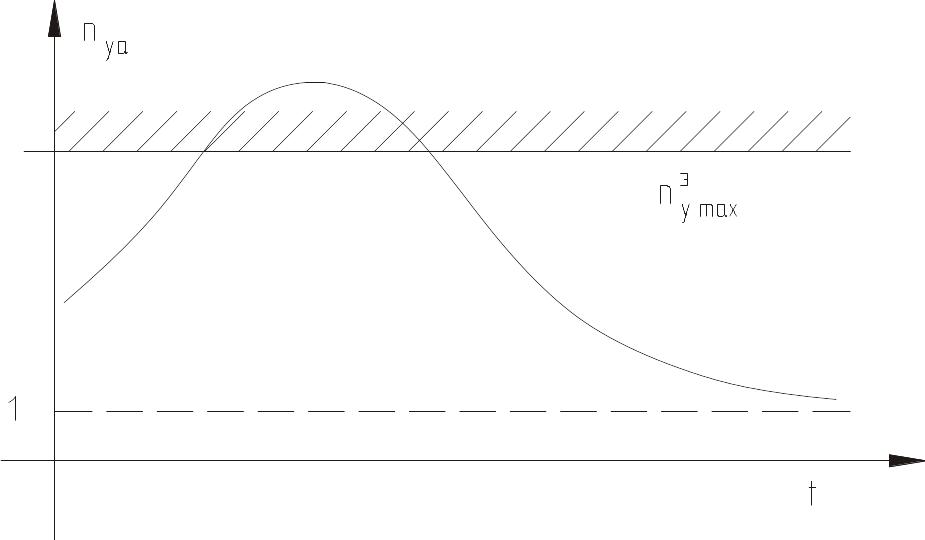
![]() дан на рисунке 48. Видно, что возможны
случаи, когда атака не может
быть выполнена, то есть погоня невозможна.
Поэтому важно знать область, из
которой погоня невозможна.
дан на рисунке 48. Видно, что возможны
случаи, когда атака не может
быть выполнена, то есть погоня невозможна.
Поэтому важно знать область, из
которой погоня невозможна.
Из (9.2) при
заданных
![]() ,
Vц=const,
V=const
,
Vц=const,
V=const
 ;
;
с учётом (8.25)


![]()
Минимальному
rmin
соответсвует
![]()
Это
уравнение двух окружностей, которые
касаются вектора
![]() в центре масс цели. Из внутренних
областей, выделенных окружностями
погоня невозможна.
в центре масс цели. Из внутренних
областей, выделенных окружностями
погоня невозможна.
Dmin обусловлена безопасностью,
Dmax - определяется максимальной дальностью стрельбы.
Это - характерные области, обусловленные методом погони. Область, из которой возможна погоня, ограничена линиями Dmin , Dmax и окружностями зависящими от предельных эксплуатационных перегрузок.