- •Часть I.
- •11.2.3. Решение линейных дифференциальных уравнений
- •11.2.5. Исследование управляемого движения с помощью
- •Лекция 1.
- •Введение. Предмет курса
- •Характеристики Земли, ее атмосферы (см. Рис.1)
- •Лекция 2.
- •Аэродинамические силы и продольный момент изолированного крыла
- •Пример 1 (см. Рис. 10).
- •Пример 2.
- •Пример 3 (рис.11).
- •Лекция 3.
- •Полная аэродинамическая сила и продольный момент ла
- •4 Рис. 16 .1 Аэродинамические характеристики крыла
- •4.2 Системы координат и углы, определяющие положение ла в пространстве
- •Лекция 4.
- •4.3 Полная аэродинамическая сила всего ла
- •Примеры
- •4.4.Полный момент ла, обусловленный аэродинамическими силами
- •Уравнения движения ла
- •5.1 Уравнения движения в векторной форме
- •Лекция 5.
- •5.2 Уравнения движения ла в скалярной форме
- •Кинематические уравнения. Связь между углами
- •6. 1 Кинематические уравнения движения центра масс (цм) ла можно получить, разложив векторное уравнение
- •6.2 Кинематические уравнения, описывающие вращение ла относительно нормальной системы координат (рис.24) Вид по стрелке а
- •Лекция 6.
- •Уравнения движения центра масс ла в частных случаях
- •7.1 Полёт без крена и скольжения относительно сферической невращающейся Земли при отсутствии ветра
- •7.2 Полет без крена и скольжения относительно плоской невращающейся Земли при отсутствии ветра.
- •7.3 Горизонтальный полет с креном и без скольжения
- •7.4 Перегрузка. Уравнения движения центра масс в безразмерной форме
- •Лекция 8.
- •8.2 Установившийся набор высоты. Скороподъемность ла
- •8.3 Особенности летных характеристик и динамики вертолета
- •Лекция 9.
- •8.4. Диапазон высот и скоростей полета вертолета
- •8.5 Установившееся снижение самолета. Планирование
- •8.6 Виражи.
- •8.7 Правильный вираж (без скольжения, с креном и постоянной скоростью).
- •Лекция 10.
- •Методы наведения при атаке воздушной цели
- •9.1 Область возможных атак по методу погони
- •Лекция 11.
- •9.2 Движение ракеты в плотных слоях атмосферы
- •Лекция 12.
- •10. Устойчивость и управляемость движения
- •10.1. Виды устойчивости движения
- •10.2. Статическая и динамическая устойчивость и управляемость ла
- •Лекция 13.
- •10.3. Управление движением ла. Использование автоматических средств управления
- •Лекция 14.
- •10.4. Показатели статической устойчивости и управляемости
- •Лекция 15.
- •10.5 Диапазон центровок ла
- •11.Исследование возмущённого движения ла
- •11.1 Уравнения возмущённого движения ла
- •Лекция 16.
- •11.2 Математические методы исследования
- •11.2.1 Решение линейных дифференциальных уравнений с постоянными коэффициентами классическим методом
- •11.2.2 Алгебраические критерии устойчивости
- •Лекция 17.
- •11.2.3 Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом
- •Пример.
- •11.2.4 Исследование управляемого движения с помощью передаточных функций
- •11.2.5 Исследование управляемого движения с помощью частотных характеристик
- •Литература Основная
- •Дополнительная
Лекция 8.
8.2 Установившийся набор высоты. Скороподъемность ла
Воспользуемся методом тяг. q¹0, V = const,
по (7.6) ![]() .
.
Отсюда
![]() ,
(8.13)
,
(8.13)
т.к. с изменением высоты
Рнб. изменяется, то
sinq
также должен быть переменным. Однако
темп изменения q
обычно невелик и в уравнении (7.2), полагая
(Rз + H)®¥,
![]() ,
получаем
,
получаем
или
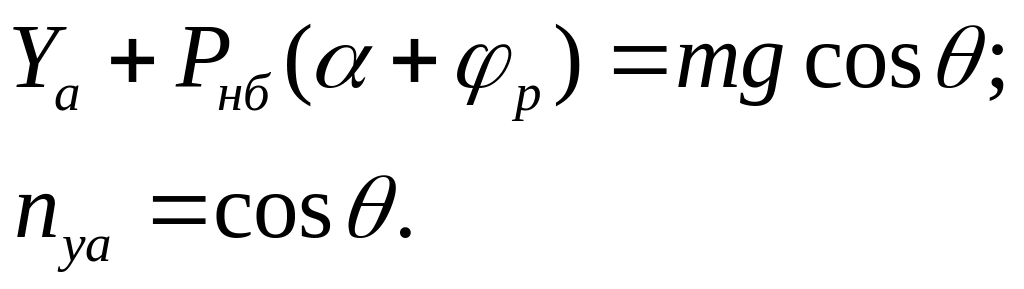 (8.14)
(8.14)
Отсюда можно выразить потребное значение коэффициента подъемной силы Суа.нб и следовательно aнб при наборе на данном q, учитывая (8.4)
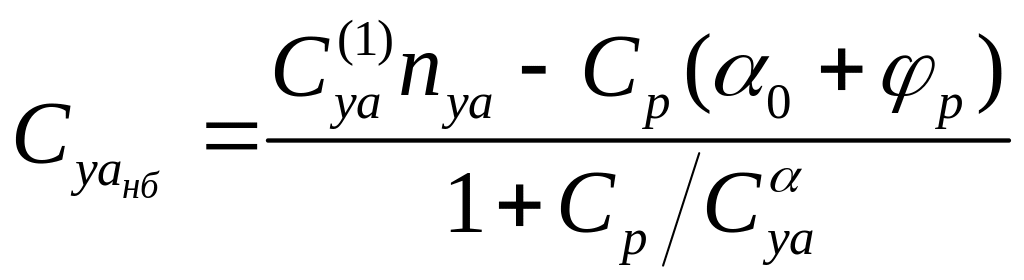 ,
(8.15)
,
(8.15)
где
![]() ;
nya
определяется по (8.14) для q
из (8.13), а коэффициент тяги Сp
соответствует заданному режиму работы
двигателя
;
nya
определяется по (8.14) для q
из (8.13), а коэффициент тяги Сp
соответствует заданному режиму работы
двигателя
![]() .
(8.16)
.
(8.16)
Решая совместно (8.15), (8.16) при известных Cxa (Cya) и Рнб (V,H) можно при заданных V, H найти угол q, а значит и Vy, т. к.
Vy=Vsinq (8.17)
и значение Cуа нб. Решение, как и ранее, удобно, проводить методом последовательных приближений. Последовательность расчетов следующая.
В первом приближении при заданных V и H для по поляре определяется
![]() ,
,
далее определяется sinq по (8.13). В этом случае
![]() ,
,
что позволяет использовать
кривые потребных тяг, построенные
ранее.
![]() – определяется графически. Найдя sinq1
в первом приближении, можно по (8.15)
определить Суа нб. Затем по
поляре рассчитать Сха(Cya
нб) и повторить весь расчет
снова по уточненному Сха.
– определяется графически. Найдя sinq1
в первом приближении, можно по (8.15)
определить Суа нб. Затем по
поляре рассчитать Сха(Cya
нб) и повторить весь расчет
снова по уточненному Сха.
Учитывая, что
![]() ,
можно построить (
,
можно построить (![]() - обозначен относительный избыток
располагаемой мощности) зависимости
Vy(V)
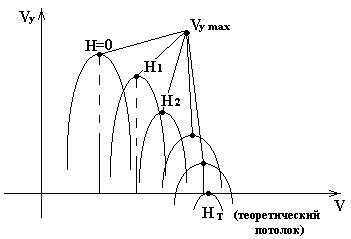
(рис. 33) и зависимости H
(Vymax)
(рис. 34).
- обозначен относительный избыток
располагаемой мощности) зависимости
Vy(V)
(рис. 33) и зависимости H
(Vymax)
(рис. 34).
Рис. 33 |
Рис.34 |
Решая уравнение
(6.2)
![]() ,
,
![]() с учетом (8.17) вычислим
с учетом (8.17) вычислим
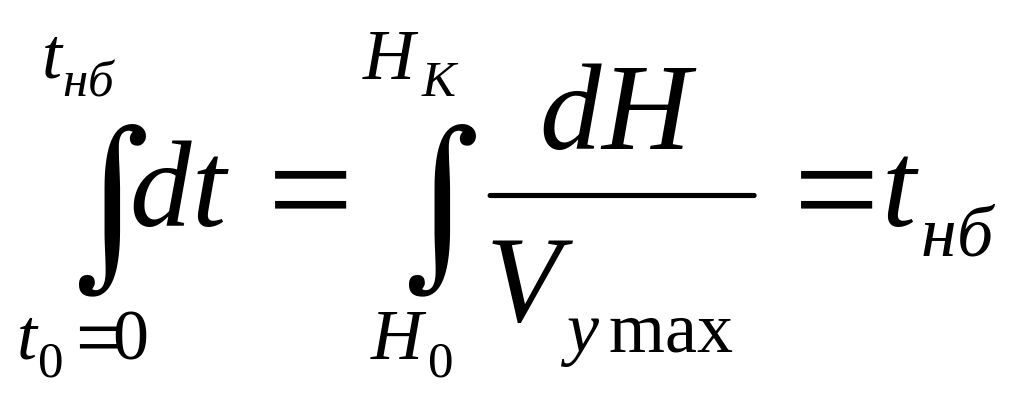 (часто
решают графо-аналитически)
(часто
решают графо-аналитически)
Здесь Vy=Vy max, т.к. принимаются max значения, чтобы получить tmin= tнб.
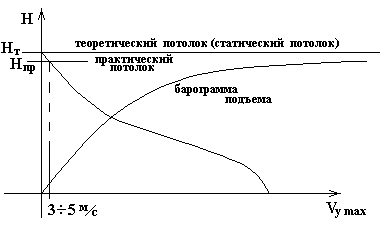
Зная Vу max(V) для различных Нi, можно нанести зависимость Н(V), где будет скорейший подъем (tmin) (рис. 35).
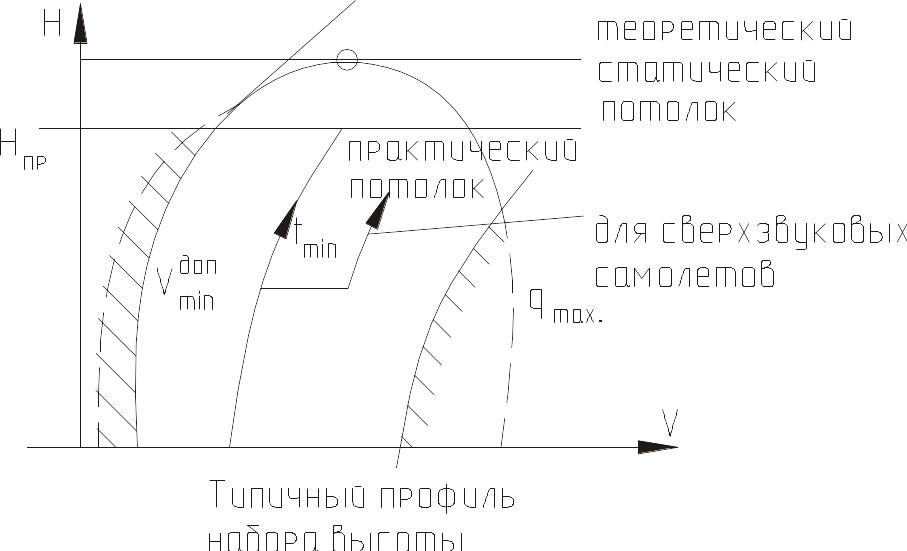
Рис. 35
8.3 Особенности летных характеристик и динамики вертолета
Рассмотрим
схему сил, действующих на вертолет в
вертикальной плоскости. (Проекции
представлены на траекторные оси
координат,
![]() ,
полет без крена и скольжения, рис.36)
,
полет без крена и скольжения, рис.36)
Рис.
36
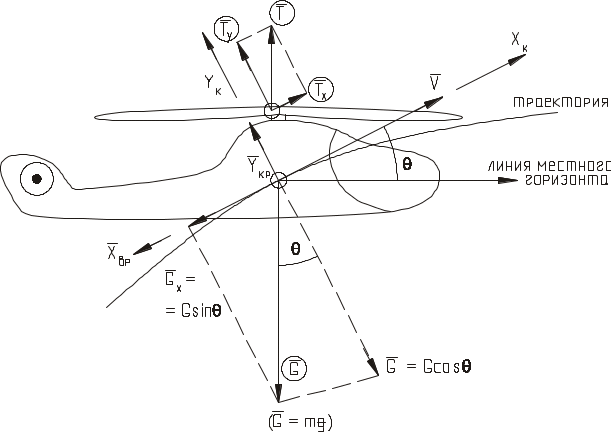
![]() -
полная аэродинамическая сила;
-
полная аэродинамическая сила;
![]() - пропульсивная сила;
- пропульсивная сила;
![]() - подъемная сила несущего винта;
- подъемная сила несущего винта;
![]() - подъемная сила фюзеляжа ( планера);
- подъемная сила фюзеляжа ( планера);
![]() -
вредное лобовое сопротивление фюзеляжа
(планера).
-
вредное лобовое сопротивление фюзеляжа
(планера).
Согласно (5.6), (5.8) и (5.9)
 (8.18)
(8.18)
Для расчета и анализа летных
характеристик вертолета применяют
метод мощностей. Располагаемая мощность
вертолета
![]() .
Потребная мощность равна
.
Потребная мощность равна
![]() .
(8.19)
.
(8.19)
Здесь
Рис.
37![]() – мощность, затрачиваемая на преодоление
вредного сопро- тивления;
– мощность, затрачиваемая на преодоление
вредного сопро- тивления;
![]() - мощность, затра-чиваемая на преодоление
профильного сопротивления лопастей
несущего винта;
- мощность, затра-чиваемая на преодоление
профильного сопротивления лопастей
несущего винта; 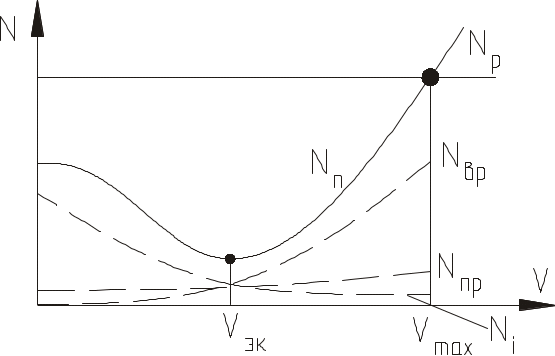 Рис.37
Рис.37
![]() - мощность, затрачиваемая на преодоление
индуктивного сопротивления лопастей
несущего винта.
- мощность, затрачиваемая на преодоление
индуктивного сопротивления лопастей
несущего винта.
З![]()
 ависимости
ависимости
![]() ,
,![]() для вертолета в прямолинейном
горизонтальном полете приведены на
рис. 37.
для вертолета в прямолинейном
горизонтальном полете приведены на
рис. 37.
На малых
скоростях
![]() велика;´ из-за большого индуктивного
сопротивления лопастей. Однако даже
при V=0, в отличие
от самолета, может быть меньше
располагаемой. Это обеспечивает висение
вертолета. При больших скоростях
потребная мощность увеличивается из-за
роста сопротивления
и профильного сопротивления лопастей.
При экономической скорости
велика;´ из-за большого индуктивного
сопротивления лопастей. Однако даже
при V=0, в отличие
от самолета, может быть меньше
располагаемой. Это обеспечивает висение
вертолета. При больших скоростях
потребная мощность увеличивается из-за
роста сопротивления
и профильного сопротивления лопастей.
При экономической скорости
![]() потребная мощность минимальна.
потребная мощность минимальна.