§4. Графический метод решения матричной игры

Иногда после исключения доминируемых стратегий получается игра, в которой один из игроков имеет в своем распоряжении только две чистых стратегии, т.е. размерность платежной матрицы равна или . Если эта игра неразрешима в чистых стратегиях (не имеет седловой точки), то ее решение достаточно просто найти с помощью графического метода.

В его основе лежит графическое представление игры. После определения активных стратегий игроков ее решение сводится к описанному выше случаю (см. стр. 150).

1. Игра

Предположим сначала, что первый игрок имеет две чистых стратегии, а второй игрок — n чистых стратегий, т.е. , а .

Тогда платежная матрица игры выглядит так:

.

Множество смешанных стратегий игроков имеет такой вид:

• для игрока 1 — ;

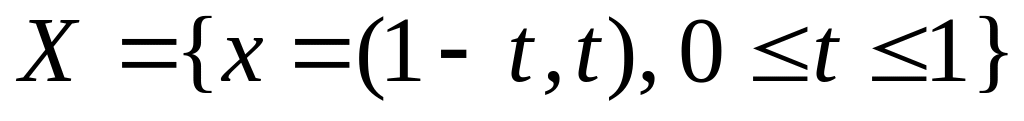• для игрока 2 — .

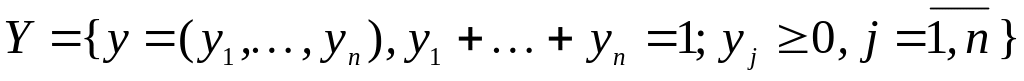Обозначим — выигрыш игрока 1 в ситуации, когда он выбрал смешанную стратегию , а игрок 2 — свою чистую стратегию . Тогда ясно, что

.

Обозначим — гарантированный выигрыш игрока 1 при выборе им стратегии . Тогда по теореме 3.1 для игрока 1 оптимальной будет стратегия , которой соответствует значение , дающее максимум функции на отрезке [0, 1], т.е.

.

Все функции являются линейными функциями от переменной t. Поэтому функция будет вогнутой кусочно-линейной функцией на [0, 1]. Она является нижней огибающей семейства функций { } на этом отрезке, а ее график «склеен» из отдельных участков прямых .

Максимум равен цене игры . Он может быть легко найден, если сначала построить графически семейство прямых , а затем график самой функции .

По теореме 3.5 все стратегии игрока 2, для которых > , могут быть отброшены. Как правило, активными будут лишь две стратегии этого игрока. Это позволяет свести решение игры к уже изученному ранее случаю игры .

Пример 4.1. Нужно найти решение игры, задаваемой матрицей

.

Сначала проверим, есть ли у этой игры решение в чистых стратегиях. Для этого найдем и = 4. Так как они не равны друг другу, то решения в чистых стратегиях нет.

Для нахождения решения в смешанных стратегиях применим графический метод. На плоскости tOZ введем систему координат и на оси Ot отложим единичный отрезок [0, 1], каждой точке t которого сопоставим смешанную стратегию игрока 1.

В точках 0 и 1 проведем линии, перпендикулярные оси Ot. На первом перпендикуляре, совпадающем с осью OZ, отложим значения элементов первой строки матрицы А — выигрыши игрока 1 при выборе им чистой стратегии . На втором перпендикуляре отложим значения элементов второй строки — его выигрыши при выборе чистой стратегии . Тогда для получения графика функции достаточно соединить точки на перпендикулярах, соответствующие чистой стратегии игрока 2.

Например, чтобы получить график функции , следует соединить точку 1 на левом перпендикуляре с точкой 7 на правом перпендикуляре, поскольку числа 1 и 7 — элементы первого столбца матрицы А.

Эта функция имеет такой вид:

.

Соответственно,

,

,

.

Тогда функция задает минимальный выигрыш игрока 1 при выборе им смешанной стратегии .

Она является нижней огибающей семейства прямых , а ее график состоит из трех отрезков прямых. На рис. 4.1 он выделен жирной линией АВСD. Аналитически эта функция записывается в таком виде:

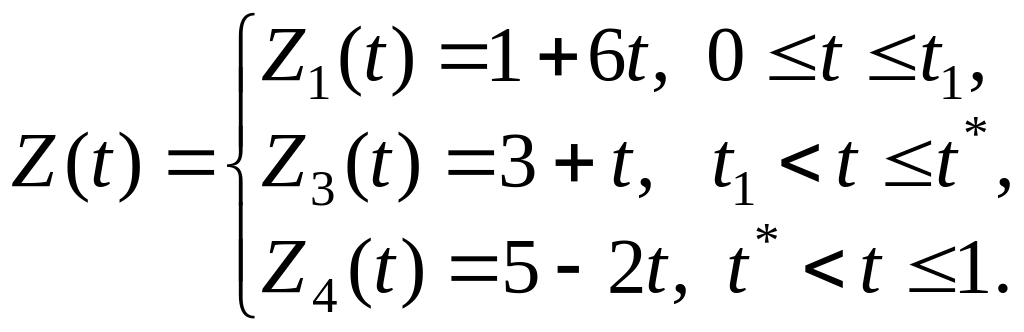
Функция не участвует в формировании . Это связано с тем, что стратегия игрока 2 доминирует над его стратегией .

М

Рис. 4.1. Графический метод решения игры

аксимального значения функция достигает в точке . Эта точка, как уже говорилось выше, соответствует оптимальной смешанной стратегии игрока 1, а длина отрезка ЕС равна цене игры .

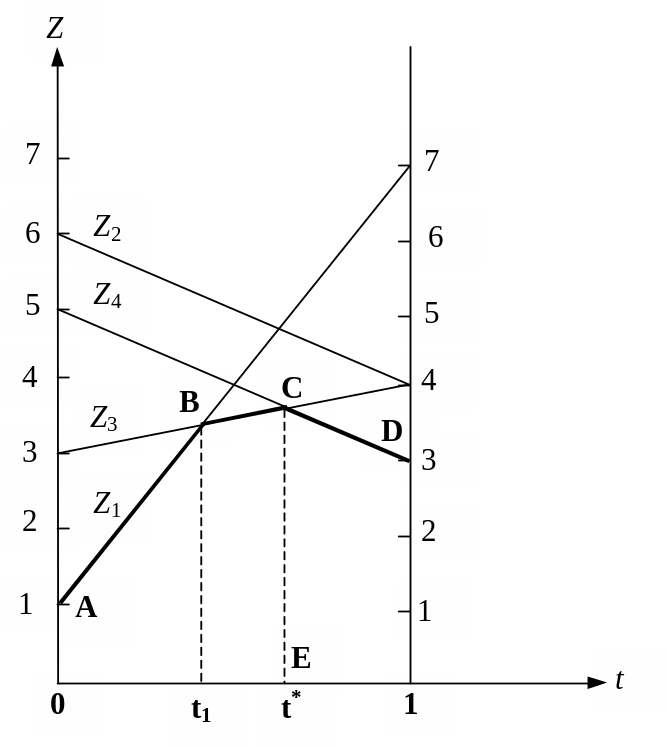
Для нахождения решения игры нужно использовать следующие соображения. В точке С = ( , ) пересекаются две прямые и , т.е. . Это говорит о том, что стратегии и игрока 2 являются активными. Так как и , то по теореме 3.5 стратегии и игрока 2 не могут быть активными, т.е. . Следовательно, соответствующие столбцы матрицы А можно вычеркнуть.

Таким образом, исходная игра сведена к игре, задаваемой матрицей размерности :

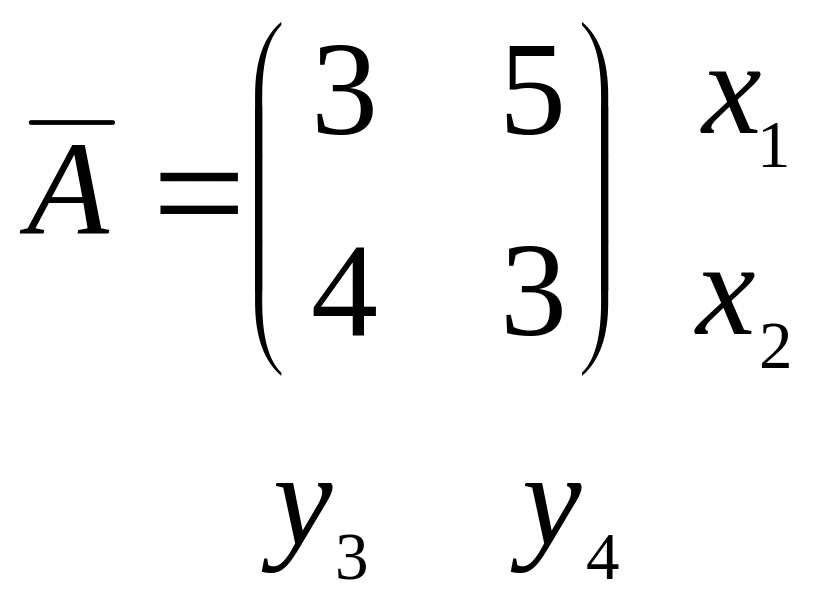
Для определения цены этой игры и оптимальной смешанной стратегии игрока 1 следует решить систему уравнений:

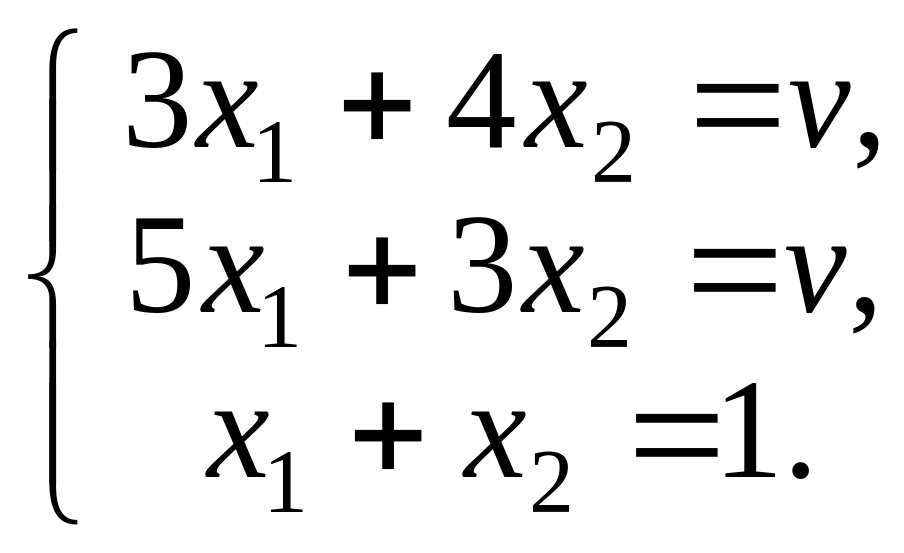
Вычтя из первого уравнения второе, получим, что . Значит, , а .

Для нахождения коэффициентов активных стратегий игрока 2 нужно решить систему уравнений:

Ее решение: . Итак, исходная игра имеет решение:

.