
- •Содержание
- •1. Организация таблицы идентификаторов
- •1.1 Исходные данные
- •1.2 Назначение таблиц идентификаторов
- •1.3 Хеш-адресация с рехешированием.
- •1.4 Упорядоченный список
- •1.5 Результаты
- •2. Проектирование лексического анализатора
- •2.1 Исходные данные
- •2.2 Принципы работы лексического анализатора
- •2.3 Схема распознавателя
- •2.4 Результаты
- •3.1 Исходные данные
- •3.2 Построение синтаксического анализатора
- •Список литературы
1.2 Назначение таблиц идентификаторов
Таблица идентификаторов (ТИ) – это специальным образом организованный набор данных, который служит для хранения информации об исходной программе. Каждое поле таблицы содержит всю необходимую компилятору информацию об элементе, может пополняться по мере работы компилятора. Под идентификаторами подразумеваются константы, переменные, имена процедур и функций, формальные и фактические параметры.
Структура данных таблицы идентификаторов должна содержать в обязательном порядке поле имени идентификатора, а также поля дополнительной информации об идентификаторе по усмотрению разработчиков компилятора, но в курсовом проекте хранение какой-либо дополнительной информации об идентификаторах можно не организовывать. Таблицы идентификаторов реализованы в виде статических массивов.
1.3 Хеш-адресация с рехешированием.
Хэш-адресация
заключается в использовании значения,
возвращаемого хэш-функцией, в качестве
адреса ячейки из некоторого массива
данных. В курсовом проекте хэш-функция
будет выдавать сумму кодов первого
и второго элементов строки, если  строка
содержит один символ, то хэш-функция
берется от одного элемента.
строка
содержит один символ, то хэш-функция
берется от одного элемента.
Для решения проблемы коллизии используем метод рехеширования с помощью произведения, новую хеш-функцию получаем по формуле:
hi(A) = ( h(A)∙i ) mod Nm, (1)
где i – число возникновения коллизий, а Nm – максимальное значение из области значений (равное 509).
Согласно этому методу – хеш-адресации – если для элемента A адрес n0 = h(А), вычисленный с помощью хэш-функции, указывает на уже занятую ячейку, то необходимо вычислить значение функции n1 = h1(А) и проверить занятость ячейки по адресу n1. Если и она занята, то вычисляется значение h2(A), и так до тех пор, пока либо не будет найдена свободная ячейка, либо очередное значение hi(A) не совпадет с h(А). В последнем случае считается, что таблица идентификаторов заполнена и места в ней больше нет — выдается информация об ошибке размещения идентификатора в таблице.
В целом рехеширование позволяет добиться неплохих результатов для эффективного поиска элемента в таблице, но эффективность метода сильно зависит от заполненности таблицы идентификаторов и качества используемой хеш-функции – чем реже возникают коллизии, тем выше эффективность. Требование неполного заполнения таблицы ведет к неэффективному использованию объема доступной памяти.
Блок-схема добавления и поиска элемента в таблице идентификаторов методом хеш-адресации представлен на рис. 1 и рис. 2.
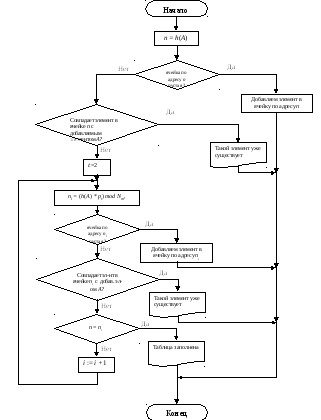
 Рис.
1 Блок-схема добавления элемента методом
хеш-адресации
Рис.
1 Блок-схема добавления элемента методом
хеш-адресации
Блок-схема поиска элемента в таблице идентификаторов методом хеш-адресации представлена на рис. 2.

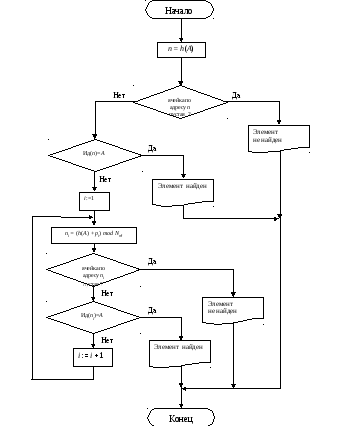
Рис.2 Блок-схема поиска элемента в ТИ методом хеш-адресации
1.4 Упорядоченный список
Метод организации таблицы идентификаторов, в котором при добавлении надо перестраивать весь список, т.е. упорядочивать его согласно некоторому условию.
В этом методе применяется бинарный или логарифмический способ поиска элементов. Алгоритм этого поиска заключается в следующем: искомый символ сравнивается с элементом (N+1)/2 в середине таблицы; если этот элемент не является искомым, то мы должны просмотреть только блок элементов, пронумерованных от 1 до (N+1)/2 – 1, или блок элементов от (N+1)/2 + 1 до N в зависимости от того, меньше или больше искомый элемент того, с которым его сравнивали. Затем процесс повторяется с блоком в два раз меньшего размера. Так продолжается до тех пор, пока либо не будет найден искомый элемент, либо алгоритм не дойдет до очередного блока.
 Так
как на каждом шаге число элементов,
которые могут содержать искомый элемент,
сокращается в 2 раза, максимальное число
сравнений равно 1+log2(N).
Так
как на каждом шаге число элементов,
которые могут содержать искомый элемент,
сокращается в 2 раза, максимальное число
сравнений равно 1+log2(N).
Недостатком данного метода в том, что для поиска требуется упорядочивание таблицы идентификаторов, следовательно, время заполнения будет зависеть от числа добавляемых элементов.
Блок-схемы добавления и поиска элемента в упорядоченном списке представлены на рис. 3 и рис. 4.

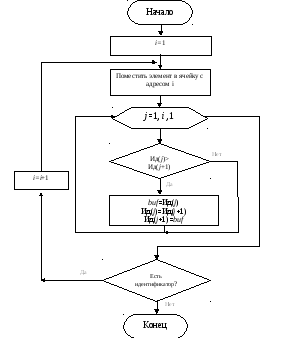
Рис. 3. Блок-схема алгоритма добавления элемента в упорядоченный список
min(начало
блока элементов)=1;
max(конец
блока элементов)=N;
max=(
max-min)/2-1
Нет
Да
Да
Нет
min=(
max-min)/2+1




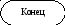




















Рис. 4 Блок-схема алгоритма поиска элемента в упорядоченном списке
