
- •Оглавление Линейная алгебра с элементами аналитической геометрии
- •I. Практические занятия
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 3 “Элементы векторной алгебры” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Практическое занятие № 4 “Аналитическая геометрия” Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •II. Тесты
- •Вариант № 2
- •Вариант № 3
- •Вариант № 4
- •Вариант № 5
- •Тест № 2
- •Вариант № 1
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 2
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 3
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 4
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 5
- •1) Знаконеопределенной; 2) отрицательно определенной;
- •3) Положительно определенной;
- •Вариант № 1
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 2
- •1) Эллипс; 2) параболу; 3) окружность;
- •Вариант № 3
- •1) Эллипс; 2) параболу; 3) гиперболу;
- •Вариант № 4
- •1) Эллипс; 2) окружность; 3) гиперболу;
- •Вариант № 5
- •1) Эллипс; 2) окружность; 3) параболу;
- •III. Решение типовых примеров Типовые примеры к практическому занятию № 1
- •Типовые примеры к практическому занятию № 2
- •Решение. Умножим слева обе части уравнения на , а справа – на . Тогда . В результате получаем решение системы . Теперь следует определить обратные матрицы:
- •Типовые примеры к практическому занятию № 3
- •Типовые примеры к практическому занятию № 4
- •Типовые примеры к практическому занятию № 5
- •Литература
- •420108, Г. Казань, ул. Зайцева, д. 17.
Вариант № 2
1. Если
![]() ,
то модуль
,
то модуль
1) 1; 2) 3; 3) 6;
2. Скалярное
произведение векторов
 и
и
 равно:
равно:
1) -5; 2) 5; 3) -8;
3. Если
 ,
,
 ,
,
 ,
,
 ,
,
 ,
то базис пространства
образуют:
,
то базис пространства
образуют:
1) , , ; 2) , , ; 3) , , ;
4. Линейный оператор
в базисе
,
задан матрицей
 .
Если
.
Если
 ,
то образ
равен:
,
то образ
равен:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
5. Собственные
значения матрицы
 равны:
равны:
1)
![]() ,
;
2)
,
;
3)
,
;
,
;
2)
,
;
3)
,
;
6. Квадратичная
форма
![]() является:
является:
1) Знаконеопределенной; 2) отрицательно определенной;
3) Положительно определенной;
Тест № 2 “Математика” для специальностей экономического профиля |
Указания. Все задания имеют 3 варианта ответа, из которых правильный только один. Запишите на бланке номер выбранного Вами ответа напротив номера задания.
Вариант № 3
1. Если
![]() ,
то модуль
,
то модуль
1)![]() ;
2) 7; 3) 11;
;
2) 7; 3) 11;
2. Скалярное
произведение векторов
 и
и
 равно:
равно:
1) -3; 2) 0; 3) -5;
3. Если
 ,
,
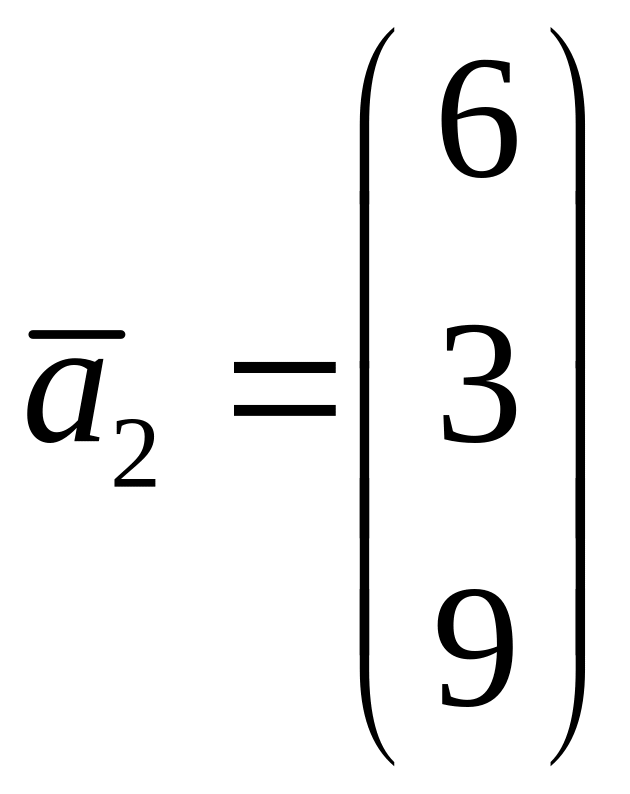 ,
,
 ,
,
 ,
,
 ,
то базис пространства
образуют:
,
то базис пространства
образуют:
1) , , ; 2) , , ; 3) , , ;
4. Линейный оператор
в базисе
,
задан матрицей
 .
Если
,
то образ
равен:
.
Если
,
то образ
равен:
1)
;
2)
;
3)
![]() ;
;
5. Собственные
значения матрицы
 равны:
равны:
1)
,
![]() ;
2)
;
2)
![]() ,
,
![]() ;
3)
;
3)
![]() ,
,
![]() ;
;
6. Квадратичная
форма
![]() является:
является:
1) Знаконеопределенной; 2) отрицательно определенной;
3) Положительно определенной;
Тест № 2 “Математика” для специальностей экономического профиля |
Указания. Все задания имеют 3 варианта ответа, из которых правильный только один. Запишите на бланке номер выбранного Вами ответа напротив номера задания.
Вариант № 4
1. Если
![]() ,
то модуль
,
то модуль
1) 3; 2) 4; 3) 5;
2. Скалярное
произведение векторов
 и
и
 равно:
равно:
1) -1; 2) -2; 3) -3;
3. Если
 ,
,
 ,
,
 ,
,
 ,
,
 ,
то базис пространства
образуют:
,
то базис пространства
образуют:
1) , , ; 2) , , ; 3) , , ;
4. Линейный оператор
в базисе
,
задан матрицей
 .
Если
.
Если
 ,
то образ
равен:
,
то образ
равен:
1)
![]() ;
2)
;
3)
;
2)
;
3)
![]() ;
;
5. Собственные
значения матрицы
 равны:
равны:
1)
,
;
2)
,
;
3)
![]() ,
,
![]() ;
;
6. Квадратичная
форма
![]() является:
является:
1) Знаконеопределенной; 2) отрицательно определенной;
3) Положительно определенной;
Тест № 2 “Математика” для специальностей экономического профиля |
Указания. Все задания имеют 3 варианта ответа, из которых правильный только один. Запишите на бланке номер выбранного Вами ответа напротив номера задания.
Вариант № 5
1. Если
![]() ,
то модуль
,
то модуль
1) 3; 2) 4; 3) 5;
2. Скалярное
произведение векторов
 и
и
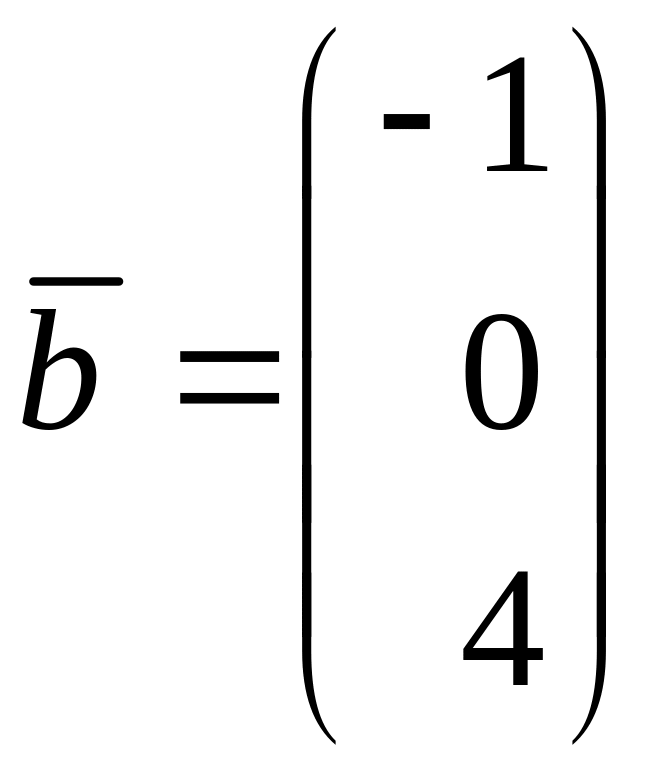 равно:
равно:
1) 1; 2) 2; 3) 3;
3. Если
 ,
,
 ,
,
 ,
,
 ,
,
 ,
то базис пространства
образуют:
,
то базис пространства
образуют:
1) , , ; 2) , , ; 3) , , ;
4. Линейный оператор
в базисе
,
задан матрицей
.
Если
 ,
то образ
равен:
,
то образ
равен:
1)
;
2)
![]() ;
3)
;
;
3)
;
5. Собственные значения матрицы равны:
1) , ; 2) , ; 3) , ;
6. Квадратичная
форма
![]() является:
является:
1) Знаконеопределенной; 2) отрицательно определенной;
3) Положительно определенной;
Тест № 3
Тест № 3 “Математика” для специальностей экономического профиля |
Указания. Все задания имеют 3 варианта ответа, из которых правильный только один. Запишите на бланке номер выбранного Вами ответа напротив номера задания.
