Кривые и поверхности второго порядка Основные теоретические сведения
Общее уравнение второго порядка
является уравнением линии и поверхности. Первые слагаемые этого уравнения представляют квадратичную форму
.
Ортогональным
преобразованием перейдем к новым
переменным и запишем квадратичную форму
в каноническом виде. Затем параллельным
переносом осей координат приведем общее
уравнение к каноническому виду поверхности
второго порядка или кривой, если
.
Множество
точек плоскости
,
удовлетворяющих общему уравнению,
называется кривой второго порядка. В
этом случае каноническое
уравнение может принимать один из
следующих видов:
1)
;
2)
;
3)
.
Примеры решения задач
Задача. Написать каноническое уравнение кривой второго порядка:
.
Решение. Матрица квадратурной части многочлена второй степени равна
.
Характеристический многочлен
.
Собственные
числа матрицы:
;
.
Собственные векторы:
:
,
,
,
так как
.
:
,
,
.
Выполнив
преобразование
,
,
получим:
.
Выделим
полный квадрат по каждой из переменных
и
:
.
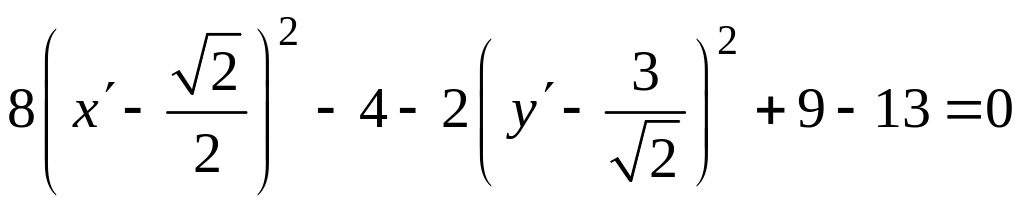Заменой
переменных
,
,
соответствующей сдвигу по каждой из
координатных осей, получим:
или
.
Это каноническое уравнение гиперболы.
Ответ. .
Множество
точек пространства
,
удовлетворяющих общему уравнению,
называется поверхностью второго порядка.
Каноническое уравнение в этом случае
принимает один из следующих видов:
;
;;
;
.
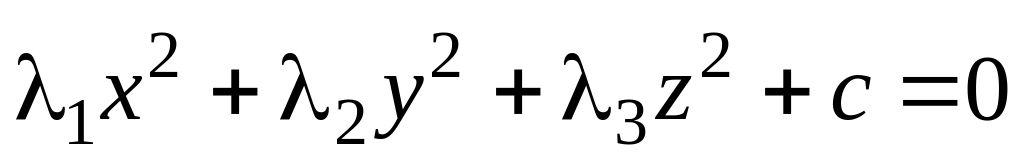
Пример. Написать каноническое уравнение поверхности второго порядка
.
Решение. Матрица квадратурной части многочлена второй степени равна
.
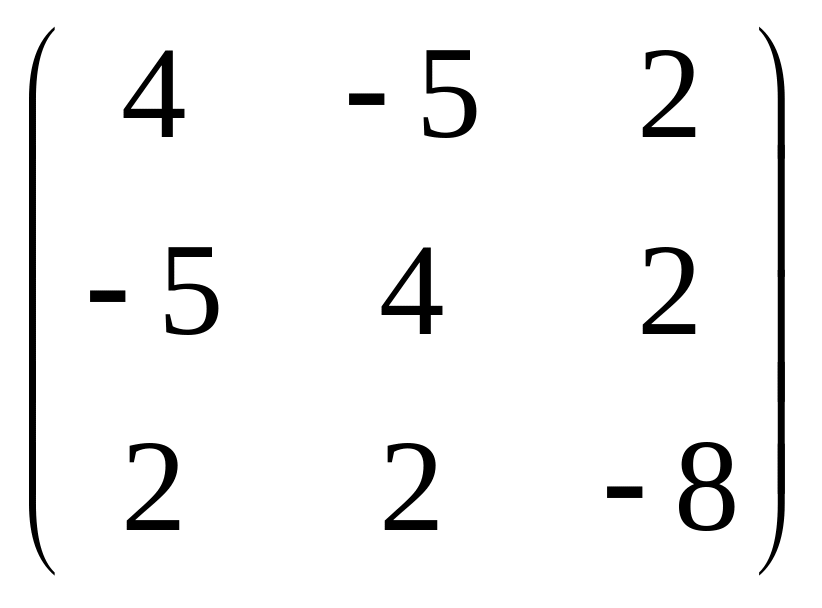Ее
собственные числа:
,
,
,
а собственные единичные векторы:
,
,
.
Выполнив преобразование
,
,
,
получим
.
Преобразование
сдвига выполняем лишь по переменной
:
.
Второе
преобразование координат
,
,
,
окончательно получаем каноническое
уравнение гиперболического параболоида
.
Ответ. .
Задачи для самостоятельного решения
Написать каноническое уравнение кривой второго порядка, определить ее тип:
1.
. Ответ.
Эллипс
.
2.
. Ответ.
Парабола
.
3.
. Ответ.
Гипербола
.
4.
. Ответ.
Эллипс
.
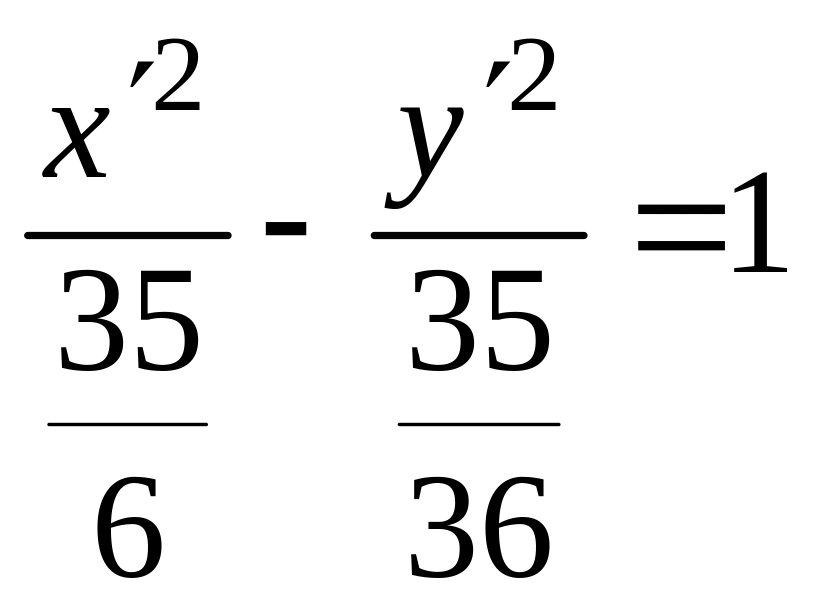5.
. Ответ.
Парабола
.
Написать каноническое уравнение поверхности второго порядка и определить ее тип:
6.
.
Ответ.
Эллипсоид
.
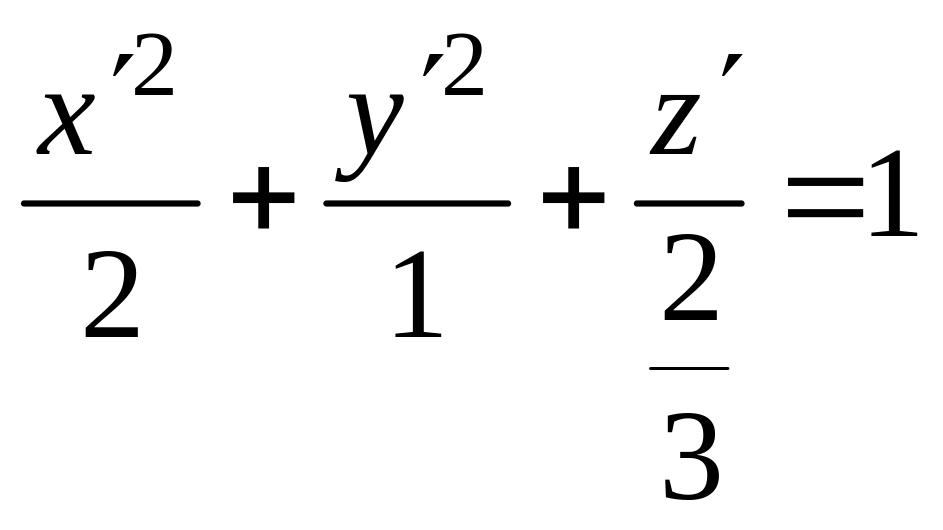7.
.
Ответ.
Гиперболический параболоид
.
8.
.
Ответ.
Двуполостный гиперболоид
.
9.
.
Ответ.
Эллиптический параболоид
.
10.
.
Ответ.
Параболический цилиндр
.
11.
.
Ответ.
Эллиптический цилиндр
.
12.
.
Ответ.
Однополостный гиперболоид
.
Список литературы
1. Исхаков Э.М. Аналитическая геометрия и линейная алгебра: Учебное пособие. Казань: Изд-во Казан. гос. техн. ун-та, 2008. 186 с.
2. Гусак А.А. Задачи и упражнения по высшей математике. В 2 ч. Ч.1. Для вузов. Минск: Высшэйшая шк., 1988. 247 с.
3. Заборская А.П., Хайруллина С.П. Определители и системы линейных алгебраических уравнений. Казань. 1982. 40 с.
4. Амирханова С.Г., Дараган М.А., Дорофеева С.И. Линейная алгебра: Практикум. Казань: Изд-во Казан. гос. техн. ун-та, 2003.–63с.