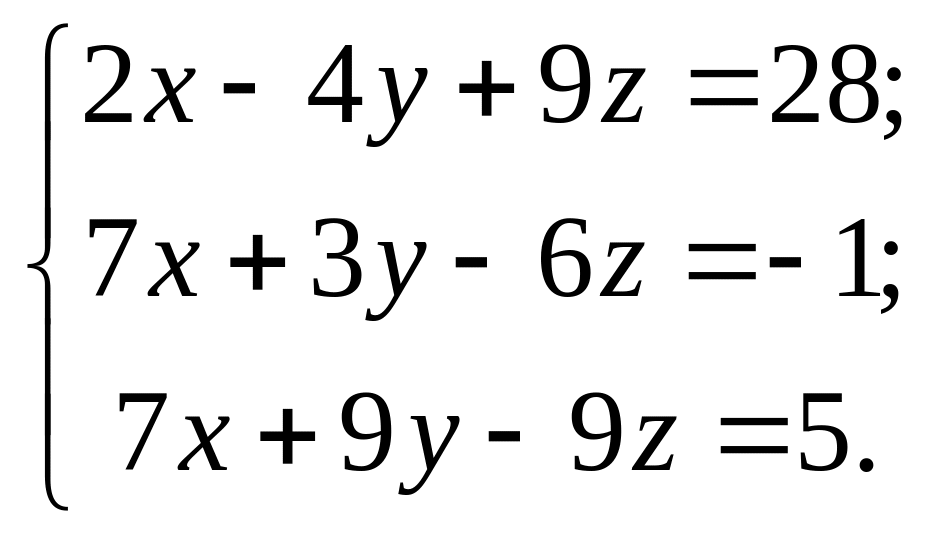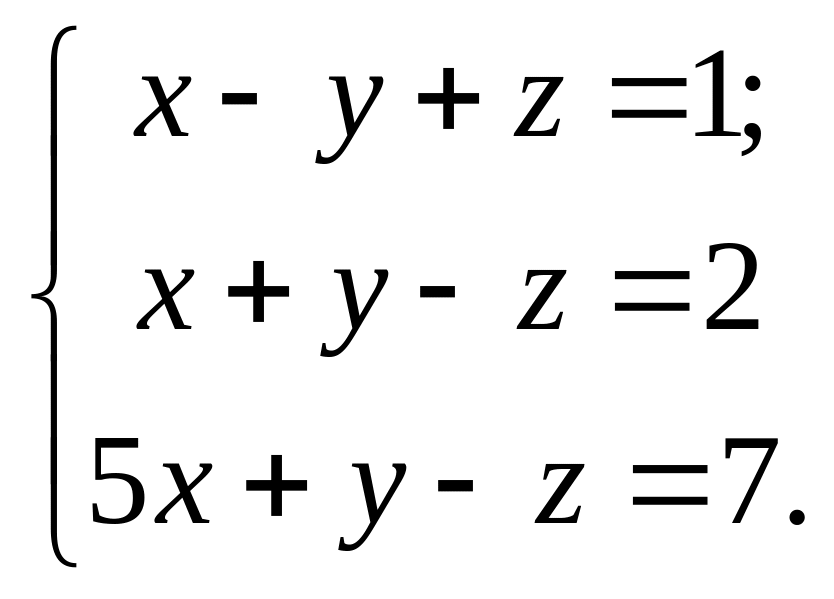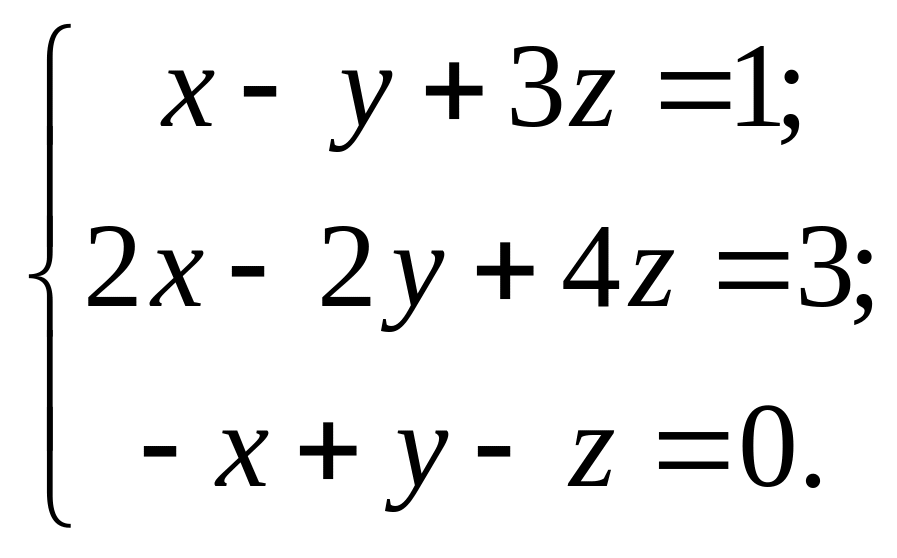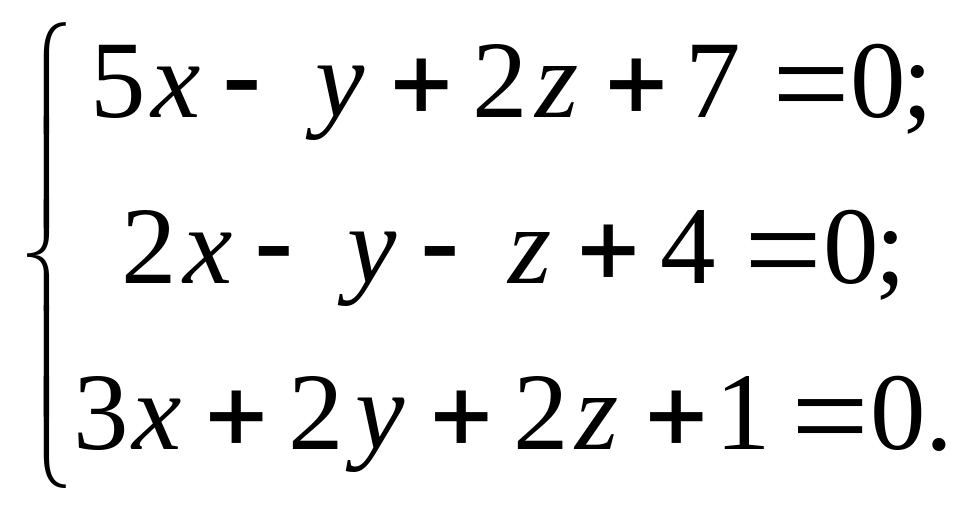- •Определители. Свойства определителей Основные теоретические сведения
- •Основные свойства определителей
- •Приведение определителя к треугольному виду
- •Решение систем уравнений с помощью определителей (по формулам Крамера) Основные теоретические сведения
- •Матрицы. Операции над матрицами Основные теоретические сведения
- •Операции над матрицами
- •Многочлены от матриц
- •Обратная матрица
- •Решение систем алгебраических уравнений методом гаусса Основные теоретические сведения
- •Метод Гаусса. Схема с выбором главного элемента
- •Собственные векторы и собственные значения линейного преобразования Основные теоретические сведения
- •Квадратичные формы
- •Кривые и поверхности второго порядка Основные теоретические сведения
- •Список литературы
- •Оглавление
Приведение определителя к треугольному виду
Определитель
вида
 называется треугольным
(все элементы ниже главной диагонали
равны нулю)
называется треугольным
(все элементы ниже главной диагонали
равны нулю)
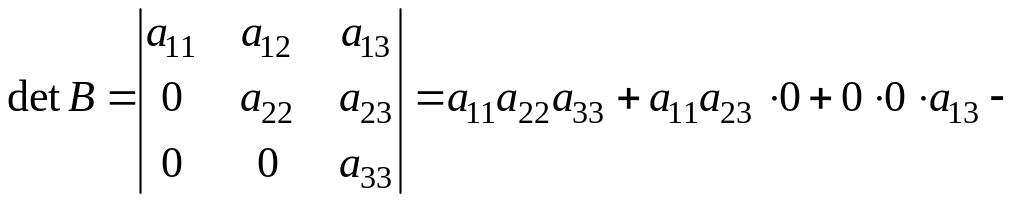
![]() .
.
Треугольный определитель равен произведению элементов главной диагонали.
Определитель, в котором все элементы ниже побочной диагонали, равны нулю, изменением порядка столбцов на обратный сводится к треугольному:
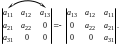
При вычислении иногда удобно, используя свойства определителей 1-6, привести его к треугольному виду и найти произведение элементов главной диагонали.
Решение систем уравнений с помощью определителей (по формулам Крамера) Основные теоретические сведения
Система двух уравнений с двумя неизвестными:
![]()
|
|
![]() ,
,
![]() ,
,
![]() – определитель системы.
– определитель системы.
Определитель
![]() – определитель, полученный заменой
столбца при неизвестном
– определитель, полученный заменой
столбца при неизвестном
![]() на столбец свободных членов.
на столбец свободных членов.
Формулы
Крамера:
![]() ;
;
![]() .
.
Формулы Крамера
 ,
,
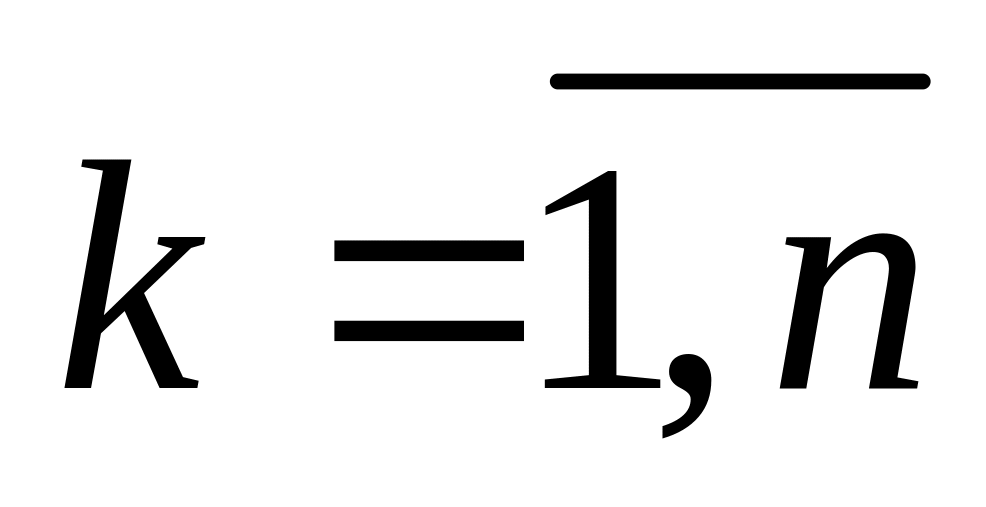 справедливы для систем
линейных уравнений с
неизвестными при условии, что
справедливы для систем
линейных уравнений с
неизвестными при условии, что
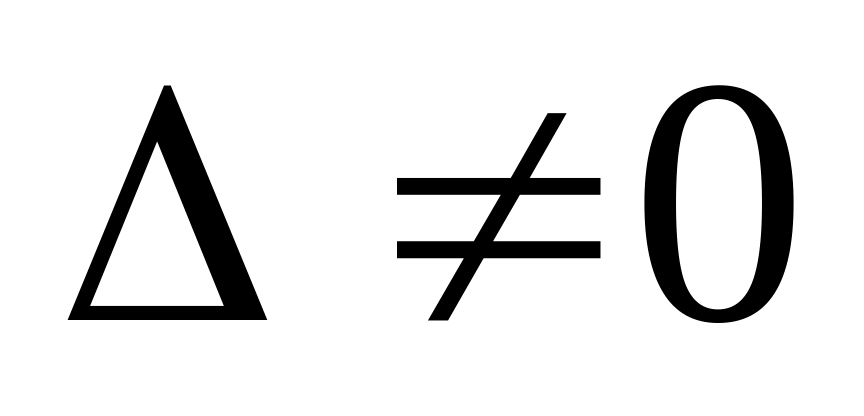 .
.
Если , система имеет единственное решение:
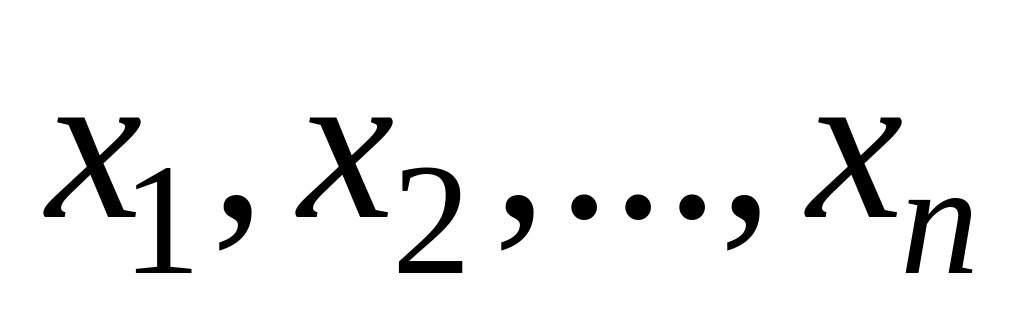 .
.Если
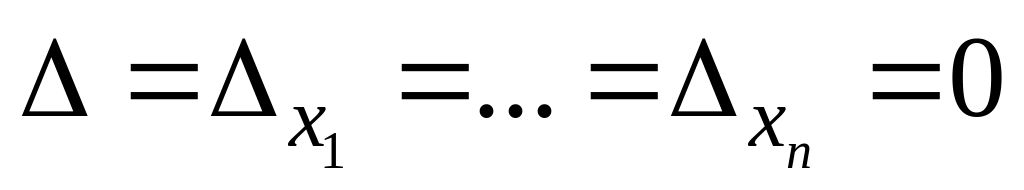 ,
то система имеет множество решений
(эти решения будем искать методом
Гаусса).
,
то система имеет множество решений
(эти решения будем искать методом
Гаусса).Если
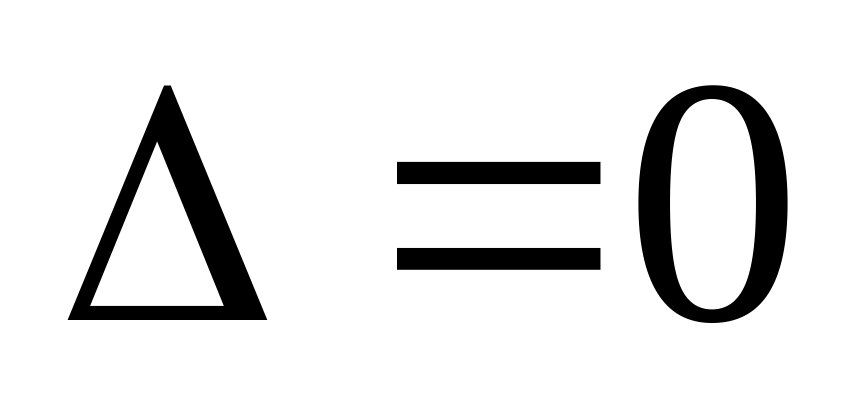 и хотя бы один из определителей
и хотя бы один из определителей
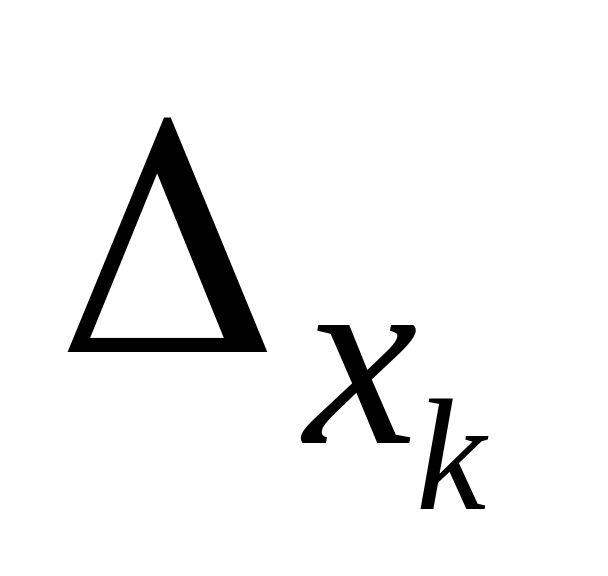 ,
,
отличен от нуля, то система не имеет
решений (несовместна).
,
,
отличен от нуля, то система не имеет
решений (несовместна).
Решение систем из двух уравнений с тремя неизвестными:
![]()
Пусть
![]() ,
тогда систему
,
тогда систему
![]() можно решать по формулам Крамера.
можно решать по формулам Крамера.
Решение системы запишем в виде:
![]() ;
;
![]() ;
;
![]() .
.
Для запоминания порядка коэффициентов при неизвестных нарисуем такую “вертушку”:

Для
неизвестного
![]() – в определители записываем коэффициенты
при
– в определители записываем коэффициенты
при
![]() и
и
![]() ;
для неизвестного
– двигаясь по часовой стрелке, коэффициенты
при
и
;
для неизвестного
– коэффициенты при
и
.
;
для неизвестного
– двигаясь по часовой стрелке, коэффициенты
при
и
;
для неизвестного
– коэффициенты при
и
.
Примеры решения задач
Задача 1. Вычислить определители:
а)

![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Задача 2. Вычислить определитель следующими способами:
а) по правилу треугольников:
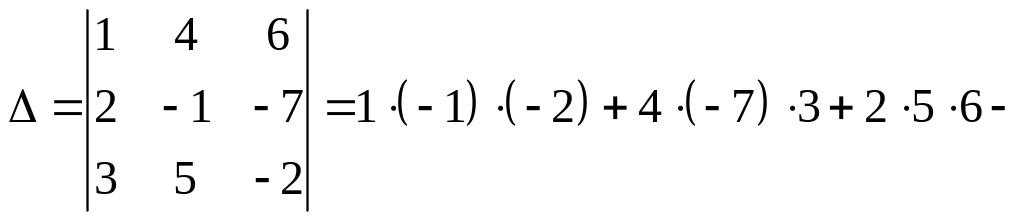
![]() ;
;
б) разложением по первой строке (по определению):
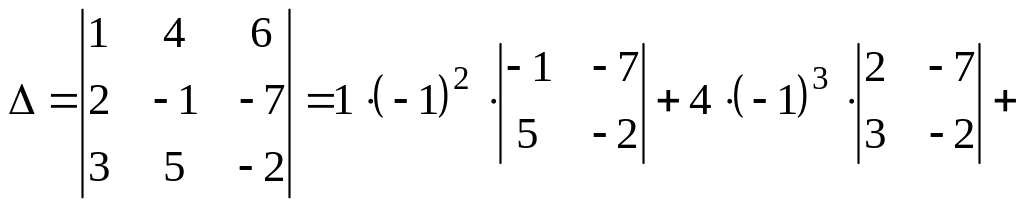
![]() ;
;
в) разложением по второму столбцу:

![]() .
.
Задача 3. Вычислить, используя свойства определителей:
а)
![]()

![]() ;
;
б)
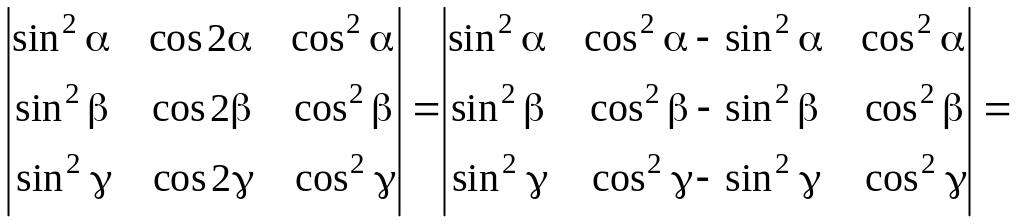
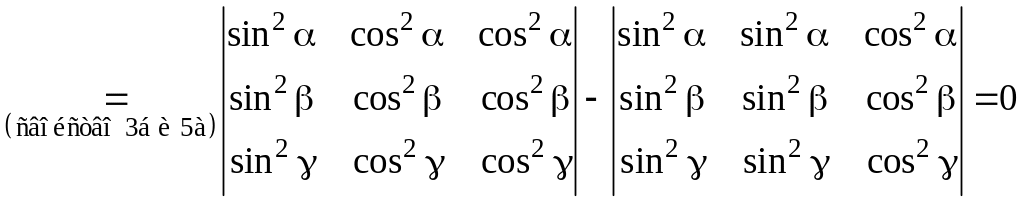 ;
;
в)
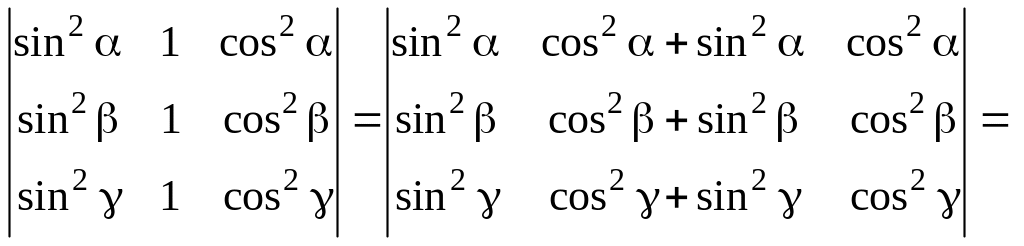
 .
.
Задача
4.
Вычислить определитель Вандермонда и
выяснить, при каких значениях
,
,![]() этот определитель равен нулю:
этот определитель равен нулю:
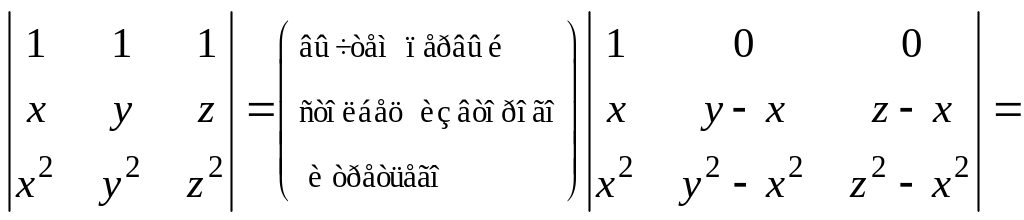
![]()
![]() .
.
Определитель равен нулю при равенстве какой-либо пары чисел из , , .
Задача 5. Доказать, что
а)
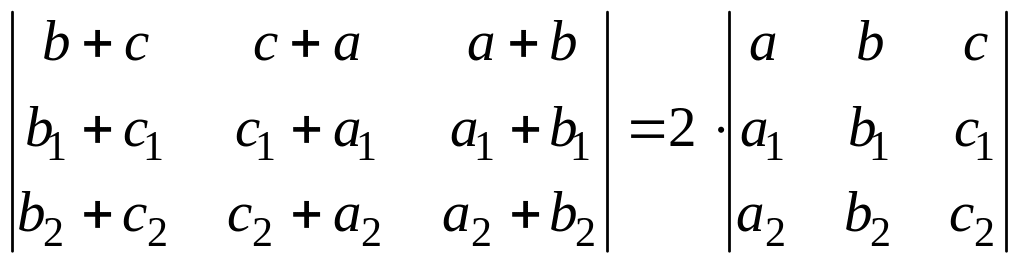 .
.
Решение.
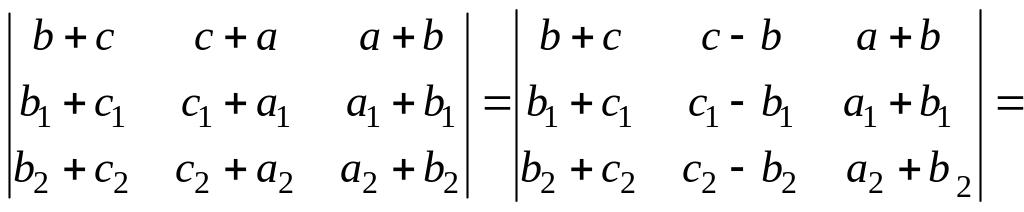
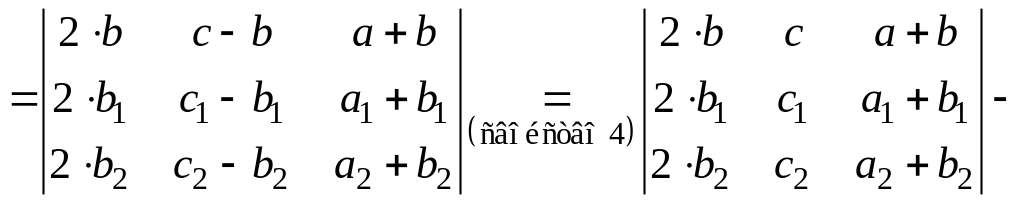
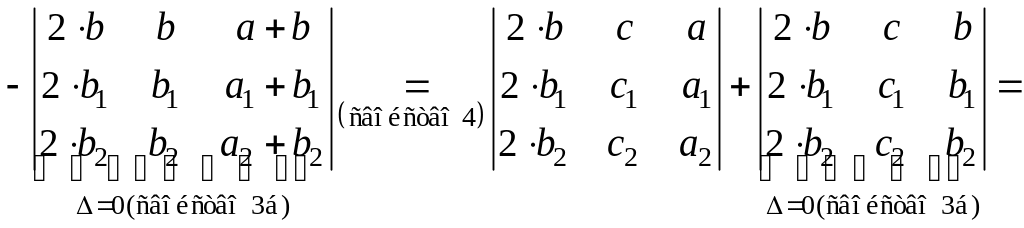
 ;
;
б)
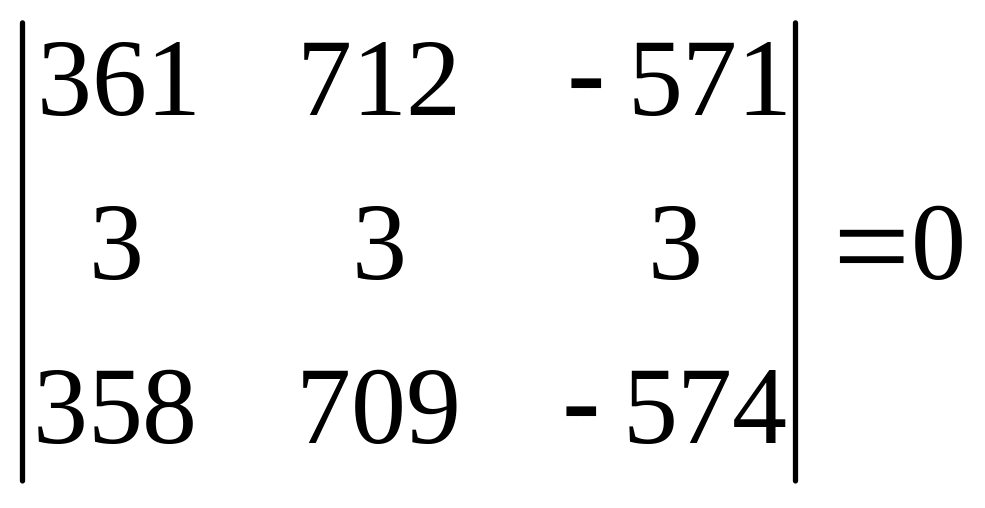 .
.
Решение.
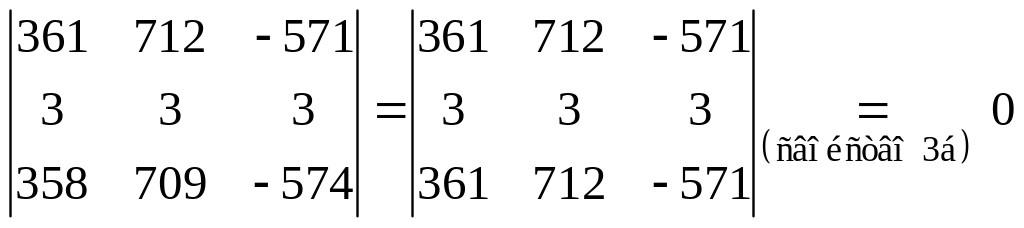 .
.
Задача 6. Решить уравнение:
а)
![]() .
.
Решение.
![]() ,
,
![]() ,
по
теореме Виета:
,
по
теореме Виета:
![]() ,
,
![]() ;
;
б)
 .
.
Решение.
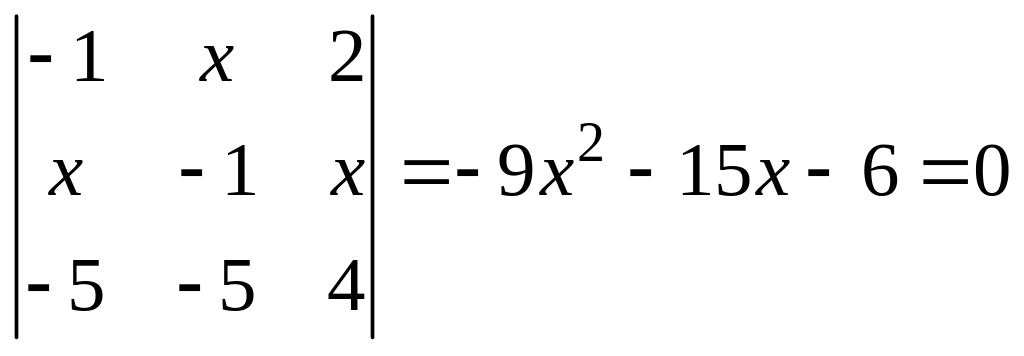 ,
,
![]() ,
,
![]() ,
по
теореме Виета:
,
по
теореме Виета:
![]() ,
,
![]() ;
;
в)
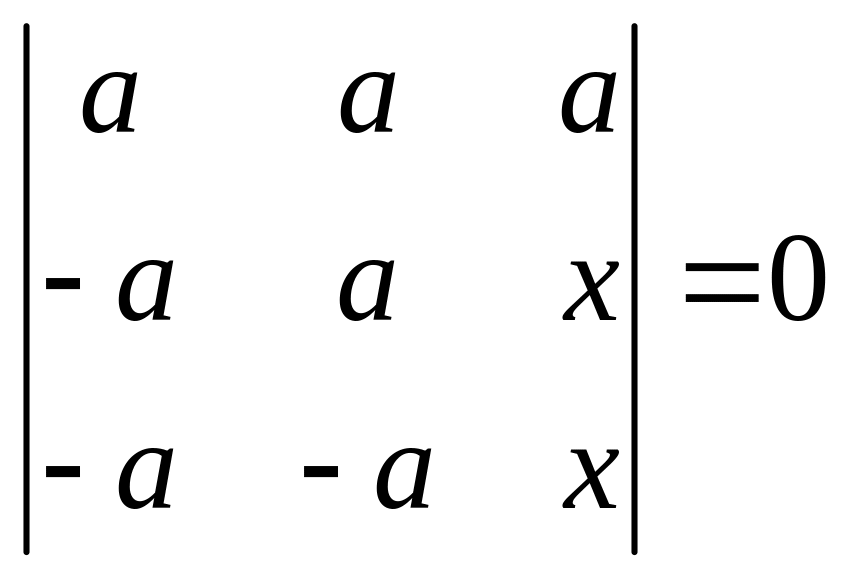 .
.
Решение.
При
![]() определитель равен нулю при любых
.
Если
определитель равен нулю при любых
.
Если
![]() ,
то
,
то
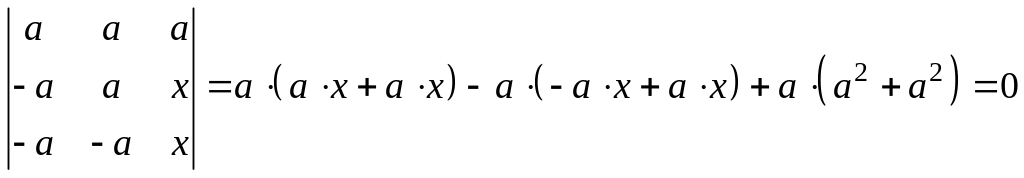 ,
,
![]() ,
,
![]() .
.
Или, преобразуя определитель и складывая первую строку со второй и третьей, получаем
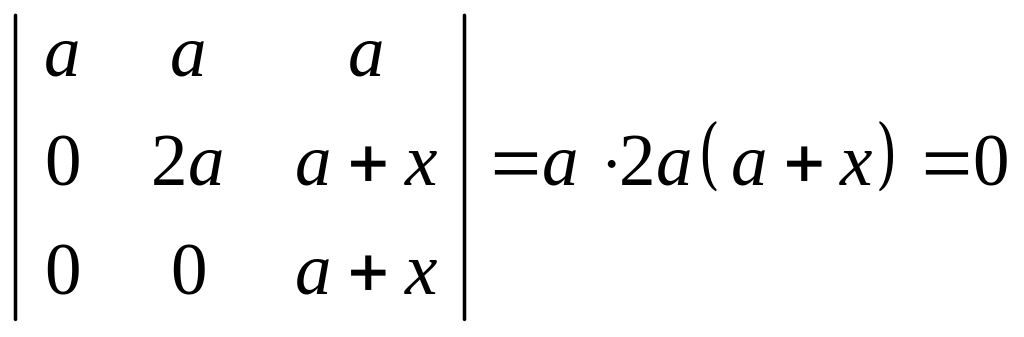 ,
,
![]() .
.
Задача 7. Привести определитель к треугольному виду и вычислить:
1)
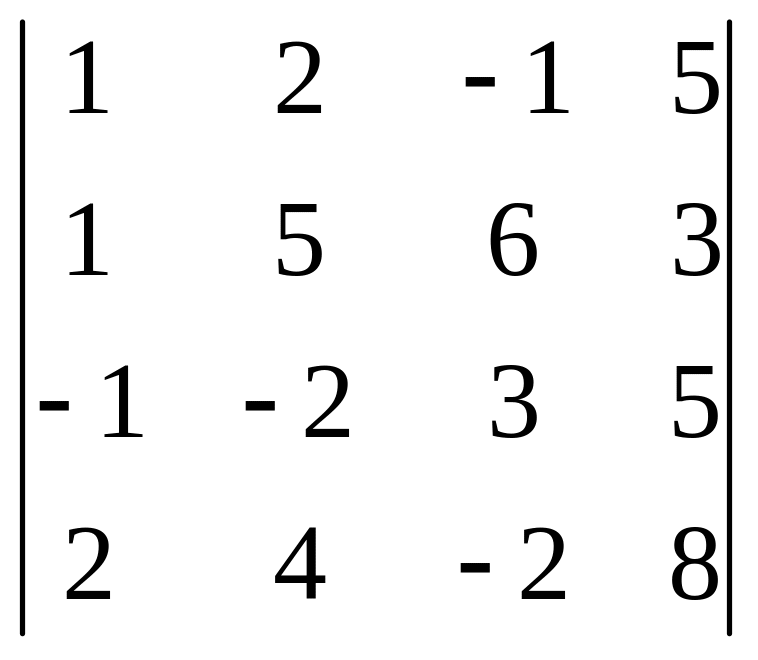 .
.
Решение. Используя свойство линейности, вычтем первую строку из второй, прибавим первую строку к третьей, вычтем первую строку, умноженную на 2, из четвертой
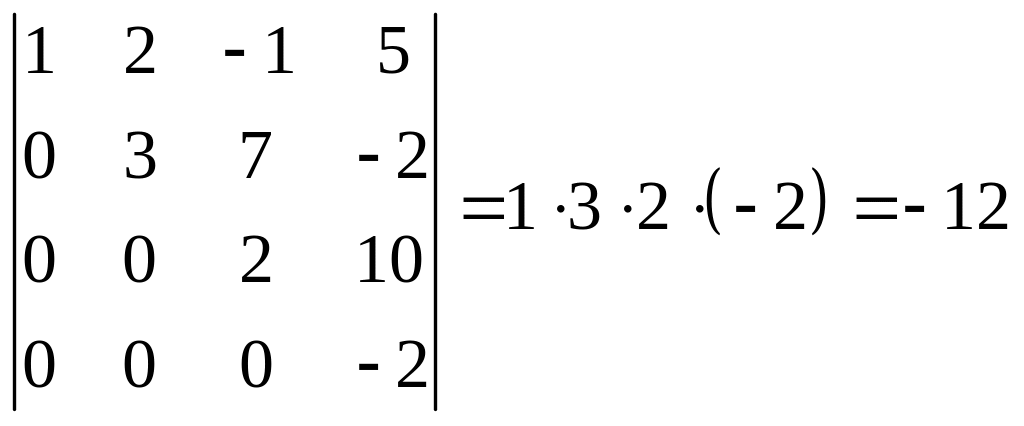 .
.
2)
 .
.
Решение.
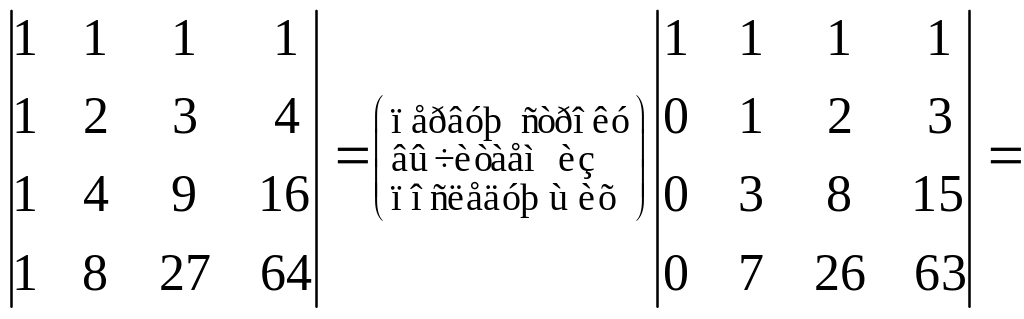
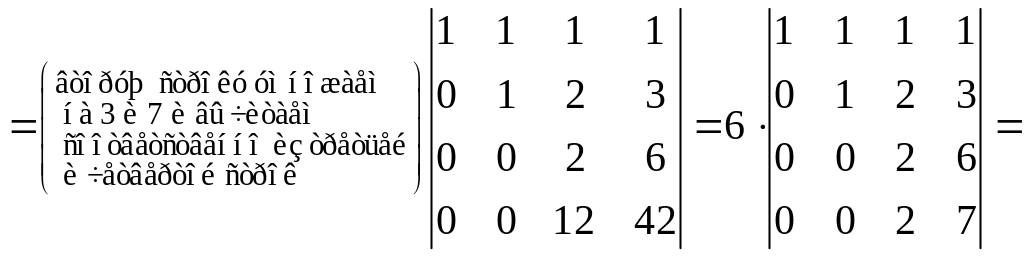
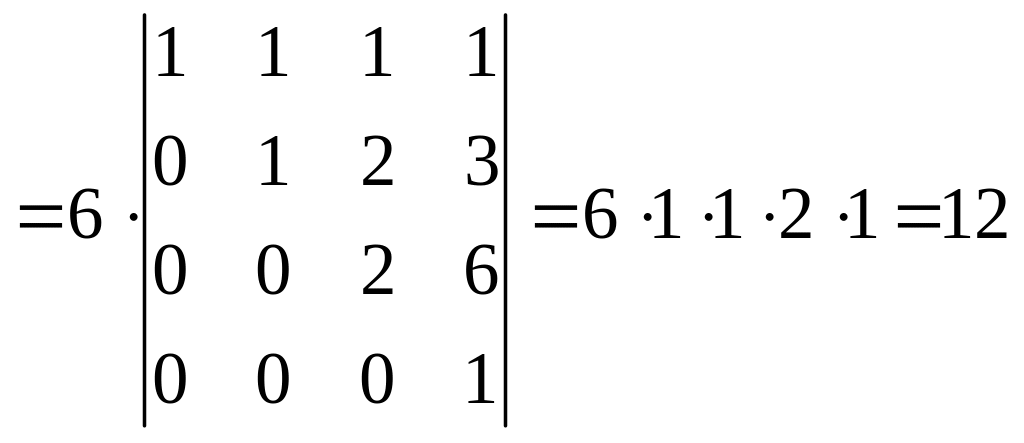 .
.
Задача 8. Вычислить определитель разложением по первой строке (по определению) и какому-либо ряду:
 .
.
а) вычисление определителя разложением по первой строке:
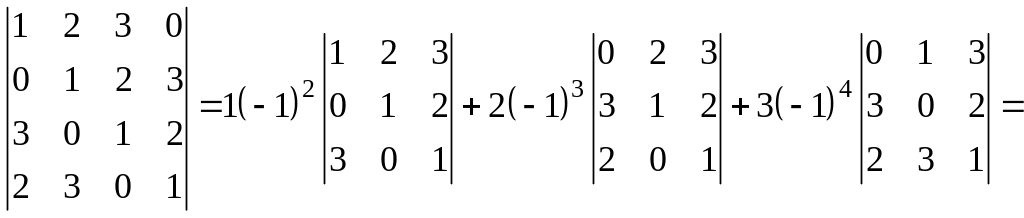
![]()
![]()
![]()
![]() ;
;
б) вычисление определителя по первому столбцу:
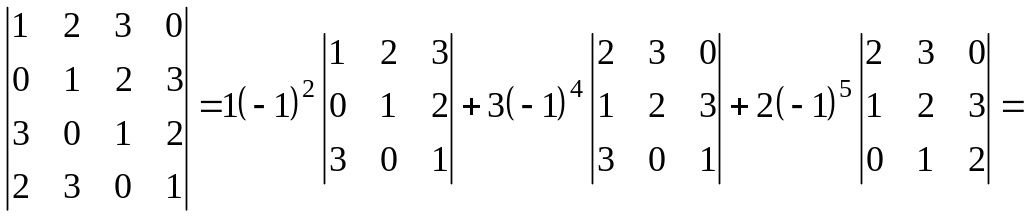

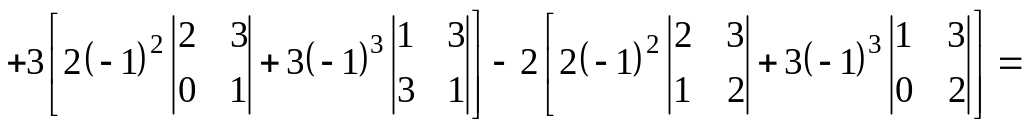
![]()
![]() .
.
Задача 9. Вычислить определители:
а)
 ;
б)
;
б)
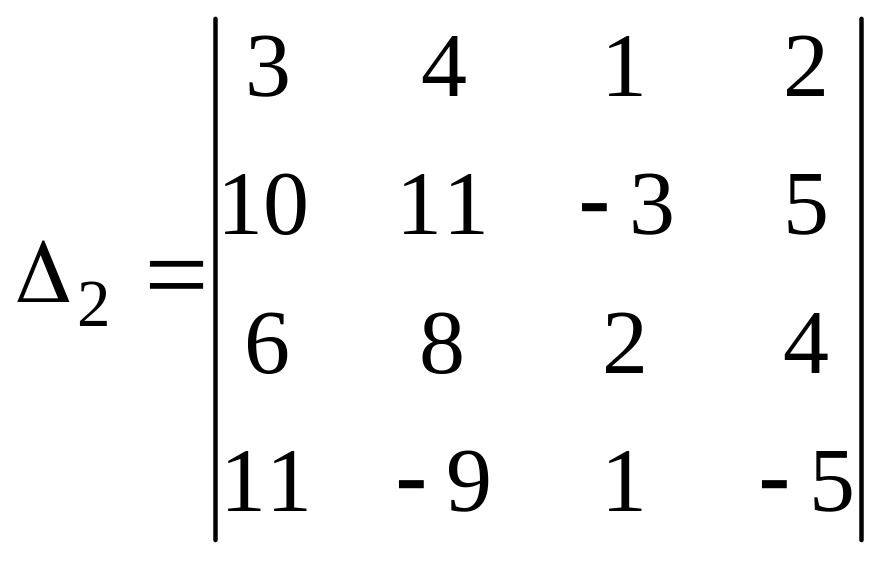 .
.
Решение:
а) применим разложение по четвертой строке:
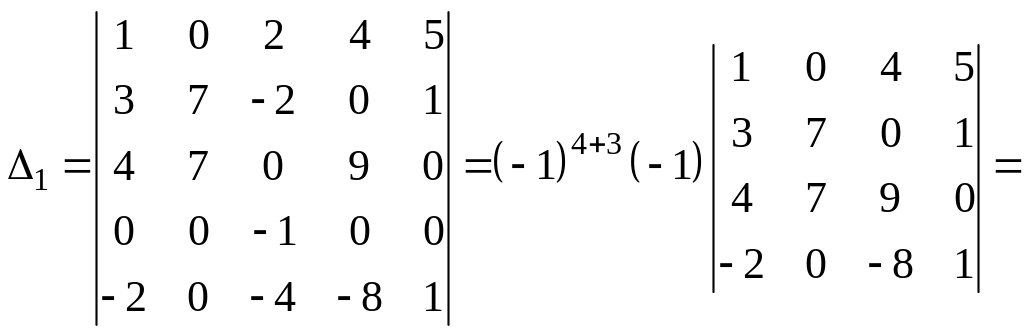

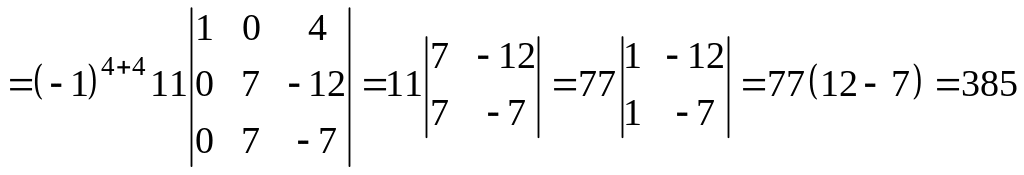 .
.
б) .
Заметим,
что первая и третья строки пропорциональны,
поэтому
![]() .
.
Задача 10. Решить системы:
1)![]()
Решение.
Определитель
данной системы:
![]() отличен от нуля, следовательно, она
имеет единственное решение:
отличен от нуля, следовательно, она
имеет единственное решение:
![]() ,
,
![]() .
.
Таким
образом,
![]() ;
;
![]() ;
;
2)
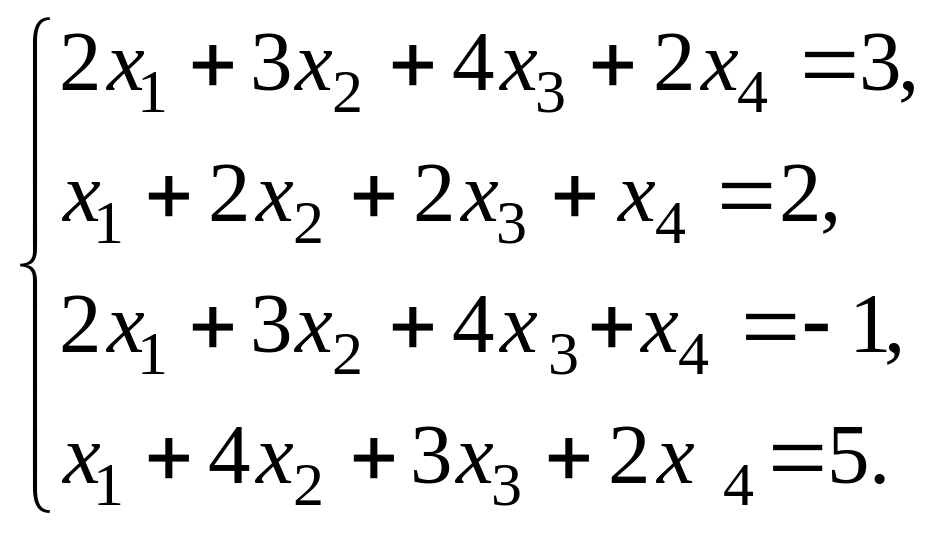
Решение.
Составим определитель системы и вычислим его:
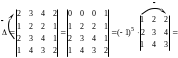
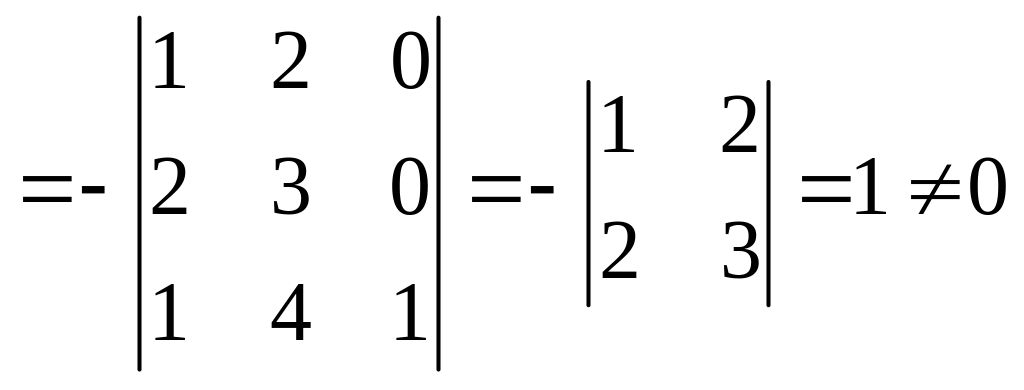 .
.
Определитель , следовательно, формулы Крамера применимы.
Вычислим остальные определители:
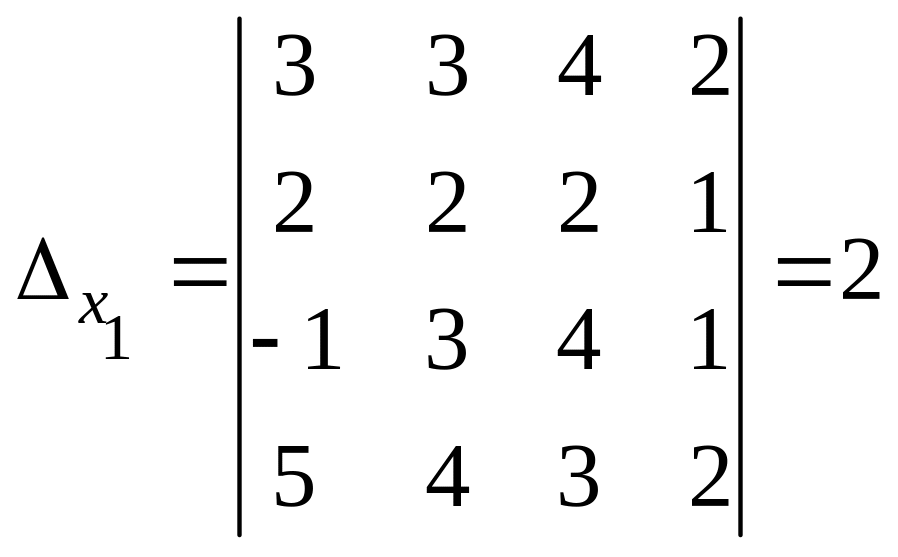 ;
;
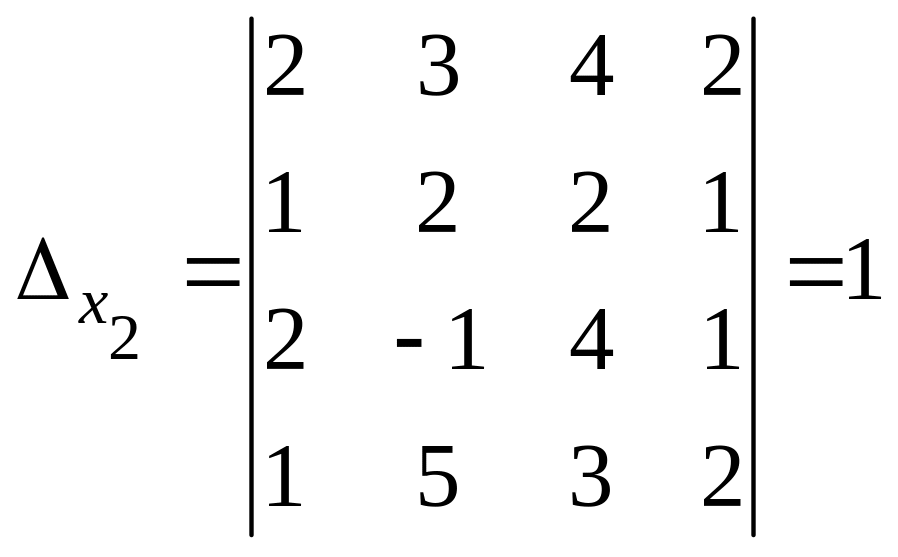 ;
;
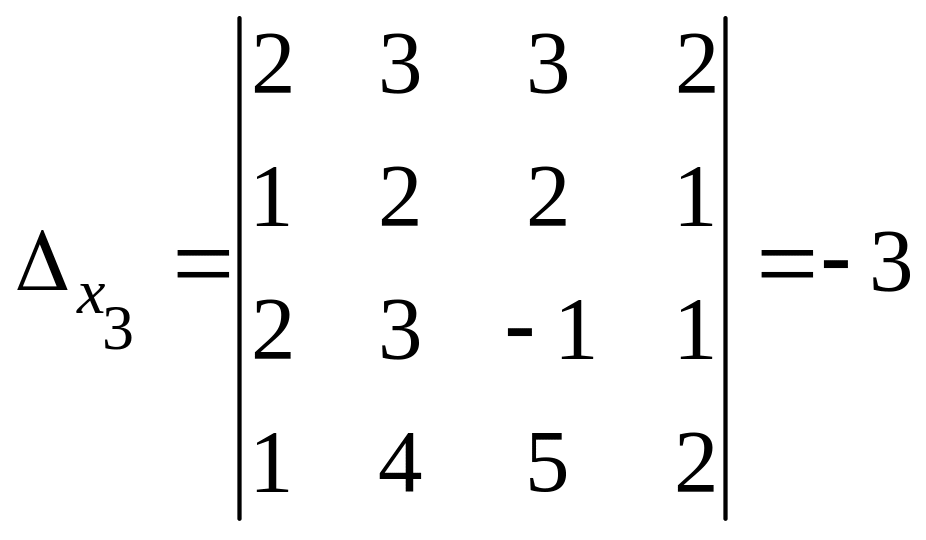 ;
;
 .
.
Итак,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
Проверить постановкой в любое уравнение
системы.
.
Проверить постановкой в любое уравнение
системы.
Задачи для самостоятельного решения
Вычислить определители:
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
Ответ:
1. 144;
2. 1;
3. ![]() ;
4.
;
4. ![]() ;
5. –117;
6. 144;
7. 0;
8. –155;
9.
;
5. –117;
6. 144;
7. 0;
8. –155;
9. ![]() ;
10. 1.
;
10. 1.
Решить систему уравнений:
1. |
2. |
3. |
4. |
5. |
6. |
7. |
|
Ответ: 1. ![]() ;
2. Система
несовместна;
3. Система
несовместна;
4.
;
2. Система
несовместна;
3. Система
несовместна;
4. ![]() ;
5.
;
5. ![]() ,
,
![]() ,
,
![]() ;
6.
;
6. ![]() ,
,
![]() ,
,
![]() ;7.
;7. ![]() .
.

 ,
,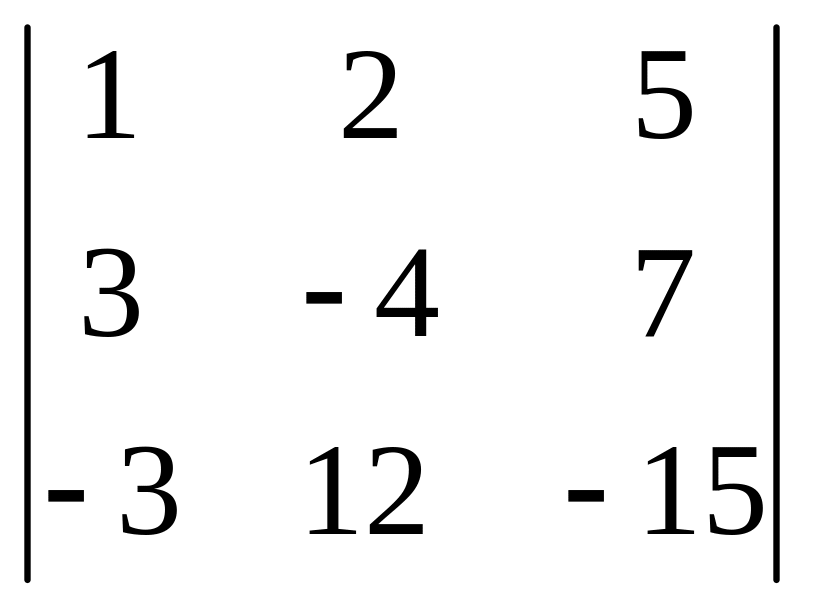 .
.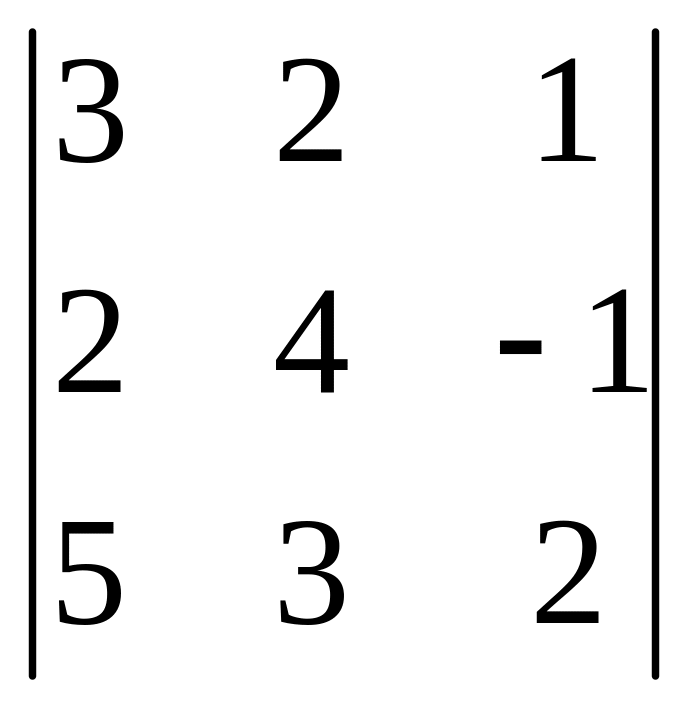 .
.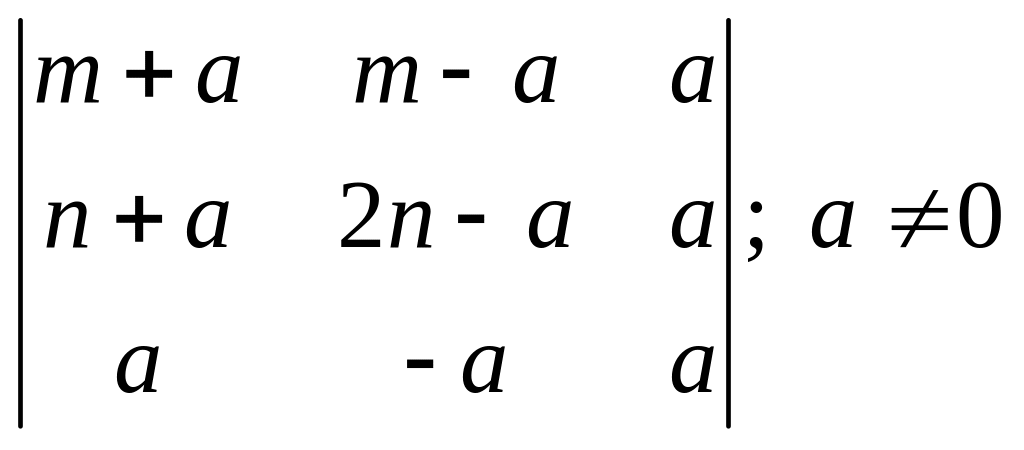 .
. .
. .
. .
.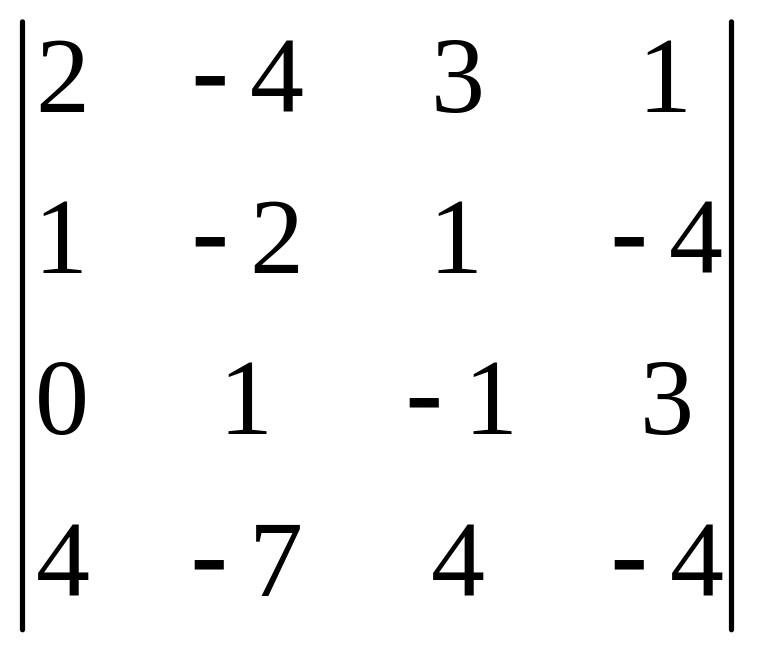 .
.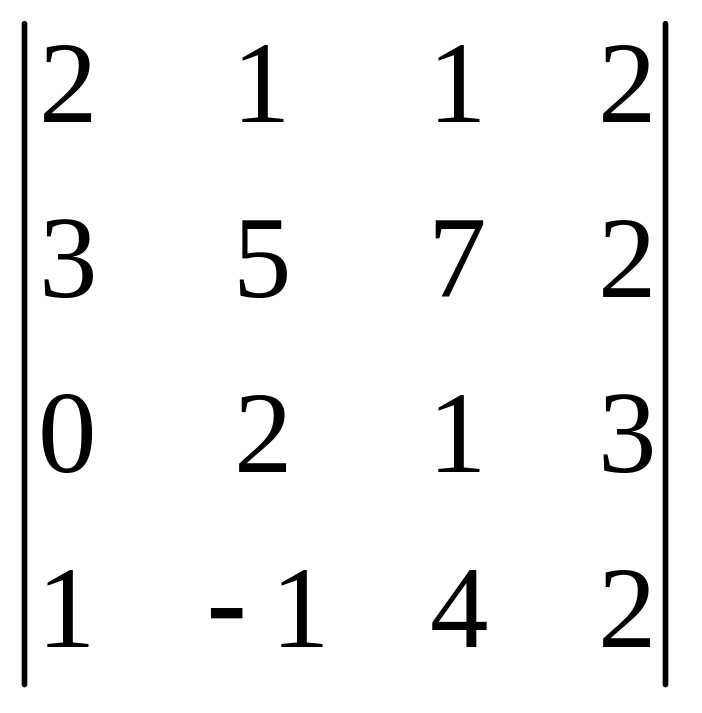 .
.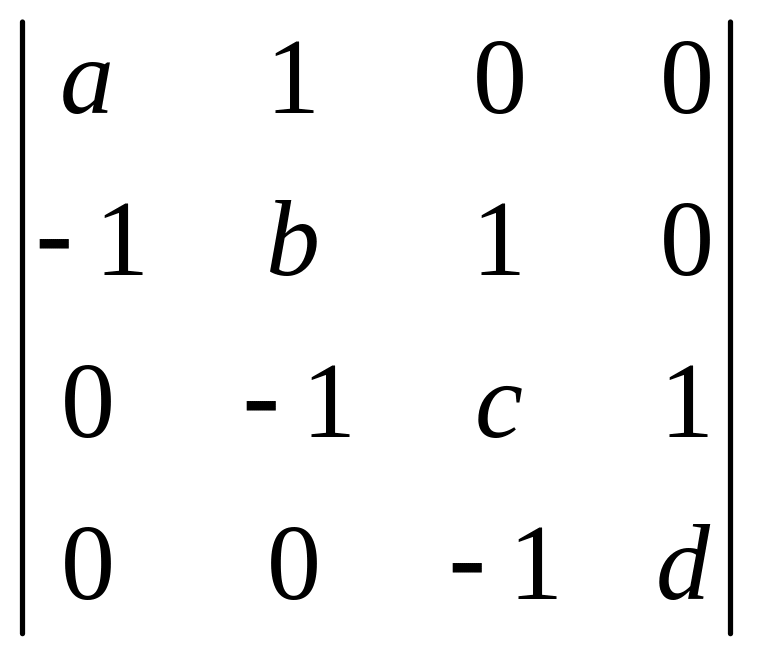 .
. .
.