
5.2. Обедающие философы
Уже классической стала неформальная постановка задачи распределения ресурсов, носящая название "проблемы обедающих философов" и показанная на рисунке 5.1.
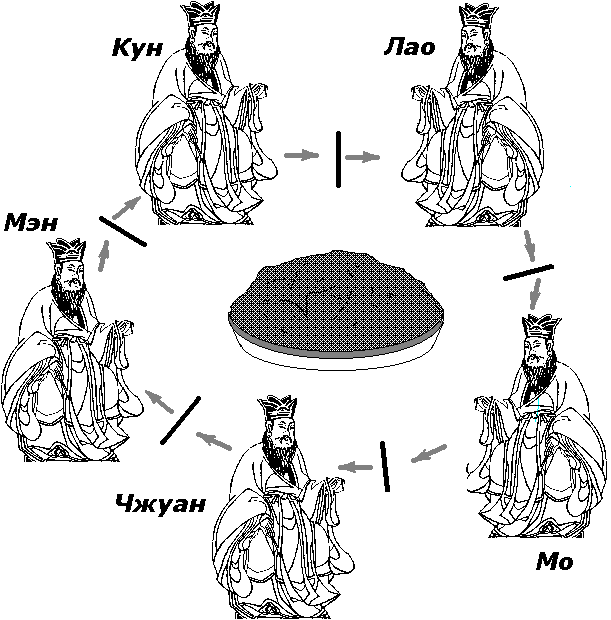
Рисунок 5.1 Обедающие философы. Тупик
Пять философов сидят за круглым столом, в центре которого стоит блюдо с рисом. Между каждой парой философов лежит палочка для еды, палочек, следовательно, тоже пять. Для того, чтобы начать есть, философ должен взять две палочки – слева и справа от себя. Таким образом, если один из философов ест, его соседи справа и слева лишены такой возможности, так как им недостает палочек. Каждый философ "работает" по зацикленному алгоритму: сначала он некоторое время думает, затем берет палочки и ест, затем опять думает и т.д. Временные интервалы мышления и еды случайны, действия философов, следовательно, не синхронизированы. Ничего не говорится в условии о том, каким образом философ берет палочки – наша задача как раз и состоит в том, чтобы обеспечить такую стратегию выделения палочек, которая бы исключала тупики и бесконечное откладывание.
Если мы установим, что каждый философ должен взять одну палочку и не выпускать ее из рук до тех пор, пока не возьмет вторую палочку, то мы можем получить ситуацию, показанную на рисунке 5.1. (Стрелка от философа к палочке означает, что философ хочет взять эту палочку, стрелка в обратном направлении – что эту палочку этот философ уже взял.) Каждый из философов взял палочку справа от себя, но не может взять палочку слева. Ни один из философов не может ни есть, ни думать. Эта ситуация и называется тупиком (deadlock).
Если же мы установим, что философ должен взять обе палочки сразу, то может возникнуть ситуация, показанная на рисунке 5.2. Философ Чжуан хочет взять палочки, но обнаруживает, что его правая палочка занята философом Мо. Чжуан ожидает. Тем временем философ Мэн берет свои палочки и начинает есть. Мо есть заканчивает, но Чжуан не может начать есть, так как теперь занята его левая палочка. Если Мо и Мэн едят попеременно, то Чжуан попадает в положение, которое называется голоданием (starvation) или бесконечным откладыванием.
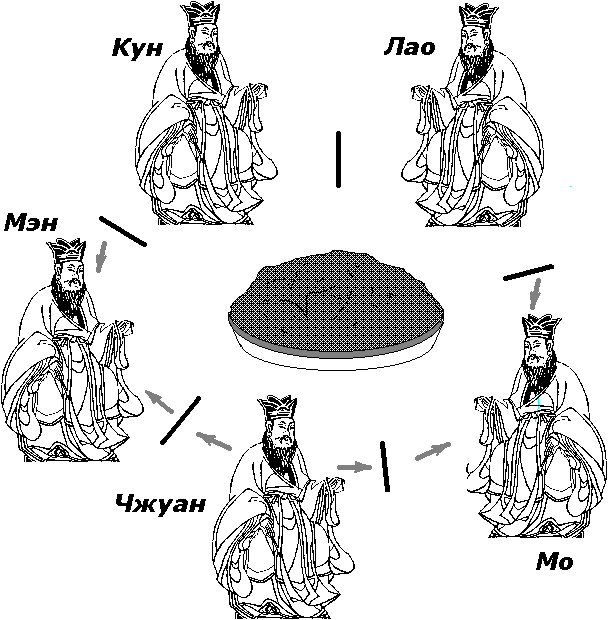
Рисунок 5.2 Обедающие философы. Бесконечное откладывание
Переходя от философов к вычислительным системам, мы можем проиллюстрировать тупик таким примером. Процесс A использует магнитную ленту, но для завершения ему нужен еще и принтер. В это время процесс B удерживает за собой принтер, но ему нужна еще магнитная лента. Процессы A и B блокируют друг друга, то есть находятся в тупике. В системах с множественными ресурсами и с высоким уровнем мультипрограммирования тупиковые ситуации могут быть и не столь очевидными. Тупики могут быть локальными и глобальными. Так, если в приведенном выше примере уровень мультипрограммирования выше 2, то процессы A и B находятся в локальном тупике, другие процессы, которым не требуются ресурсы, занятые процессами A и B, могут выполняться. Философы же на рисунке 5.1 находятся в глобальном тупике.
Бесконечное откладывание – ситуация даже более общая, свойственная управлению любыми ресурсами, а не только монопольными. Так, при планировании процессорного времени по статическим приоритетам низкоприоритетный процесс может откладываться до бесконечности, если в систему постоянно поступают процессы с более высокими приоритетами.
Тупик представляет собой ситуацию более опасную, чем бесконечное откладывание: процессы, попавшие в тупик, удерживают при этом системные ресурсы. Даже если тупик не глобальный, система продолжает работать с уменьшенным объемом ресурсов, следовательно, с пониженной производительностью. Бесконечное же откладывание одного или нескольких процессов может и не повлиять на среднюю пропускную способность системы, но, конечно же, влияет на показатели справедливости обслуживания.
