Решение нулевого варианта контрольной работы

Задание № 1.

Вектор образует с базисными векторами и соответственно, углы и . Определить угол, который образует вектор с вектором .

Решение.

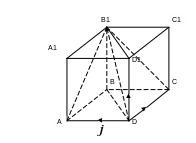
Построим параллелепипед на векторах , , и на диагонали , такой, что векторы и равны.

Тогда в прямоугольном треугольнике с прямым углом , величина угла равна , откуда .

Аналогично в прямоугольном треугольнике с прямым углом величина равна , откуда .

В прямоугольном треугольнике по теореме Пифагора находим:

.

Так как

и

,

то

.

В прямоугольном треугольнике с прямым углом катет , а гипотенуза . Значит, величина угла равна . Но угол равен углу между векторами и . Тем самым задача решена.

Задание № 2.

Заданы три вектора , , в базисе  , , . Доказать, что четырехугольник – плоский. Найти его площадь.

Решение.

1. Если векторы , и компланарные, то – плоский четырехугольник. Вычислим определитель, составленный из координат данных векторов.

.

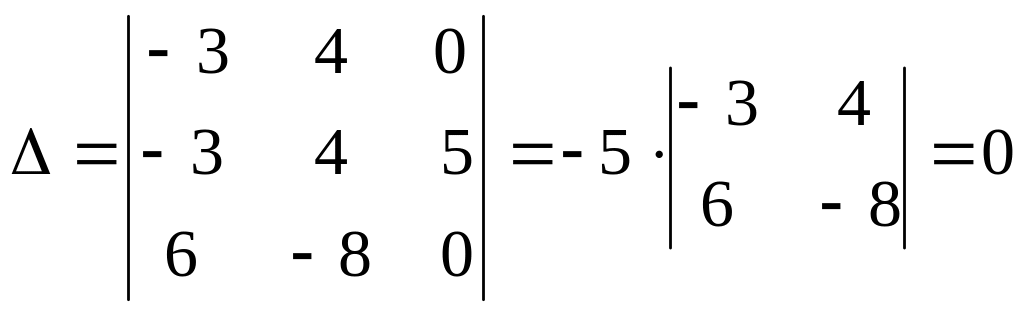Так как определитель равен нулю, то векторы , и компланарные, а значит, четырехугольник – плоский.

2. Заметим, что , поэтому и , таким образом четырехугольник трапеция с основаниями АВ и CD.

D

C

Тогда

.

По свойству векторного произведения имеем:

,

.

Так как

,

то

(0; 0; 5).

Так как

,

то

.

Находим векторное произведение

,

откуда

.

Значит

.

,

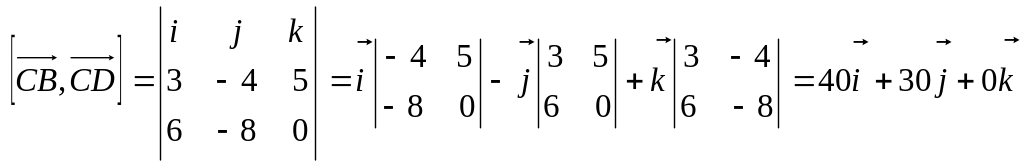откуда

.

Значит

.

Тогда

.

Задание № 3. Найти вектор , коллинеарный вектору (2; 1; –2), у которого длина равна 5.

Решение.

Обозначим координаты вектора (х, у, z). Как известно, у коллинеарных векторов координаты пропорциональны, и поэтому имеем:

х = 2t, y = t, z = − 2t.

По условию задачи | | = 5, а в координатной форме:

.

Выражая переменные через параметр t, получим:

4t² +t² +4t² =25,

откуда

t² = .

Таким образом,

t = 

и

х =  , у =  , z = .

Получили два решения:

₁ ( ; ; − ), ₂ (− ;− ; ).

Тест

Вариант 0.

А 1. Лучи [А, В) и [С, D), лежащие на одной прямой (А, В), называются сонаправленными, если

1) они лежат в одной полуплоскости с границей (А,С)

2) их пересечением является луч; 3) они не пересекаются

4) другой ответ

А 2. Свойство лучей быть противоположно направленными

1) транзитивно 2) симметрично 3) рефлексивно 4) другой ответ

А 3. Вектором в пространстве мы называем

1) отрезок 2) направленный отрезок 3) класс эквиполлентных направленных отрезков 4) другой ответ

А 4. Вычислить определитель

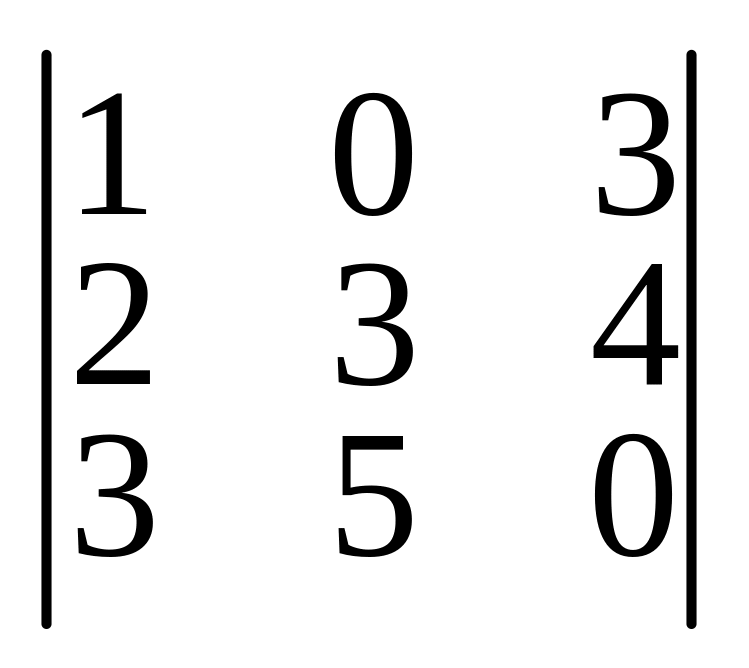
1) 17 2) 16 3) –17 4) 12.

А 5. Найти длину вектора (5, 4, 0)

1) 2) 3) 9 4) другой ответ

А 6. При каком значении векторы и взаимно перпендикулярны?

1) 5 2) – 4 3) 10 4) 4

А 7. Найти сумму , если векторы и коллинеарные

1) 6 2) 18 3) – 6 4) 0

А 8. Если , то векторы и 1) сонаправленые 2) противоположно направленые 3) перпендикулярные 4) равные

А 9. Дано: . Модуль вектора равен 1) 1 2) 3) 4) 5

А 10. Вычислить определитель 1) 1 2) 3 3) –1 4) – 3

А 11. Найти векторное произведение векторов (0; –1; 1). (1; –1; 3)

1) (–2; –1; 1) 2) (–2; 1; 1) 3) (2; 1; 2) 4) другой ответ

А 12. Найти площадь треугольника, построенного на векторах и . 1) 30 2) 15 3) 60 4) другой ответ

А 13. Какая из следующих троек векторов является компланарной?

1) (3; 0; 2), (–5; 3; – 1), (6; 0; 3) 2) (2; 0; 3), (7; 1; 6) , (6; 0; 5) 3) (2; 0; 3), (–1; 7; 2) , (5; –3; 6) 4) (1; –2; 1), (3; 2; 1) , (1; 0; –1)

А 14. Найти вектор , перпендикулярный к векторам (1; 0; 2) и (0; –1; 3) такой, что , и при этом тройка векторов – левая.

1) 2) 3) 4)

А 15. Найти объем параллелепипеда, построенного на векторах

(1; – 2; 1), (3; 2; 1) и (1; 0; –1) 1) 24 2) 10 3) 12. 4) 0

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
отв	2	2	3	3	1	4	3	3	2	1	2	1	3	4	3

Список литературы

1. А.Д. Александров, Н.Ю. Нецветаев. Геометрия. – М.: Наука, 1990.

2. Л.С. Атанасян, В.Т. Базылев. Геометрия. Ч. 1. – М.: Просвещение, 1986.

3. В.Т. Базылев, К.И. Дуничев и др. Геометрия. – Ч. 1. – М.: Просвещение, 1974.

4. В.Т. Базылев, К.И. Дуничев и др. Под ред. В.Т. Базылева. Сборник задач по геометрии. – М.: Просвещение, 1980.

5. Беклемишева Л.А. и др. Сборник задач по аналитической геометрии: Уч.пособие. – М.:, 2003.

6. Бортаковский А.С., Пантелеев А.В. Аналитическая геометрия в примерах и задачах: Учебное пособие. – М.: Высшая школа, 2005.

7. А.Л. Вернер, Б.Е. Кантор, С.А. Франгулов. Геометрия, ч.1.– С. Петербург, 1997.

8. Л.С. Атанасян, В.А. Атанасян. Сборник задач по геометрии. Ч. 1. – М.: Просвещение, 1973.

9. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. – М., 2004. – 464 с.

10. Ефимов Н.В. Высшая геометрия: Учебник для вузов. – М.: Физматлит, 2003. – 584 с.

11. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.1. – Новосибирск: Сиб.унив.изд-во, 2002. – 271 с.

12. Жаферов А.Ф. Геометрия: в 2-х частях. Ч.2. – Новосибирск: Сиб.унив.изд-во, 2003. – 267 с.

13. Кострикин А.И., Манин Ю.И. Линейная алгебра и геометрия. – М.: МГУ, 1980. – 320 с.

14. Д.В. Клетеник. Сборник задач по аналитической геометрии. – М.: Наука, 1964.

15. А.В. Погорелов. Геометрия.– М.: Наука, 1984.

16. О.Н. Цубербиллер. Сборник задач по аналитической геометрии.– М.: Наука, 1966.