Нагрузки на перекрытие (кН/м2)

№ п.п.	Наименование	Нагрузка
		Норматив.	f	Расчетн.
1	2	3	4	5
А	Постоянные:
1	Ламинат δ=12,5мм γ=7.0кН/м3	0.088	1,2	0.105
2	Раствор цем.-песч. δ=20мм γ=18.0кН/м3	0.36	1,3	0.468
4	Керамзитобетон δ=45мм γ=12.0кН/м3	0.54	1,2	0.648
5	Плиты сб. ж/бетон	3.0	1,1	3.30
6	Перегородки (гипсобетон) γ=13.0кН/м3	0.75	1,2	0.90
	Итого:	4.74		5.42
Б	Временные: жилой дом	1.50	1,3	1.95
	Всего:	6.24		7.37

Расчетная нагрузка на 1 пог. м стены от перекрытия составит: q_п= 7.37*5.7/2 = 21.0 кН/м. Расчетная нагрузка от собственного веса кладки q_к= 0.51*(1.8/3)*18*1.1 = 6.06 кН/м. Суммарная нагрузка q= q_п + q_к= 21.0+6.06 = 27.06 кН/м.

Опирание перемычки на кладку стен принимаем по 250 мм в каждую сторону, расчетный пролет L_р= 1800+2*(250/2) = 2050 мм = 2.05 м. При нормальных условиях работы коэффициент условий работы принимается _с =1 [табл. 1, прим. п. 5].

Сечение подбирается исходя из максимального изгибающего момента:

М_мах=q*l²/8 = 27.06•2.05²/8 = 14.21 кНм;

По формуле 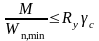, находится W^тр_х=М/(R_у*γ_с)=14.21•10³/(230•10⁶)м³= 61.8•10^-6м³ = 61.8 см³. На один уголок в среднем W^тр_х = 61.8/3 = 20.6 см³.

По сортаменту принимается уголок равнополочный 100*100*8: J_х = 147 см⁴, z₀ = 2.75 см; тогда (b-z₀) = 10/0-2/75 = 7.25см, W_х= J_х/(b-z₀) = 147/7.25 = 20.27см³<20.6 см³, но превышение составляет (20.6-20.27)/20.27*100% = 1.59% <5%, т.е в пределах допустимого.

Подобранное сечение (три уголка равнобоких 100*100*8) удовлетворяет всем заданным условиям.

Пример 3. Подобрать сечение сквозного стержня равноустойчивой сварной центрально сжатой колонны из двух швеллеров, соединенных планками. Расчетная нагрузка от балочного перекрытия F = 1,35 мН. Высота колонны Н = 9м, защемлена внизу и шарнирно закреплена вверху. Материал конструкции - сталь марки С245 с расчетным сопротивлением R_у = 240 МПа [прил. В табл. В.5]. Условия работы – нормальные.

Определяем внутреннее продольное сжимающее усилие, как равное внешней нагрузке, следовательно, N= F = 1,35мН. Коэффициент условий работы _с =0.95 [табл. 1, п. 2]. Тип сечения b (табл. 7). Коэффициент приведения μ при заданном способе закрепления концов стержня равен 0.7 [табл. 30].

Решение. Предварительный подбор сечения. Расчетная длина всего стержня

ℓ_ef = μ Н= 0,7•9 м = 6,3 м.

Практика расчета стальных центрально сжатых сквозных колонн показывает, что целесообразно задаваться значением = 0,7...0,9. Требуемая площадь сечения одного швеллера при  = 0,85: А≥ N/(2_*_*R_у*_с) = 1,35 10⁶/(2*0,85 * 240 10⁶) м² = 33,1 10^-4 м² = 33,1 см².

По сортаменту принимается швеллер 27У с площадью сечения А =35,2 см² > 33,1см²; J_х =4160см⁴; J_уо =262см⁴; i_х =10,9см; i_уо =2,73 см; х_с=2,47 см.

Проверка принятого сечения на устойчивость относительно оси х.

Эту ось часто называют материальной, поскольку она пересекает ветви колонны. Гибкость сквозного стержня относительно указанной оси равна гибкости одной ветви (швеллера) относительно той же оси.

Следовательно, λ_х = ℓ_х /i_х = ℓ_ef/ i_х=630/10,9 =58

условная гибкость = λ* = 58*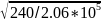 = 1.98; коэффициент продольного изгиба по табл. [прил. Д, табл. Д.1]  = 0,826;

Напряжения в колонне Ϭ =N/(*2*А*_с)= 1,35• 10⁶/(0,826* 2* 35,2• 10^-4*0.95) Па =

= 244• 10⁶ Па = 244 МПа > R_у = 240 МПа, но превышение напряжения составляет (244-240)/240*100% = 1.6% <5%, т.е в пределах допустимого.

Проверка принятого сечения на устойчивость относительно оси у.

Исходя из равноустойчивости сечения требуется определить расстояние между наружными гранями полок швеллеров. Момент инерции всего сечения относительно оси у должен быть не меньше момента инерции относительно оси x: J_у≥2* J_х = 2*4160 = 8320 см⁴

Момент инерции всего сечения относительно оси у: J_у = 2* J_у1+2* А₁а², отсюда расстояние от центра всего сечения до центра тяжести ветви «а» составит:

а= = = 10.52 см.

В этом случае расстояние между наружными гранями полок швеллеров составит:

В = 2*(а+ х_с) = 2*(10.52+2.47) = 25.98 см ≈ 260 мм

Пример 4. Подобрать поперечное сечение прокатной двутавровой балки перекрытия, шарнирно опертой по краям, проверить ее прочность на сдвиг и прогиб. Условия работы — нормальные. Расчетный пролет балки – 6м; нормативная равномерно распределенная нагрузка – 33.62кН/м; расчетная равномерно распределенная нагрузка – 38.67кН/м.

Решение. Задаемся сталью марки С245. Расчетное сопротивление стали растяжению (сжатию) при изгибе R_у = 240 МПа [прил. В табл. В.5], сдвигу R_s=140 МПа [табл.2 R_s = 0,58R_yn/γ_m]. Модуль упругости для стали Е=2.06*10⁵ Н/мм² [прил. Г, табл. Г.10]. При нормальных условиях работы коэффициент условий работы принимается _с =1 [табл. 1, прим. п. 5].

Сечение подбирается исходя из максимального изгибающего момента

М_мах=ql²/8 = 38,67•6²/8 = 174кНм

По формуле , находится W^тр_х=М/(R_у*γ_с)=174•10³/(240•10⁶) м³ = 725•10^-6 м³= 725 см³.

По сортаменту принимается двутавр 35Б1: W_х= 774.8см³>725см³.

Так как подобранное сечение требуется проверить на сдвиг, из сортамента выбираются данные, необходимые для подсчета наибольших касательных напряжений: S_х = 434 см³; J_х = 13 560см⁴; s = 0,7 см (толщина стенки двутавра, в сортаменте обозначенная- «s», в формуле СНиПа-«t»).

Расчет производится по максимальной поперечной силе Q= ql/2=38,67•6/2=116кН

Пользуясь условием τ = QS/Jt и, полагая t=s,

τ_мах =116•10³•434•10^-6/(13560•0,7•10^-10)=53,0•10⁶Па=53,0 МПа< R_s=140 МПа,

следовательно, стенка имеет значительный запас прочности на сдвиг.

Проверка прогиба.

Для определения его числового значения необходимо воспользоваться упрощенными формулами; расчет ведем по 2-му предельному состоянию.

f= 5q_нℓ⁴/384ЕJ - для балки на двух опорах.

f = 5•33.62•6⁴/384•206•10⁶ •1.356•10^-4 = 0.0203м=2.03см

где: q_н=33.62 кН/м; Е=206 ГПа=206•10⁶ кН/м²; ℓ=6м; J_х = 13 560см⁴=1,356•10^-4м⁴

Предельный прогиб по [прил. Е, табл. Е.1] составляет

f_u=1/200ℓ=6/200=0,03м=3см>f=2.03см

Подобранный номер двутавра удовлетворяет всем заданным условиям.

Пример 5. Определить несущую способность (предельное загружение равномерно распределенной нагрузкой) прокатного двутавра 35Б1 с учетом деформаций прогиба. Условия работы — нормальные. Балка перекрытия пролетом – 6м шарнирно опертая по концам.

Решение. Задаемся сталью марки С245. Расчетное сопротивление стали растяжению (сжатию) при изгибе R_у = 240 МПа [прил. В табл. В.5]. Модуль упругости для стали Е = 206 ГПа [прил. Г, табл. Г.10]. При нормальных условиях работы коэффициент условий работы принимается _с =1 [табл. 1, прим. п. 5].

Для двутавра 35Б1 по сортаменту W_х= 641.3см³, J_х = 11 095см⁴.

По формуле , находится М = W_х R_у=641.3•10⁶•240•10⁶=153912Нм=153.91кНм

Так как М_мах=ql²/8, то q=8М/ l²=8•153.91/6²=34.20 кН/м

Проверка прогиба аналогична, приведенному в примере 4.

Необходим учет усредненного коэффициента γ_f=1,15 при переходе к расчетам по 2-му предельному состоянию.

f= 5qℓ⁴/384ЕJ γ_f - для балки на двух опорах.

f= 5•34.2•6⁴/384•206•10⁶ •1.1095•10^-4•1.15=0,0220м=2,2см

где q=34.2кН/м; Е=206 ГПа=206•10⁶ кН/м²; ℓ=6м; J_х = 11 095см⁴=1,1095•10^-4м⁴

Предельный прогиб по [прил. Е, табл. Е.1] составляет

f_u=1/200ℓ=6/200=0,03м=3см>f=2,2см

Принятый номер двутавра удовлетворяет всем заданным условиям.

Пример 6. Определить несущую способность (предельное загружение сосредоточенной силой) центрально сжатой стальной колонны из прокатного двутавра 45Б1. Высота колонны Н — 8 м, концы в направлении главных плоскостей защемлены. Условия работы — нормальные. Сталь марки С245. Расчетное сопротивление стали растяжению (сжатию) при изгибе R_у = 240 МПа [прил. В табл. В.5]. При нормальных условиях работы коэффициент условий работы принимается _с =1 [табл. 1, прим. п. 5].

Решение. Тип сечения b (табл. 7). Коэффициент приведения μ при заданном способе закрепления концов стержня равен 0,5 [табл. 30]. Из сортамента для двутавра 45Б1 i_min = i_У = 4.33 см, А = 84,3 см².

Определяем по формуле λ =ℓ_р / i_min ═ μ Н /i_У=0,5•800/4.33 = 92 < 150, где

λ_пр ═ 150 – предельная гибкость колонны по [табл. 32],

μ - коэффициент приведения при заданном способе закрепления концов стержня равен 0,5 [табл. 30].

Условная гибкость = λ* = 92* = 3.14; по табл. [прил. Д, табл. Д.1] = 0,614; из формулы напряжения Ϭ =N/( А)≤ R_у_с определяется N=R_у_с А

=240•10⁶*1*0.614*84,3•10^-4=1242245Н=1242.24кН

Следовательно, несущая способность колонны составляет 1242.24кН

46